本文主要是介绍Codeforces Round #210 (Div. 1) A. Levko and Array Recovery,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
A. Levko and Array Recovery
Levko loves array a1, a2, ... , an, consisting of integers, very much. That is why Levko is playing with array a, performing all sorts of operations with it. Each operation Levko performs is of one of two types:
- Increase all elements from li to ri by di. In other words, perform assignments aj = aj + di for all j that meet the inequation li ≤ j ≤ ri.
- Find the maximum of elements from li to ri. That is, calculate the value
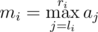 .
.
Sadly, Levko has recently lost his array. Fortunately, Levko has records of all operations he has performed on array a. Help Levko, given the operation records, find at least one suitable array. The results of all operations for the given array must coincide with the record results. Levko clearly remembers that all numbers in his array didn't exceed 109 in their absolute value, so he asks you to find such an array.
Input
The first line contains two integers n and m (1 ≤ n, m ≤ 5000) — the size of the array and the number of operations in Levko's records, correspondingly.
Next m lines describe the operations, the i-th line describes the i-th operation. The first integer in the i-th line is integer ti (1 ≤ ti ≤ 2) that describes the operation type. If ti = 1, then it is followed by three integers li, ri and di (1 ≤ li ≤ ri ≤ n, - 104 ≤ di ≤ 104) — the description of the operation of the first type. If ti = 2, then it is followed by three integers li, ri and mi (1 ≤ li ≤ ri ≤ n, - 5·107 ≤ mi ≤ 5·107) — the description of the operation of the second type.
The operations are given in the order Levko performed them on his array.
Output
In the first line print "YES" (without the quotes), if the solution exists and "NO" (without the quotes) otherwise.
If the solution exists, then on the second line print n integers a1, a2, ... , an (|ai| ≤ 109) — the recovered array.
Examples
input 4 5 1 2 3 1 2 1 2 8 2 3 4 7 1 1 3 3 2 3 4 8 output YES 4 7 4 7 input 4 5 1 2 3 1 2 1 2 8 2 3 4 7 1 1 3 3 2 3 4 13 NO
题意:有两种操作,第一种操作是将l到r之间的数加d;第二种操作是求l到r间的最大值
现在已知操作的情况,问你原始的序列是怎么样的。是否存在。存在输出YES并输出序列,否则输出NO。
解法:构造。
这类题目可以被归在思维、或者说是构造的题目里。
第一次见到确实无从下手,不知道是什么做法。
那么思路是我们要想办法去满足这个序列的操作2也就是最大值的限制。
因此我们可以先构造一个每个数都是inf(1e9)的序列,然后反向操作。
遇到操作2的则把对应区间里超过d的数改为d
遇到操作1就相应减就可以了。
然后再正向操作一遍看是否正确。
这样看似没有问题了,但还是wa了两次。
是因为题目要求ai绝对值小于1e9,但是存在在加的过程中数字超过1e9的情况。
只需要把大于1e9的改成1e9即可。
#include<bits/stdc++.h>using namespace std;
typedef long long int ll;
const int maxn = 2e4 + 10;
const int oo = 1e9;
int a[maxn], b[maxn];
struct node
{int t, l, r, d;
};
node q[maxn];
int main()
{ios::sync_with_stdio(false);cin.tie(0);int m, n;cin >> n >> m;for(int i = 1; i <= n; i++)a[i] = oo;for(int i = 0; i < m; i++)cin >> q[i].t >> q[i].l >> q[i].r >> q[i].d;for(int i = m - 1; i >= 0; i--){if(q[i].t == 1){for(int j = q[i].l; j <= q[i].r; j++)a[j] -= q[i].d;}else{for(int j = q[i].l; j <= q[i].r; j++)if(a[j] > q[i].d)a[j] = q[i].d;}}int flag = 1;for(int i = 1; i <= n; i++){b[i] = a[i];b[i] = b[i] > oo ? oo : b[i];a[i] = b[i];}for(int i = 0; i < m; i++){if(q[i].t == 1){for(int j = q[i].l; j <= q[i].r; j++)a[j] += q[i].d;}else{int mmax= -oo - 1;for(int j = q[i].l; j <= q[i].r; j++)if(a[j] > mmax)mmax = a[j];if(mmax != q[i].d){flag = 0;break;}}}if(flag){cout << "YES" << endl;for(int i = 1; i <= n; i++)cout << b[i] << ' ';cout << endl;}else cout << "NO" << endl;return 0;
}
这篇关于Codeforces Round #210 (Div. 1) A. Levko and Array Recovery的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





