本文主要是介绍PSINS中的各类更新代码解析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1、姿态更新
更新原理
微分方程
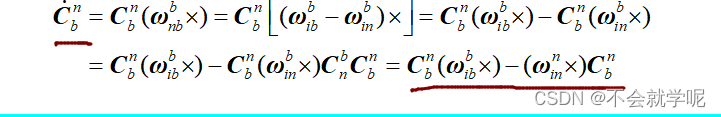
因为离散化比较复杂,所以采用矩阵链转换
更新也就是找到前后时刻的关系。下面是推导逻辑,

PSINS中的涉及到的代码
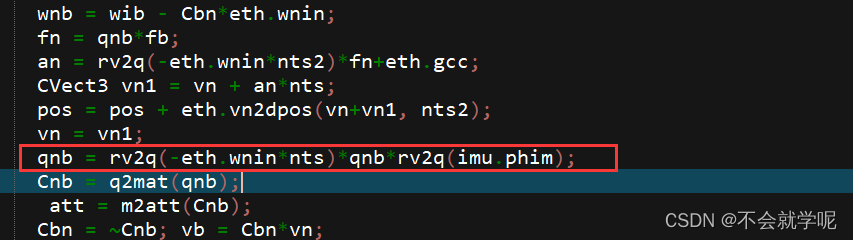
需要注意的是叫增量采用的增量时刻不同,n系下是用【T/2,T】的姿态表示【T,2T】的姿态变化;所以rv2q()中使用的是T/2时刻的角速率*T/2 代表【T/2,T】的角增量-eth.wnin*nts。
b下的角增量直接用的是ins更新的时候【0 T】的角增量imu.phim。
2、速度更新
比力方程

既然是时间相关的更新,对速度微分积分,t-1 ----t的积分

所以速度更新的问题就变成了求解比力产生的速度增量,以及有害加速度产生的速度增量。
有害加速度,一般认为因为其引起的导航坐标系旋转和重力矢量变化都是很小的,所以在计算时间内,选择中间时刻的值代表整个时间段的值,因次可以直接用有害加速度gcc*时间差dt,得到有害加速度产生的速度增量。

那么比力的速度增量,其实按照严老师的讲义,此处省略。
小角模型

实际编码中,是先将dt (上式的T)时间段的速度增量已经得到了,对应的代码中的imu.dvbm,注意是b系下的比力的速度增量,通过下式,速度增量/时间 == 速度变化率,也就是平均加速度,得到dt时间段内的fb,

然后利用
fn = qnb*fb; 这一行代码是b下的加速度转到n下,但是这里的qnb其实上 qn(t-1)b(t-1)
那么原则上fn(t)应该是下式中的表达式,代码实际上是没有第三个Cb(t-1)(t)的矩阵的,fb已经用的是均值了上面已经求解了,所以不存在所谓的b下的旋转,用了fb平均。
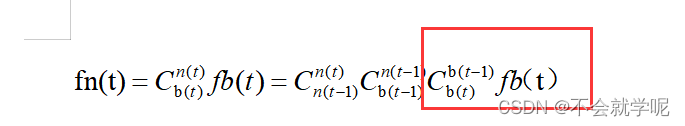
an = rv2q(-eth.wnin*nts2)*fn+eth.gcc; 转换后的n下的fn+有害加速度gcc 得到最终的加速度an
an = rv2q(-eth.wnin*nts2)*qnb*fb + eth.gcc
然后n下的速度增量求出
vn1 = vn + an*nts;
对比公式和代码,发现公式是用速度增量直接表达,而代码中用的是加速度和时间的关系去表达,所以这里框住的速度增量其实就是imu.dvbm,
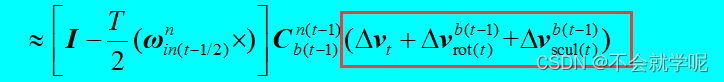
(rv2q(-eth.wnin*nts2)*qnb*fb *dt 与上图是等价的,fb *dt 就是上图框住的增量。
3、位置更新
微分方程
![]()
时间积分
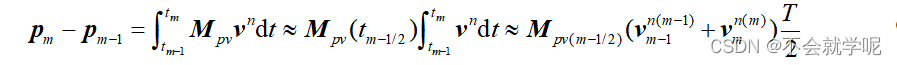
系数矩阵MPv用1/2时刻代替(在地球参数更新的时候可得到),速度是求两个时刻的速度求均值,然后位置增量再乘以T,合起来就是上式中的T/2
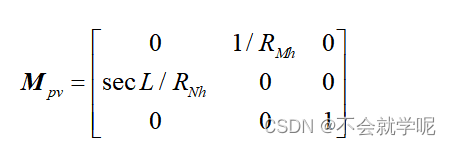
对应的代码
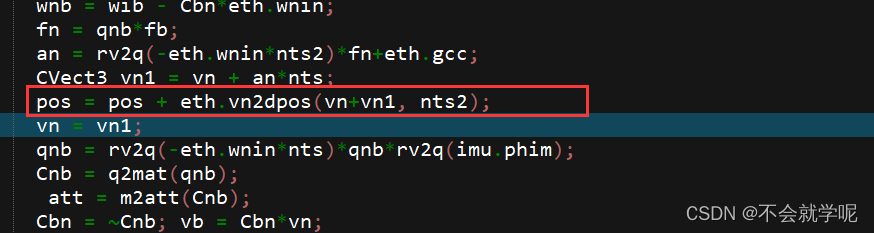
这篇关于PSINS中的各类更新代码解析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




