本文主要是介绍python数据分析常用图大集合,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
- 一、折线图
- 二、直方图
- 三、垂直条形图
- 四、水平条形图
- 五、饼图
- 六、箱线图
- 七、热力图
- 八、散点图
- 九、蜘蛛图
- 十、二元变量分布
- 十一、面积图
- 十二、六边形图
以下默认所有的操作都先导入了numpy、pandas、matplotlib、seaborn
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns一、折线图
石头文学 www.10tou.com折线图可以用来表示数据随着时间变化的趋势
x = [2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019]
y = [5, 3, 6, 20, 17, 16, 19, 30, 32, 35]- Matplotlib
plt.plot(x, y)
plt.show()
- Seaborn
df = pd.DataFrame({'x': x, 'y': y})
sns.lineplot(x="x", y="y", data=df)
plt.show()
二、直方图
直方图是比较常见的视图,它是把横坐标等分成了一定数量的小区间,然后在每个小区间内用矩形条(bars)展示该区间的数值
a = np.random.randn(100)
s = pd.Series(a) - Matplotlib
plt.hist(s)
plt.show()
- Seaborn
sns.distplot(s, kde=False)
plt.show()
sns.distplot(s, kde=True)
plt.show()

三、垂直条形图
条形图可以帮我们查看类别的特征。在条形图中,长条形的长度表示类别的频数,宽度表示类别。
x = ['Cat1', 'Cat2', 'Cat3', 'Cat4', 'Cat5']
y = [5, 4, 8, 12, 7]- Matplotlib
plt.bar(x, y)
plt.show()
- Seaborn
plt.show()
四、水平条形图
x = ['Cat1', 'Cat2', 'Cat3', 'Cat4', 'Cat5']
y = [5, 4, 8, 12, 7]
plt.barh(x, y)
plt.show()
五、饼图
nums = [25, 37, 33, 37, 6]
labels = ['High-school','Bachelor','Master','Ph.d', 'Others']
plt.pie(x = nums, labels=labels)
plt.show()
六、箱线图
箱线图由五个数值点组成:最大值 (max)、最小值 (min)、中位数 (median) 和上下四分位数 (Q3, Q1)。
可以帮我们分析出数据的差异性、离散程度和异常值等。
- Matplotlib
# 生成0-1之间的10*4维度数据
data=np.random.normal(size=(10,4))
lables = ['A','B','C','D']
# 用Matplotlib画箱线图
plt.boxplot(data,labels=lables)
plt.show()
- Seaborn
# 用Seaborn画箱线图
df = pd.DataFrame(data, columns=lables)
sns.boxplot(data=df)
plt.show()
七、热力图
力图,英文叫 heat map,是一种矩阵表示方法,其中矩阵中的元素值用颜色来代表,不同的颜色代表不同大小的值。通过颜色就能直观地知道某个位置上数值的大小。
flights = sns.load_dataset("flights")
data=flights.pivot('year','month','passengers')
sns.heatmap(data)
plt.show()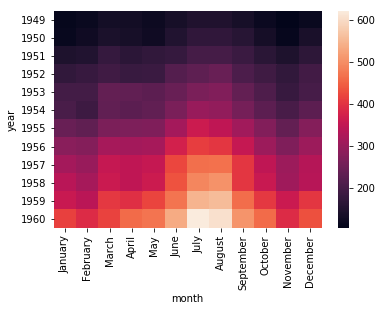
通过 seaborn 的 heatmap 函数,我们可以观察到不同年份,不同月份的乘客数量变化情况,其中颜色越浅的代表乘客数量越多
八、散点图
散点图的英文叫做 scatter plot,它将两个变量的值显示在二维坐标中,非常适合展示两个变量之间的关系。
N = 1000
x = np.random.randn(N)
y = np.random.randn(N)- Matplotlib
plt.scatter(x, y,marker='x')
plt.show()
- Seaborn
df = pd.DataFrame({'x': x, 'y': y})
sns.jointplot(x="x", y="y", data=df, kind='scatter');
plt.show()
九、蜘蛛图
蜘蛛图是一种显示一对多关系的方法,使一个变量相对于另一个变量的显著性是清晰可见
labels=np.array([u"推进","KDA",u"生存",u"团战",u"发育",u"输出"])
stats=[83, 61, 95, 67, 76, 88]
# 画图数据准备,角度、状态值
angles=np.linspace(0, 2*np.pi, len(labels), endpoint=False)
stats=np.concatenate((stats,[stats[0]]))
angles=np.concatenate((angles,[angles[0]]))
# 用Matplotlib画蜘蛛图
fig = plt.figure()
ax = fig.add_subplot(111, polar=True)
ax.plot(angles, stats, 'o-', linewidth=2)
ax.fill(angles, stats, alpha=0.25)
# 设置中文字体
font = FontProperties(fname=r"/System/Library/Fonts/PingFang.ttc", size=14)
ax.set_thetagrids(angles * 180/np.pi, labels, FontProperties=font)
plt.show()
十、二元变量分布
二元变量分布可以看两个变量之间的关系
tips = sns.load_dataset("tips")
tips.head(10)
#散点图
sns.jointplot(x="total_bill", y="tip", data=tips, kind='scatter')
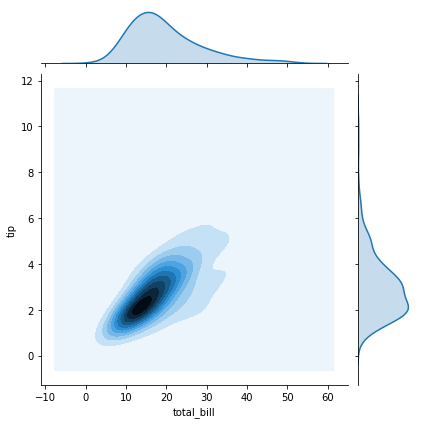
#核密度图
sns.jointplot(x="total_bill", y="tip", data=tips, kind='kde')
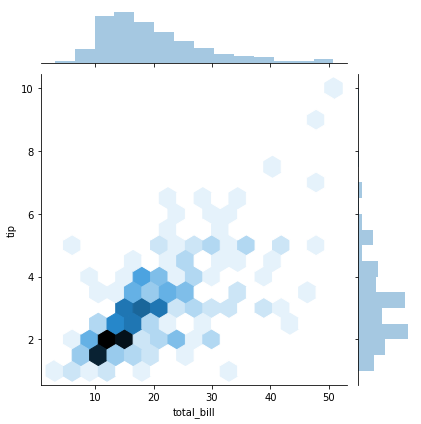
#Hexbin图
sns.jointplot(x="total_bill", y="tip", data=tips, kind='hex')
plt.show()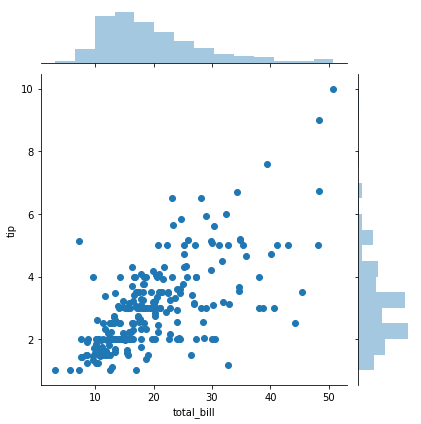
十一、面积图
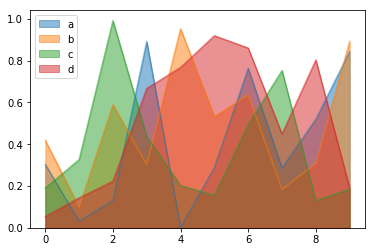
面积图又称区域图,强调数量随时间而变化的程度,也可用于引起人们对总值趋势的注意。
堆积面积图还可以显示部分与整体的关系。折线图和面积图都可以用来帮助我们对趋势进行分析,当数据集有合计关系或者你想要展示局部与整体关系的时候,使用面积图为更好的选择。
df = pd.DataFrame(
np.random.rand(10, 4),
columns=['a', 'b', 'c', 'd'])# 堆面积图
df.plot.area()# 面积图
df.plot.area(stacked=False)

十二、六边形图
六边形图将空间中的点聚合成六边形,然后根据六边形内部的值为这些六边形上色。
df = pd.DataFrame(
np.random.randn(1000, 2),
columns=['a', 'b'])
df['b'] = df['b'] + np.arange(1000)# 关键字参数gridsize;它控制x方向上的六边形数量,默认为100,较大的gridsize意味着更多,更小的bin
df.plot.hexbin(x='a', y='b', gridsize=25)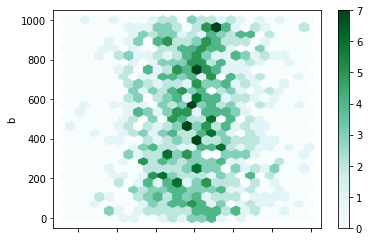
这篇关于python数据分析常用图大集合的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





