本文主要是介绍王小草【机器学习】笔记--支持向量机SVM，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
标签（空格分隔）： 王小草机器学习笔记
1.SVM的原理与目标
1.1 分割超平面
来看上图，假设C和D是两个不想交的凸集，则存在一个超平面P，这个P可以将C和D分离。
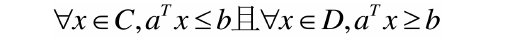
这两个集合的距离，定义为两个集合间元素的最短距离。
做集合C和集合D最短线段的垂直平分线。这条垂直平分线就是分割超平面。
在两个集合之间，可以有无数条分割超平面，使其将两个集合分离，但是如何定义与找出两个集合的“最优”分割超平面呢？
可以这样做：
找到集合“边界”上的若干点，以这些点为基础计算超平面的方向，以两个集合 边界上的这些点的平均作为超平面的“截距”
因为超平面是通过这些点（向量）来支撑形成的，所以我们叫这些吃撑了超平面产生的向量叫做支持向量,support vector.
那么如果两个集合有部分相交，如何定义超平面，从而使得两个集合尽量分开呢？
如下图，在两个集合之间可以画出无数条超平面，到底哪条是最好的，到底哪些是支持向量呢？
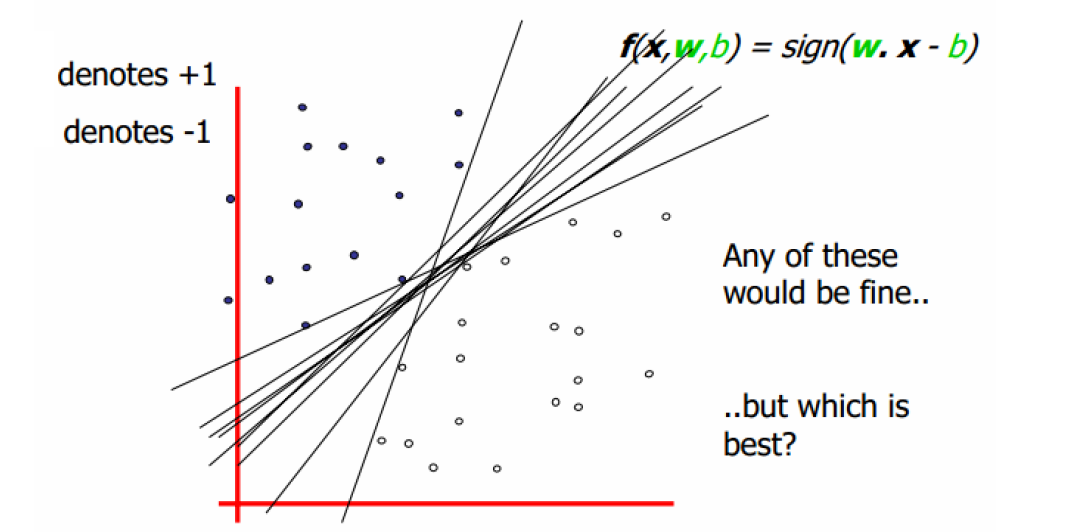
1.2 定义输入数据
假设给定一个特征空间上的训练集为：
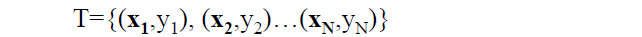
其中，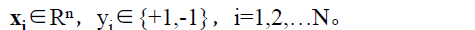
xi为第i个实例（样本），若n>1,则xi为向量。
yi为xi的标记：
当yi=1时，xi为正例
当yi=-1时，xi为负例
（至于为什么正负用（-1，1）表示呢？这个问题也许从来没有想过。其实这里没有太多原理，就是一个标记，你也可以用正2，负-3来标记。只是为了方便，yi/yj=yi*yj的过程中刚好可以相等，便于之后的计算。）
（xi,yi)称为样本点。
1.3 线性可分支持向量机
给定了上面提出的线性可分训练数据集，通过间隔最大化得到分离超平面为
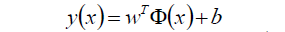
相应的分类决策函数为：
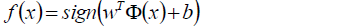
以上决策函数就称为线性可分支持向量机。
这里解释一下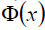
这个东东。
这是某个确定的特征空间转换函数，它的作用是将x映射到更高的维度。
比如我们看到的特征有2个：x1,x2,组成最见到的线性函数可以是w1x1,w2x2.但也许这两个特征并不能很好地描述数据，于是我们进行维度的转化，变成了w1x1+w2x2+w3x1x2+w4x1^2+w5x2^2.于是我们多了三个特征。而这个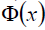
就是笼统地描述x的映射的。
最简单直接的就是：
以上就是线性可分支持向量机的模型表达式。我们要去求出这样一个模型，或者说这样一个超平面y(x),它能够最优地分离两个集合。
其实也就是我们要去一组参数（w,b),使其构建的超平面函数能够最优地分离两个集合。
如下就是一个最优超平面：
又比如说这样：
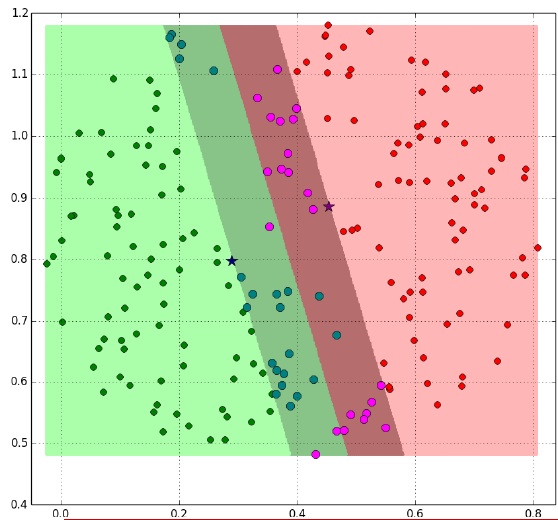
阴影部分是一个“过渡带”，“过渡带”的边界是集合中离超平面最近的样本点落在的地方。
2.SVM的计算过程与算法步骤
2.1 推导目标函数
我们知道了支持向量机是个什么东东了。现在我们要去寻找这个支持向量机，也就是寻找一个最优的超平面。
于是我们要建立一个目标函数。那么如何建立呢？
再来看一下我们的超平面表达式：
有：
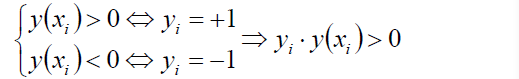
如果这个点落在超平面的上方，那么y就大于0，为正例，反之则为负例。无论正例还是负例，yi * y(xi)总是会大于0.
如果w,b等比缩放，则t*y的值同样缩放，所以有：
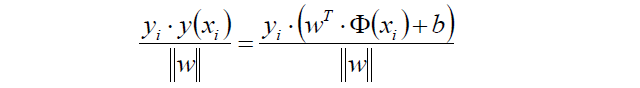
通过上式可以得到目标函数：
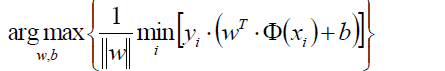
首先是把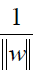
这个东东提出来在外面。
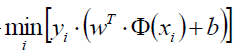表示对某一个（w,b）的参数组合（也就是对某一个超平面）遍历所有的样本点xi，求该样本点到超平面的距离，然后取一个最小的距离。
最外层的max(w,b)表示在所有的（w,b)的组合中（也就是在所有的超平面中），选出那个拥有最大的最短距离的超平面。这个超平面就是我们要寻找的最优超平面。
2.2 转换目标函数
我们有了目标函数了，但创建目标函数的故事还没有完。为了计算的方便，目标函数还要进一步地化简化简，直到处女座们会心一笑为止。
再来看一下我们的分割平面：
|y|总是>=0的。
然而我们总可以通过等比例地缩放w的方法，使得两类点的函数值都满足|y| >= 1。
如果|y| >= 1这个条件满足，那么我们的原目标函数：
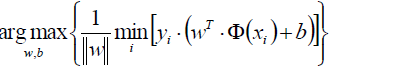
就可以瘦身成新的目标函数：
这个新的目标函数有个约束条件，就是：
来来来，教科书里标准的写法：
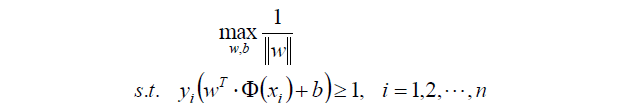
上面求最大值可以转换成求最小值的函数：
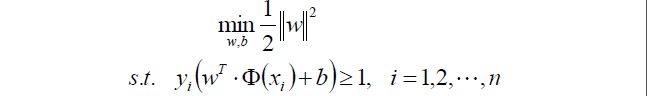
||w||其实就是开根号的（w1^2+w2^2…wn^2),
所以||w||^2就刚好把里面的根号去掉了。
乘以一个1/2是我了等等求导的方便。
2.3 目标函数的求解
终于把目标函数给建立起来了。那么下一步自然是去求目标函数的最优值喽~
因为目标函数带有一个约束条件，所以我们可以用拉格朗日乘子法求解。
啥是拉格朗日乘子法呢？这边小小回顾一下。
如果函数f(x)= 2x+1,约束条件是x+1>0,
那么目标函数可以转换为：
f(x) = 2x+1 - α(x+1)
于是我们的目标函数就转换为了：
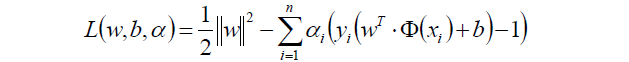
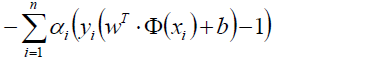中将约束条件-1，所以这一部分的值肯定满足>=0了。
走到这一步，这个目标函数还是不能开始求解，现在我们的问题是极小极大值问题：
我们要将其转换为对偶问题，变成极大极小值问题：
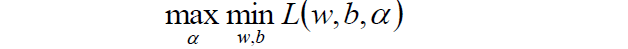
如何获取对偶函数？
首先我们对原目标函数的w和b分别求导：
原目标函数：
对w求导：
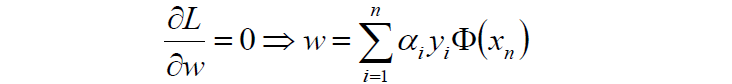
对b求导：
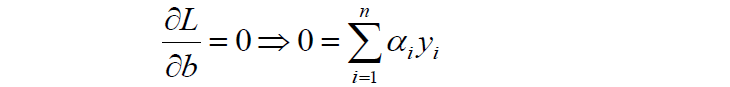
然后将以上w和b的求导函数重新代入原目标函数的w和b中，得到的就是原函数的对偶函数：
这个对偶函数其实求的是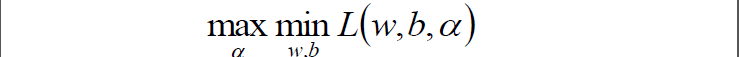
中的minL(w,b)部分（因为对w,b求了偏导）。
于是现在要求的是这个函数的极大值max(a),写成公式就是：
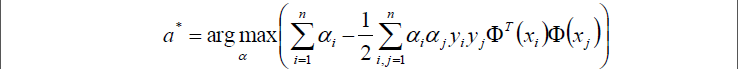
好了，现在我们只需要对上式求出极大值a*，然后将a*代入w求偏导的那个公式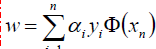
从而求出w.
将w代入超平面的表达式，并且将所有样本点都代入，再除以2，就可以得到b了。
现在的w,b就是我们要寻找的最优超平面的参数。
我们用数学表达式来说明上面的过程：
1.首先是求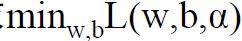
的极大值。即：
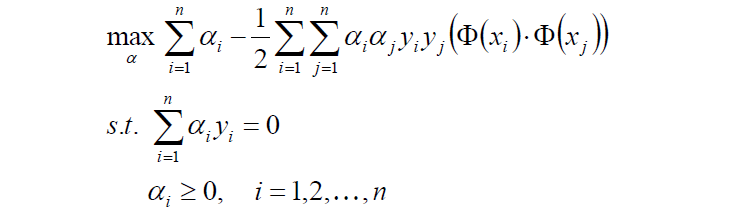
注意有两个约束条件。
2.对目标函数添加符号，转换成求极小值：
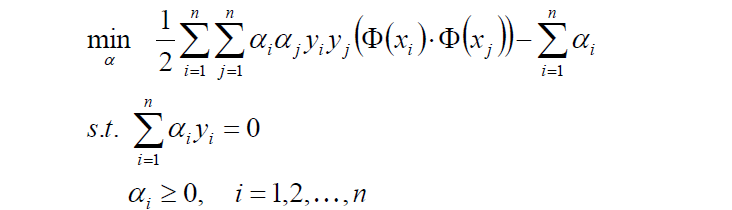
3.计算上面式子的极值求出a*
4.将a*代入，计算w,b
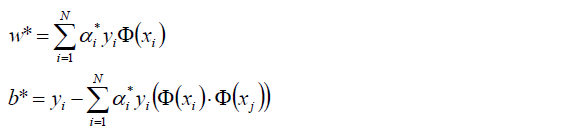
5.求得超平面：
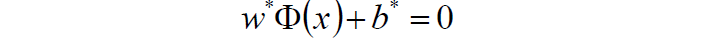
6.求得分类决策函数：
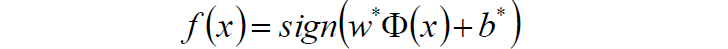
2.4 例子
给定3个数据点：正例点x1=(3,3),x2=(4,3),负x3=(1,1),求线性可分支持向量机。
三个点画出来：
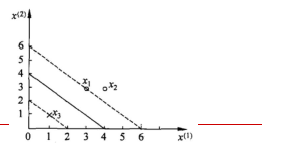
1.首先确定目标函数
2.求得目标函数的极值
3.将求得的极值代入从而求得最优参数w,b
a1=a3=1/4对应的点x1,x3就是支持向量机
代入公式：
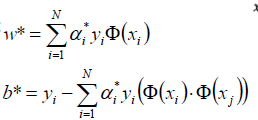
得到w1=w2=0.5, b=-2
4.因此得到分离超平面为
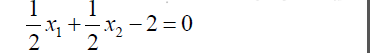
5.得到分离决策函数为：
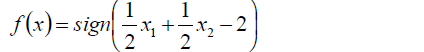
3.线性支持向量机–软间隔最大化
上文第一节与第二节将的都是线性可分支持向量机，也就是说肯定可以找出一个超平面来完全得分割两个集合。
那么是不是分类完全正确的超平面就是最好的呢？
像下图这样的例子，黑色实线完全地将两个集合分开了，但是很明显，我们仍然感觉虚线更好，虽然如果将虚线作为分割面有一个样本被分错了，但是它具有更好的泛化能力。如果画出过渡带的话，实现的过渡带会非常窄，而虚线的过渡带则比较宽。
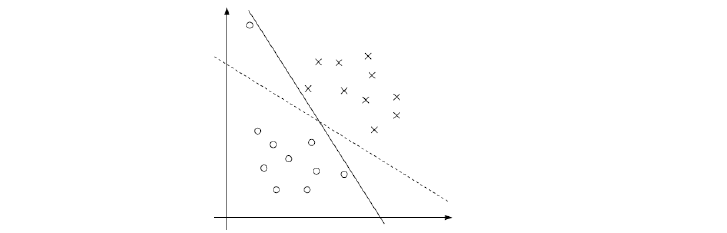
完美地分割面并不是最优的，而且往往还会导致过拟合。我们的样本数据中可能存在的异常值或噪声往往也会导致完美的分割并不完美。对它们的忽视也许会有利于找到更好的分离超平面。
另外，在实际应用中，样本数据往往是线性不可分的，我们根本找不到一个超平面去完全隔离两组数据。
3.1 目标函数及其计算
若数据线性不可分，则增加松弛因子ξi>=0.
使函数间隔加上松弛变量大于等于1.
如此的话约束条件就变成了：
目标函数就变成了：
这个系数C细究一下，如果C为正无穷，那么ξ必须等于0才能使整个公式求得最小值。如果ξ为0的话，就是没有松弛因子，求出来的就是线性可分支持向量机的最优超平面。随着ξ越来越小，超平面会慢慢地趋于泛化，下面这个图中的实现会慢慢变成虚线。
同样对目标函数进行拉格朗日函数的转换：
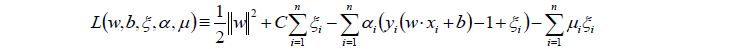
然后对w,b,ξ分别求偏导：
将以上三个求偏导的式子代入L中，得到：
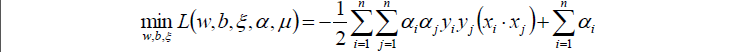
对上式再求极大值：
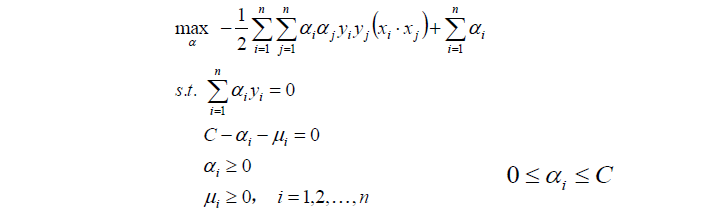
其实，我们发现，目标函数与线性可分支持向量机是一样的，不一样的是约束条件。
上面的约束条件可以经过变化，最终得到对偶问题：
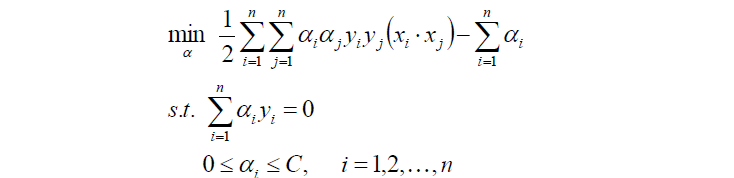
然后对以上式子求最优值a*
将a*代入并计算w,b
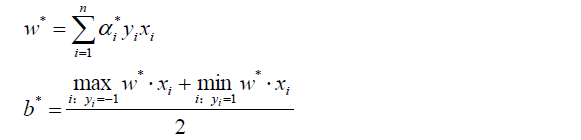
注意，计算b*时，需要使用满足条件0 < aj
3.2 损失函数
如下图，分别有三类损失函数
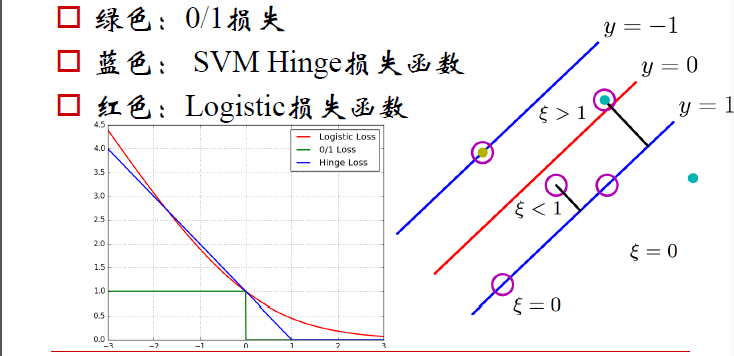
绿色：0/1损失
当负例的点落在y=0这个超平面的下边，说明是分类正确，无论距离超平面所远多近，误差都是0.
当这个负例的样本点落在y=0的上方的时候，说明分类错误，无论距离多远多近，误差都为1.
蓝色：SVM Hinge损失函数
当一个负例的点落在y=1的直线上，距离超平面长度1，，那么1-ξ=1，ξ=0；
当它落在距离超平面0.5的地方，1-ξ=0.5，ξ0.5，也就是说误差为0.5；
当它落在Y=0上的时候，距离为0，1-ξ=0，ξ=1，误差为1；
当这个点落在了y=0的上方，被误分到了正例中，距离算出来应该是负的，比如-0.5，那么1-ξ=-0.5，ξ=-1.5.误差为1.5.
以此类推，画在二维坐标上就是上图中蓝色那根线了。
红色：LOGISTIC损失函数
损失函数的公式为：ln(1+e^-yi)
当yi=0时，损失等于ln2,这样真丑，所以我们给这个损失函数除以ln2.
这样到yi=0时，损失为1，即损失函数过（0，1）点
及时图中的红色线。
4.核函数
SVM+核函数具有极大威力。核函数并不是SVM特有的，核函数可以和其他算法也进行结合，只是核函数与SVM结合的优势非常大。
4.1 什么是核函数
核函数，是将原始输入空间映射到新的特征空间，从而，使得原本线性不可分的样本可能在核空间可分。
之前我们讲的Φ(xi)是第i个样本的特征，Φ(xj)是第j个样本的特征。现在我们将两个样本做一个点乘，并且用k(xi,xj)表示：
k(xi,xj) = Φ(xi) * Φ(xj)
这个k(xi,xj)我们就定义核函数。它是类似于相似度的一个东东。
i可以取值为1->n，j也可以取值为1->n,通过核函数的转换就变成了n*n的一个矩阵:
| j/i | 1 | 2 | … | n |
|---|---|---|---|---|
| 1 | k11 | k12 | … | k1n |
| 2 | … | … | … | k2n |
| … | … | … | … | … |
| n | kn1 | kn2 | … | … |
注意xi和xj是两个样本，如果是特征的维度只有1，那么x就是一个值，如果维度大于等于2，那么x就是一个特征向量。但是k(xi,xj)永远都是一个值。
核函数有很多很多种类，比如：
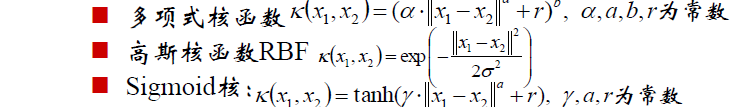
在实际中选择何种核函数呢？
选择核函数，往往依赖先验领域知识，或者通过交叉验证等方法来选择有效的核函数。
如果没有更多的先验信息，则选择使用高斯核函数。
4.2 核函数的映射
我们以高斯核函数为例。
假设任意两个点x1,x2.
||x1-x2||表示x1-x2的模也就是x1与x2的直线距离d。
||x1-x2||^2就是两点距离d的平方。
将d^2再除以2sigma平方，然后前面加个负号
于是从高斯核函数的公式中可以看出，如果距离d越大，则两个点的相似性越小，而k(x1,x2)也越小，反之亦然。所以我们说核函数就是类似于相似性的一个描述。
既然是相似性，那距离为0的核函数k就=1，距离越远的话，k就越小。
对样本点x1,我们可以把所有样本点都和x1求一个k值，那么必然是以x1为中心点，向外一层层画圆，每个圆环上的点都与x1的k值相同，越外的圆k值就越小。就好像一组等高线。正例的在上方形成一个山峰，负例的在下方形成一个山谷。那么对每个样本点都这样做一次。于是画在三维图上就是如下样子：
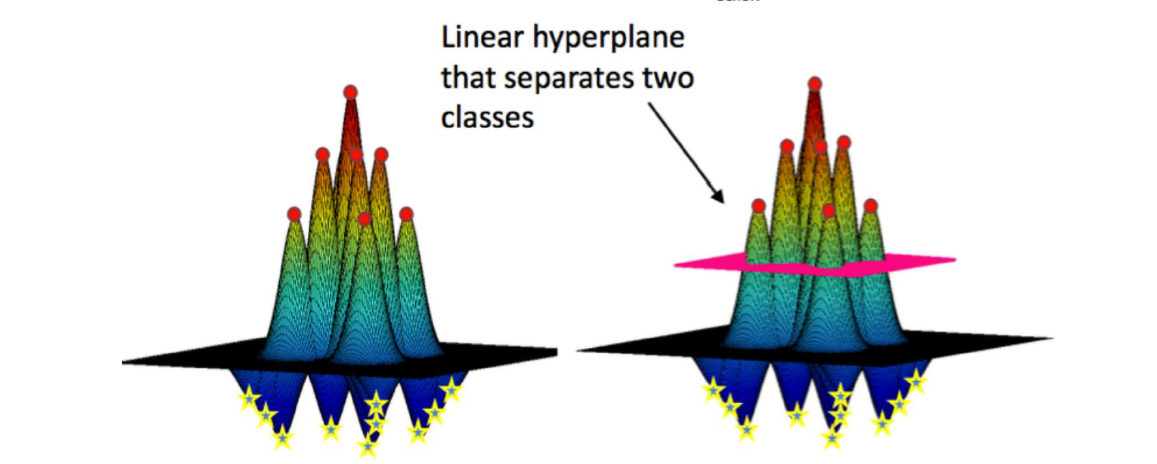
所有的山峰会组成一个大山峰，所有的山谷也会组成一个大山谷，所以，就形成了右下图的样子。
可以看到上图中有一个平面可以将这一整个山切开，上面是正例点，下面是负例点。加这个平面转换到二维左边的样本点图中就是一条分割红蓝点的曲线（分割超平面）。
也就是说，我们将低维的样本点映射到高维，在高维中找到一个最优的分割超平面，然后再将超平面转换到低维中的一条曲线。
那么如何在高维中寻找一个最优分割超平面呢？这个就又回到了我们上面讲的SVM支持向量机的寻找分割超平面的问题了。
所以说核函数与SVM真的是搭配得天衣无缝。
4.3 高斯核
高斯核是什么样的，上面已经讲了。高斯核还有一个特性–就是“高斯核是无穷维的”。
下面这个公式是可以证明得到的，这里不讲如何证明：
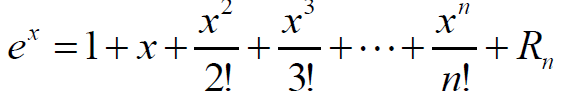
将上面这个公式代入高斯核函数中：
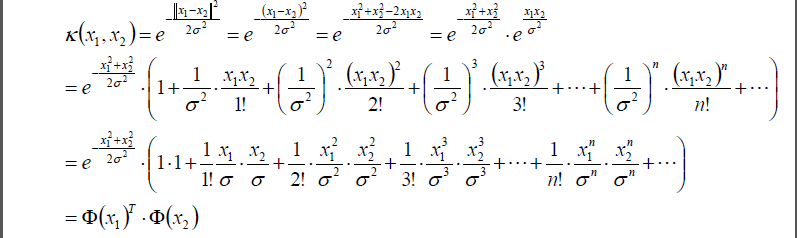
其中，
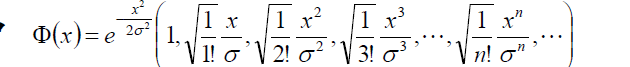
无穷维的高斯核，也就说可以将低维空间的样本构造成如何维度，可以构造任何一种存在的可能。所以，对于一组训练样本，高斯核函数总能有一种方式可以实现对训练样本的100%的拟合。（虽然100%的拟合并不是我们想要的，因为那样会导致过拟合）
5.SMO算法
SMO：Sequential Minimal Optimization序列最小最优化
回顾之前的目标函数求解，函数中有多个拉格朗日乘子a11，a2,..an。
现在对其中两个乘子做优化，其他因子认为是常数。这样就将N个解的问题转换成了两个变量的求解问题，并且目标函数是凸的。求解完之后，将这两个因子剔除掉，然后继续选另外两个来做优化，以此类推。
下面是求解过程（直接截取邹博老师的PPT）
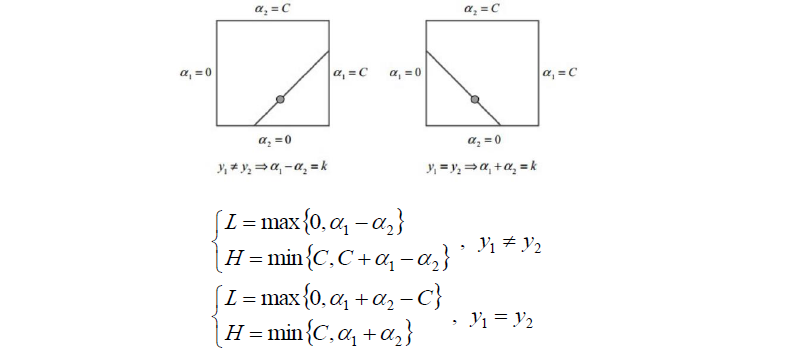
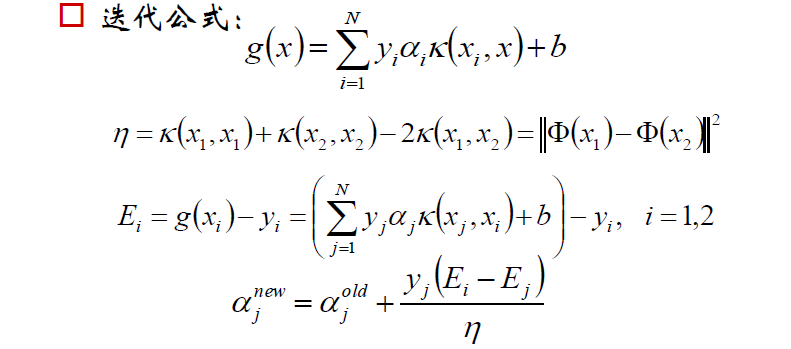
支持向量机的理论就此结束，之后的补充与扩展会直接追加。
这篇关于王小草【机器学习】笔记--支持向量机SVM的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
