本文主要是介绍王小草【机器学习】笔记--分类算法之朴素贝叶斯，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
标签（空格分隔）： 王小草机器学习笔记
##1. 概率论知识
###1.1 先验概率与后验概率
假设有两个事件A和B：
P(A) 为A的先验概率，它不考虑任何B事件的因素；
P(B) 也为B的先验概率，它不考虑任何A事件的影响；
P(A/B) 是B事件发生后，A事件发生的概率，此时A受到B的影响，故称为A的后验概率；
P(B/A) 是A事件发生后，B事件发生的概率，同理，称为B的后验概率。
###1.2 条件概率
要想求得p(A/B),即B发生的情况下A发生的概率，可以运用以下条件概率公式：
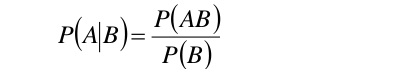
###1.3 全概率公式
假设一个事件A发生的概率由一系列的因素决定：V1，V2，V3…
则事件A的概率可以用下面的全概率公式得到：
P(A) = P(A/V1)P(V1) + P(A/V2)P(V2) + P(A/V3)P(V3)…
表示成公式为：
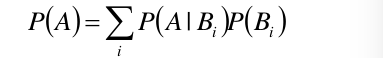
###1.4 贝叶斯定理
根据以上公式，故贝叶斯定理给出：
这个贝叶斯公式的意义在于，在实际的项目中，P(A/B)往往很容易求得，而反之，P(B/A)却很难计算，而实际上，我们往往需要得到的是P(B/A)。因此，贝叶斯定理为此搭起了桥梁。
##2. 朴素贝叶斯分类算法
2.1 基本方法
假设我们有一组训练数据集T：
T = {(x1,y1),(x2,y2),…,(xN,yN)}
x是一个特征向量，长度维n，即每个样本都有n个特征组成。每个特征都会有各自的取值集合，比如a(il)表示第i个特征的第l个值。
y表示的是样本的类别标签，类别集合记为{c1,c2,…,ck}
朴素贝叶斯是通过训练数据集学习联合概率分布P(X,Y)。
根据条件概率公式p(A/B)=P(AB)/P(B)可得p(AB)=P(A/B)P(B)。
所以，要求的联合概率分布p(X,Y)，首先要求得先验概率P(Y),和条件概率p(X/Y).
先验概率P(Y),和条件概率p(X/Y)这两者都是可以通过训练集直接求得的。
先验概率分布：
即计算处训练集中每一个类别（k=1,2…K）出现的概率。
条件概率分布：
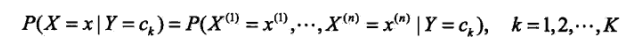
即计算处当类别分别为k=1,2…K时，某租特征出现的概率。
朴素贝叶斯法对条件概率做了“条件独立性假设”，即在知道了Y=ck的分布后，任何特征之间都是独立的。既然是独立的那么它们共同出现的概率就是它们各自出现的概率的乘积。于是，上面的条件概率分布公式可以转换为：
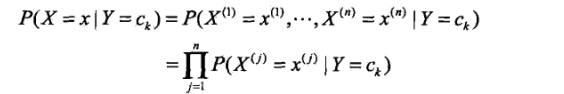
j表示第j个特征。
好了，现在我们知道了如何求先验概率，如何求条件概率，于是我们就可以根据朴素贝叶斯定理去计算后验概率P(Y=ck/X=x)。即去计算当特征为xxx的时候出现Y=ck的概率是多少，最后选取概率最大的那个类别y，作为最终的预测结果。
根据贝叶斯公式，后验概率为：
根据朴素贝叶斯的条件独立假设，后验概率的公式可以改成：
以上是朴素贝叶斯的基本公式。在分类问题中，我们最终要选出概率最大的那个类别，所以朴素贝叶斯分类器可以表示成：
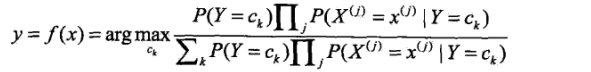
值得注意的是，在以上分类器中的分母对于然后类别ck都是相同的，所以可以将分母去掉，只保留下分子：
恩，好了，要得到以上这个贝叶斯分类器，很显然，需要先根据训练数据去求得先验概率，和条件概率。那么怎么求呢？请看接下去的两节内容，分别介绍了用极大似然估计法估计参数和贝叶斯估计法估计参数。
###2.2 极大似然估计参数
先验概率的极大似然估计：
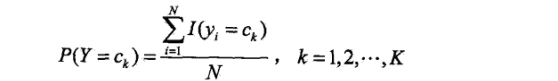
上面这个看上去略显复杂的公式其实就是分别求P(Y=1),P(y=2)…P(Y=K)的出现的概率。也就是求训练集中Y为k类的总数除以总样本数的商。
将每个类别出现的概率都求出来。于是就估计出来所有的先验概率。
条件概率的极大似然估计：
设第j个特征可能取值的集合w为{aj1, aj2,…,ajl},条件概率最大似然估计为：
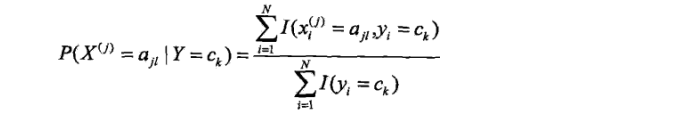
真是公式不可貌相，这个公式的意思非常简单，就是去求在某个类别中出现某个特征的概率。不就是在该类别中该特征出现的次数除以该类别样本的总数吗～
把每个类别出现每个特征的概率都一一求一遍。于是就估计出了所有的条件概率
上面的两个参数都估计好了之后，对于给定的新的实例：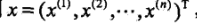
，可以通过后验概率的求得这样的特征会归属于每个各个类别的概率：
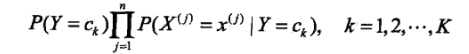
然后选出概率最大的那个类作为这个实例的预测类：
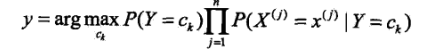
###2.3 贝叶斯估计参数
用极大似然估计法可能会出现所要估计的概率值为0的情况，会影响到后验概率的计算，使得分类产生偏差，于是有了“贝叶斯估计法”。那么它是怎么估计条件概率和先验概率的呢？请看：
条件概率的贝叶斯估计：
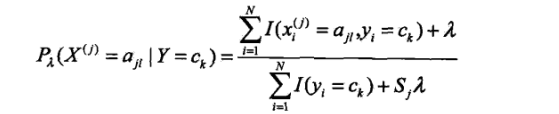
λ>0
也就是说在随机变量的各个取值上加上了一个整数λ。
当λ=0的时候，就等价于最大似然估计。
当λ=1的时候，就称为拉普拉斯平滑Laplace smoothing.
显然对于任何l=1,2,3…l,k=1,2,3…K,都有：
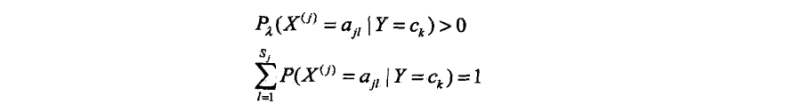
先验概率的贝叶斯估计：
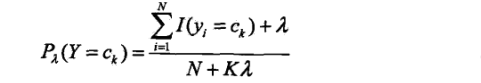
##3. 一元特征案例
例1：假设某公司想要将已有的客户定位成忠实客户和非忠实客户，但是数据有限，只知道每个客户的性别，想要通过性别这个特征去预测今后的新客户成为忠实客户的概率。现在企业已有忠实客户400人，非忠实客户200人；在忠实客户中，有100人性别为男，300人性别为女，在非忠实客户中，有150人为男，50人为女。现在有一个新用户注册了，注册信息填写的性别为男，公司想知道这个客户将成为忠实用户的概率。
为了方便展示，将各事件用字母代替：
A1表示是忠实客户
A2表示是非忠实客户
M表示该客户为男性
F表示该客户为女性
###2.1 类别与特征的说明
在这个案例中，类别变量应该是忠实客户与非忠实客户，这也是我们之后对新用户需要预测的变量；特征就是用于预测类别的因素，特征是已知的，特征取不同的值将影响分类的结果。
###2.2 求解步骤
####第一步：求类别的先验概率
文中已知事件A1和A2的个数，就可以求他们各自的先验概率
P(A1) = 400/600 = 2/3 = 0.67
P(A2) = 200/600 = 1/3 = 0.33
####第二步：求条件概率
我们也已经知道当某个类别出现的后，出现各个特征值的数量
当A1发生后，M为100
P(M/A1) = 100/400 = 1/4 = 0.25
当A1发生后，F为300
P(F/A1) = 300/400 = 3/4 = 0.75
当A2发生后，M为150
P(M/A2) = 150/200 = 3/4 = 0.75
当A2发生后，F为50
P(F/A2) = 50/200 = 1/4 = 0.25
####第三步：求特征的全概率
即为当A1发生时M的概率加上A2发生时M的概率，这样就把所有因素发生时M发生的概率全部遍历了一遍，然后求和
P(M) = P(M/A1)P(A1) + P(M/A2)P(A2) = 0.250.67+0.750.33 = 0.415
同理，以下为F发生的概率和
P(F) = P(F/A1)P(A1) + P(F/A2)P(A2) = 0.750.67+0.250.67 = 0.585
####第四步：根据贝叶斯定理的公式，求类别的后验概率
已知性别为男性，该人为忠实客户的概率
P(A1/M) = P(M/A1)P(A1)/P(M) = 0.25 * 0.67 / 0.415 = 0.4036
已知性别为男，该人为非忠实客户的概率
P(A2/M) = P(M/A2)P(A2)/P(M) = 0.75 * 0.33 / 0.415 = 0.5964
也可以直接用贝叶斯分类器：
y = arg max (P(M/A1)P(A1), P(M/A2)P(A2))
= (0.1675, 0.2475)
= 0.2475 ==> A2非忠实用户！
以上公式中的P(M/A1),P(A1),P(M)三者在上面步骤1，2，3中都已经求得，分别为类别的先验概率，特征的后验概率，特征的全概率。将它们带入贝叶斯定理中，就能快速求得我们需要的概率：当已知性别特征为男，他将成为忠实客户的概率为0.4036，成为非忠实客户的概率为0.5964，显然，非忠实客户的类别得到的概率更高，我们选择概率高的类别，贝叶斯算法认为该新客户应归于“非忠实客户”的类别。
这样，一个只有一个特征的贝叶斯算法就完成了
##4. 多元特征小案例
例2：光靠性别来分类客户显然并不那么精准，通过对访问ip的分析，该公司收集到了这600个客户的所在城市，并将他们分成三类：一线城市，二线城市，三线城市。且已知忠实用户中有250是一线城市，100人是二线城市，50人是三线城市；非忠实用户中有40人是一线城市，60人是二线城市，100人是三线城市。
若那个新用户除了知道他是男性外，也知道了他来自一线城市上海，现在重新计算这个新用户成为忠实客户的概率。
为了方便展示，将各事件用字母代替：
A1表示是忠实客户
A2表示是非忠实客户
M表示该客户为男性
F表示该客户为女性
C1 表示一线城市
C2 表示二线城市
C3 表示三线城市
###4.1 类别，特征与假设的说明
在这个案例中，类别变量仍然是忠实客户与非忠实客户；特征变量有2个：性别，城市。
当涉及两个及以上的特征时，我们假设特征之间是相互独立，不会互相影响的。如果A和B两个事件独立，那么A和B共同发生的概率是各自先验概率相乘
P(AB) = P(A)P(B)
###4.2 求解步骤
####第一步：求类别的先验概率
文中已知事件A1和A2的个数，就可以求他们各自的先验概率
P(A1) = 400/600 = 2/3 = 0.67
P(A2) = 200/600 = 1/3 = 0.33
####步骤二：求每个特征的条件概率
案例中有2个类别，2个特征，第一个特征有2个取值，第二个特征有3个取值，条件概率共有10组.
P(M/A1) = 100/400 = 1/4
P(M/A2) = 150/200 = 3/4
P(F/A1) = 300/400 = 3/4
P(F/A2) = 50/200 = 1/4
P(C1/A1) = 250/400 = 5/8
P(C1/A2) = 40/200 = 1/5
P(C2/A1) = 100/400 = 1/4
P(C2/A2) = 60/200 = 3/10
P(C3/A1) = 50/400 = 1/8
P(C3/A2) = 100/200 =1/2
####步骤三：求后验概率
根据条件独立假设，新的实例特征维男性与一线城市，根据贝叶斯分类器，后延概率为：
P(A1/M,C1) = P(A1)P(M/A1)P(C1/A1) = 0.670.250.625 = 0.1046
P(A2/M,C1) = P(A2)P(M/A2)P(C1/A2) = 0.330.750.2 = 0.0495
由结果课件，当出现特征（男性，一线城市）的用户更有可能称为忠实用户。
以上两个案例使用的是最大似然估计，也可以使用贝叶斯估计参数的方法来做，效果可能会更好。
##5. 贝叶斯分类模型实战，代码演示
这里列举一个小小的案例，调用spark的mmllib包来实现朴素贝叶斯算法。以下是案例的背景介绍，scala代码s
###5.1 实例一
####5.5.1 研究目的：分辨出微博上的粉丝是不是僵尸粉
####5.5.2 数据预处理：
(1) 设置应变量：标记类别
将真实用户标记为1，虚假用户（僵尸粉）标记为0
(2) 设置自变量：特征向量
选取3个因子作为特征，并将其转换为数值形式
v1=发微博数目/注册天数
v2=好友数目/注册天数
v3=是否使用手机，使用手机为1，不适用手机为-1
其中v1,v2是连续型变量，我们将其人为地转变成类别变量（当然连续型的变量贝叶斯也可以实现）
v1<0.05 时 v1=-1
0.75>v1>=0.05 时v1=0
v1>=0.75 时 v1=1
v2<0.05 时 v2=-1
0.75>v2>=0.05 时v2=0
v2>=0.75 时 v2=1
故标签与3个因子的向量可以表述为：
v：（1,0） ——类别
v1：（-1,0,1） ——特征1
v2：（-1,0,1） ——特征2
v3：（1，-1） ——特征3
(3) 数据格式
将数据格式调整为（label,factor1 factor2 …. factorn）的格式，如此便可以用MLUtils.loadLabeledPiont读取并将其判断成为LabledPoint格式进行处理。
最终整理的数据如下：
0,1.0 1.0 0
1,-2.0 -1.0 1
1,-1.0 -2.0 1
1,-2.0 -1.0 1
0,0.0 0.0 1
1,-2.0 -2.0 0
0,1.0 0.0 0
1,-2.0 -2.0 0
1,-1.0 -2.0 1
1,-1.0 -1.0 1
0,1.0 0.0 0
0,0.0 0.0 1
####5.5.3 求解模型
import org.apache.spark.mllib.{SparkConf,SparkContext}
import org.apache.spark.mllib.classification.NaiveBayes
import org.apache.spark.mllib.linalg.Vector
import org.apache.spark.mllib.regression.LabeledPointobject BayesTest {def main(args:Aarray[String]){//创建spark实例val conf =new SparkConf().setAppName("BayesTest").setMaster("local")val sc = new SparkContext(conf)//导入数据val file = MLUtils.loadLabeledPoint(sc,"//")//处理数据:转换数据格式为Doubleval data = file.map{ line = >val parts = line.split(,) LabeldPoint(parts(0).toDouble,Vectors.dense(parts(1).split(' ').map(_.toDouble)))//随机分组数据为trainning and test两类val splits = data.randomSplit(Array(0.7,0.3)，seed=11L)val train = splits(0) //设置训练数据集val test = splits(1) //设置测试数据集//根据训练数据集训练模型val BayesModel = NaiveBayes.train(train,lamda=1.0)//模型的评估//用test数据验证模型,变成（预测的label,实际的label)格式val prediction = test.map(p=>(model.predict(p.feature),p.labeel)) //计算准确度:预测类别准确的个数val accuracy = 1.0*prediction.filter(label = label._1 == label._2).count()println(accurancy)
}
}
这篇关于王小草【机器学习】笔记--分类算法之朴素贝叶斯的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
