做点记录：Attention稀疏化与线性化

本文主要是介绍做点记录：Attention稀疏化与线性化，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

背景

本文来自苏剑林老师的为节约而生：从标准Attention到稀疏Attention。
Attention 来源于 18 年初的 Attention is All You Need（乘性 Attention）, 其核心在于 QKV 三个向量序列的交互融合，其中，QK 的交互给出了两两向量之间的某种权重，最后由 V 按照权重求和得到输出序列。常见的 Attention 为：$$Attention(\mathbf{Q},\mathbf{K},\mathbf{V})=softmax\left(\frac{\mathbf{Q}{\mathbf{K}}^{\top }}{\sqrt{d_k}}\right)\mathbf{V}$$
此外，还有加性 Attention，但该类 Attention 并行不容易实现或实现所需资源较多，所以一般只用来将变长向量序列编码为固定长度的向量（取代简单的 Pooling）。
乘性 Attention 中，最广泛使用的是 Self-Attention，该情况下，QKV 均为同一个 X 经过线性变换得到的。这样，输出结果就是跟 X 一样长的向量序列，并且能够直接捕捉 X 中任意两个向量的关联，而且易于并行。 这都是 Self Attention 的优点。
理论上来讲，Self-Attention 的计算时间和显存占用均为平方级别，因此不可避免地会导致 OOM 。

Softmax 妙用

常见的 Attention 的一般化定义：$$Attention(\mathbf{Q},\mathbf{K},\mathbf{V}{)}_i=\frac{{\sum }_{j=1}^n\sin ({\mathbf{q}}_i,{\mathbf{k}}_j){\mathbf{v}}_j}{{\sum }_{j=1}^n\sin ({\mathbf{q}}_i,{\mathbf{k}}_j)}$$
为保证 Attention 的相似特性，要确保 $sim(q_i,k_j)\ge 0$ 恒成立。这种形式的 Attention 在 CV 中也被称为 Non-Local 网络。若直接去除 Softmax，$sim(q_i,k_j)=q_i^T{k}_j$，无法保证内积的非负性，因此有几个可行的方案：

核函数

一个自然的想法是，若 $q_i,k_j$ 的每个元素均为非负，那么内积自然也就是非负。为完成该点，给 $q_i,k_j$ 各自加激活函数，即：$\sin ({\mathbf{q}}_i,{\mathbf{k}}_j)=\varphi ({\mathbf{q}}_i{)}^{\top }\phi ({\mathbf{k}}_j)$，其中，$\varphi (\cdot ),\phi (\cdot )$ 均为值域非负的激活函数。该公式可联想到和方法，特别是当 $\varphi =\phi$ 时，$\varphi$ 相当于核函数，而 $<\varphi (q_i),\phi (k_j)>$ 就是通过核函数定义的内积。

妙用 SoftMax

若 Q 在 d 维是归一化的，K 在 n 维是归一化的，那么 $Q{K}^T$ 就自动归一化，即：$Attention(\mathbf{Q},\mathbf{K},\mathbf{V})=softma{x}_1(\mathbf{Q})softma{x}_2(\mathbf{K}{)}^{\top }\mathbf{V}$, 各自给 QK 加 softmax，而不是 $Q{K}^T$ 计算完才加 Softmax。

作者自己的构思

该构思的出发点来自对 Attention 的原始定义，由泰勒展开可知：$e^{{\mathbf{q}}_i^{\top }{\mathbf{k}}_j}\approx 1+{\mathbf{q}}_i^{\top }{\mathbf{k}}_j$，若 ${\mathbf{q}}_i^{\top }{\mathbf{k}}_j\ge -1$，那么可保证右端的非负性，从而可以让 $sim(q_i,k_j)=1+q_i^T{k}_j$。因此，想要保证 ${\mathbf{q}}_i^{\top }{\mathbf{k}}_j\ge -1$，只需要分别对 $q_i,k_j$ 做 $l_2$ 归一化。所以，最终方案为: $\sin ({\mathbf{q}}_i,{\mathbf{k}}_j)=1+{\left(\frac{{\mathbf{q}}_i}{\Vert {\mathbf{q}}_i\Vert }\right)}^{\top }\left(\frac{{\mathbf{k}}_j}{\Vert {\mathbf{k}}_j\Vert }\right)$

Sparse Attention

所谓自注意力是 $O(n^2)$ 的，因为它要对序列中任意两向量都要计算相关度，得到 $n^2$ 大小的相关度矩阵：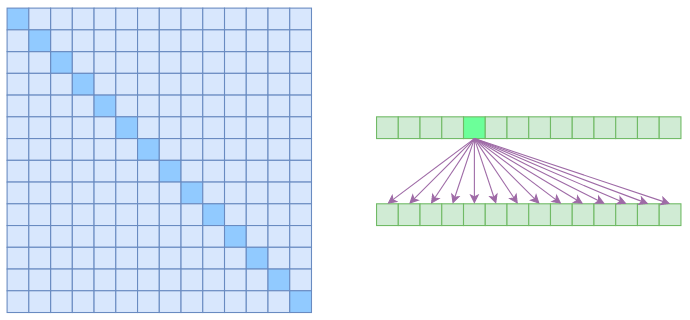
上图中，左边显示了注意力矩阵，右边显示其关联性，这表明每个元素都与序列内所有元素关联。若要节省显存，加快计算速度，那么基本的思路就是减少关联性计算，也就是认为每个元素只与序列内一部分元素有关，此即稀疏 Attention的基本原理。文章所介绍的 Sparse Attention，来源于 OpenAI 的论文 Generating Long Sequences with Sparse Transformers

Atrous Self Attention

首先，引入Atrous Self Attention, 中文名为膨胀自注意力、空洞自注意力等。该注意力启发自膨胀卷积，如下图所示，其对相关性进行约束，强行要求每个元素只与其相对距离为 k, 2k, 3k 的元素关联，其中，k>1 是预先设定的超参数。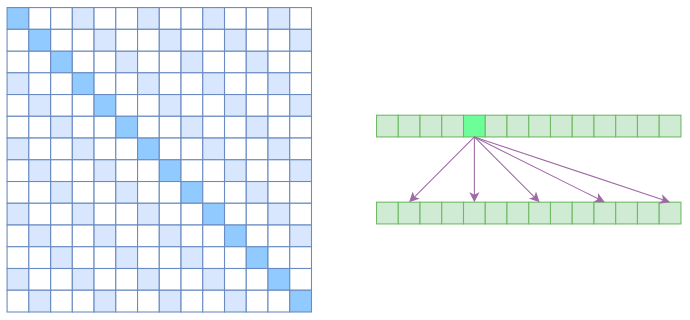
在这种计算方式中，每个元素只与 $\frac{N}{k}$ 个元素计算相关性，因此，理想情况下，运算效率和显存占用都变为 $O(\frac{N^2}{k})$

Local Self Attention

另一个要引入的过渡概念是 Local Self Attention，中文可称之为“局部自注意力”。其实自注意力机制在 CV 领域统称为“Non Local”，而显然 Local Self Attention 则要放弃全局关联，重新引入局部关联。具体来说也很简单，就是约束每个元素只与前后 k 个元素以及自身有关联，如下图所示：

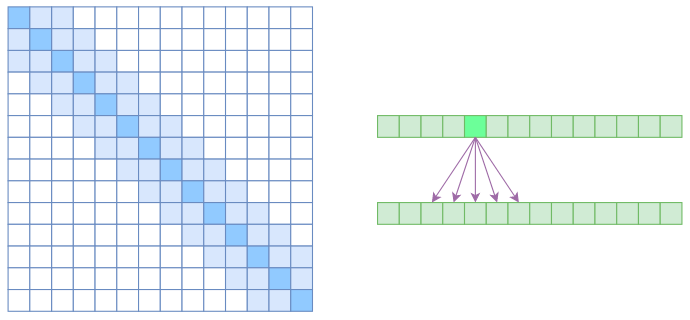
也即，相对距离超过 k 的权重值均设定为 0。对于 Local Self Attention 来说，每个元素只跟 2k+1 个元素算相关性，这样一来理想情况下运行效率和显存占用都变成了 $O((2k+1)n)\sim O(kn)$ 了，也就是说随着 n 而线性增长，这是一个很理想的性质——当然也直接牺牲了长程关联性。

Sparse Self-Attention

到此，就可以很自然地引入 OpenAI 的 Sparse Self Attention 了。我们留意到， Atrous Self Attention 是带有一些洞的，而 Local Self Attention 正好填补了这些洞，所以一个简单的方式就是将 Local Self Attention 和 Atrous Self Attention 交替使用，两者累积起来，理论上也可以学习到全局关联性，也省了显存。
简单来说，假定两层 Attention，第一层采用 Local Self Attention，第二层采用 Atrous Self Attention。那么，在第一层，输出的每个向量均融合局部的几个输入向量，第二层的输出理论上可与任意输入向量相关，实现长程关联。
但是 OpenAI 是将两个 Atrous Self Attention 和 Local Self Attention 合并为一个，如下图所示：

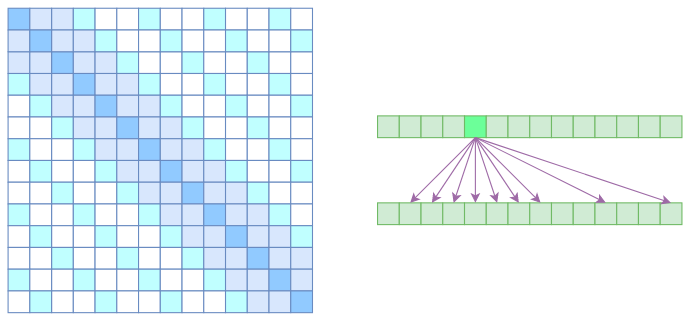
从注意力矩阵上看就很容易理解了，就是除了相对距离不超过 k 的、相对距离为 k, 2k, 3k,… 的注意力都设为 0，这样一来 Attention 就具有**“局部紧密相关和远程稀疏相关”**的特性，这对很多任务来说可能是一个不错的先验，因为真正需要密集的长程关联的任务事实上是很少的。

与之后的 LongFormer 类似，该方法有两个不足之处：

1. 保留的注意力区域由人工决定，带有很大的主观性；
2. 需要从编程上进行特定优化，才能得到一个高效的实现，不容易推广。

Reformer

该工作将 Attention 的复杂度降至 $O(nlongn)$。某种意义上来说，也算稀疏 Attention 的一种，只不过其稀疏模式由 LSH（Locality Sensitive Hashing） 技术（近似地）快速地找到最大的若干个 Attention 值，然后只计算那若干个值。
此外，Reformer 通过构造可逆形式的 FFN（Feedforward Network）替换掉原来的 FFN，然后重新设计反向传播过程，从而降低了显存占用量。
所以，相比前述稀疏 Attention，Reformer 解决了它的第一个缺点，但是依然有第二个缺点：实现起来复杂度高。要实现 LSH 形式的 Attention 比标准的 Attention 复杂多了，对可逆网络重写反向传播过程对普通读者来说更是遥不可及。

LinFormer

该模型依然保留原始 Scale-Dot Attention 形式，但在进行 Attention 之前，用两个 $m\times n$ 的矩阵 $E,F$ 分别对 $K,V$ 投影，即变为 $Attention(\mathbf{Q},\mathbf{K},\mathbf{V})=softmax(\mathbf{Q}(\mathbf{EK}{)}^{\top })\mathbf{FV}$。这样，$Q(EK{)}^T$ 就只是一个 $n\times m$ 的矩阵，而作者声称对于哪怕很大的序列，$n,m$ 也可保持一个适当的常数，从而该 Attention 就是线性的。
但是，原论文中对于长序列作者只做了 MLM 任务，而很明显 MLM 并不那么需要长程依赖，所以这个实验没什么说服力。因此，Linformer 是不是真的 Linear，还有待商榷。

下采样技术

从结果上看，LinFormer 的 $Q(EK{)}^T$ 就是将序列变短（下采样），实现该操作的最朴素的办法是 Pooling，所以也可尝试采用 Pooling。当然，其实还有其他的下采样技术，比如可以通过 stride > 1 的一维卷积来实现，基于这个思路，或许我们可以把 FFN 里边的 Position-Wise 全连接换成 stride > 1 的一维卷积？总之这方面应该也能玩出很多花样来，不过跟 Linformer 一样，这样糅合之后做自回归生成就很难了。

采用随机投影将 Attention 的复杂度线性化

针对平方复杂度的 Attention，改进思路有两种：稀疏化和线性化。本部分介绍一个新的改进工作 Performer，其目标是通过随机投影，在不损失精度的情况下，将 Attention 的复杂度线性化。理想情况下我们可以不用重新训练模型，输出结果也不会有明显变化，但是复杂度降到了 $O(n)$。其最大贡献在于，找到一个很好的映射方案：$$\begin{array}{rl}{e}^{q\cdot k}& ={\mathbb{E}}_{\mathbf{\omega }\sim \mathcal{N}(\mathbf{\omega };0,1_d)}\left[e^{\mathbf{\omega }\cdot \mathbf{q}-\Vert \mathbf{q}{\Vert }^2/2}\times e^{\mathbf{\omega }\cdot \mathbf{k}-\Vert \mathbf{k}{\Vert }^2/2}\right]\\ & \approx \underset{\mathbf{q}}{\underbrace{\frac{1}{\sqrt{m}}\left(\begin{array}{c}{e}^{{\mathbf{\omega }}_1\cdot \mathbf{q}-\Vert \mathbf{q}{\Vert }^2/2}\\ e^{{\mathbf{\omega }}_2\cdot \mathbf{q}-\Vert \mathbf{q}{\Vert }^2/2}\\ ⋮\\ e^{{\mathbf{\omega }}_m\cdot \mathbf{q}-\Vert \mathbf{q}{\Vert }^2/2}\end{array}\right)}}\cdot \underset{\mathbf{k}}{\underbrace{\frac{1}{\sqrt{m}}\left(\begin{array}{c}{e}^{{\mathbf{\omega }}_1\cdot \mathbf{k}-\Vert \mathbf{k}{\Vert }^2/2}\\ e^{{\mathbf{\omega }}_2\cdot \mathbf{k}-\Vert \mathbf{k}{\Vert }^2/2}\\ ⋮\\ e^{{\mathbf{\omega }}_m\cdot \mathbf{k}-\Vert \mathbf{k}{\Vert }^2/2}\end{array}\right)}}\end{array}$$ 第一个等号意味着只要从标准正态分布中采样无穷尽的 $\omega$，然后算出 $e^{\mathbf{\omega }\cdot \mathbf{q}-\Vert \mathbf{q}{\Vert }^2/2}\times e^{\mathbf{\omega }\cdot \mathbf{k}-\Vert \mathbf{k}{\Vert }^2/2}$ 的平均，结果就等于 $e^{q\cdot k}$，写成积分形式就是：$$\begin{array}{rl}& \frac{1}{(2\pi {)}^{d/2}}\int e^{-\Vert \mathbf{\omega }{\Vert }^2/2}\times e^{\mathbf{\omega }\cdot \mathbf{q}-\Vert \mathbf{q}{\Vert }^2/2}\times e^{\mathbf{\omega }\cdot \mathbf{k}-\Vert \mathbf{k}{\Vert }^2/2}d\mathbf{\omega }\\ & =\frac{1}{(2\pi {)}^{d/2}}\int e^{-\Vert \mathbf{\omega }-\mathbf{q}-\mathbf{k}{\Vert }^2/2+\mathbf{q}\cdot \mathbf{k}}d\mathbf{\omega }\\ & =e^{q\cdot \mathbf{k}}\end{array}$$
当然，实际情况中只能采样有限的 m 个，因此就得到约等，正好可表示为两个 m 维向量的内积的形式，此即 $e^{q\cdot k}\approx \tilde{q}\cdot \tilde{k}$。借助该加你，就可以得到两个 d 维向量的内积的直属，转为两个 m 维向量的内积，理论上，就可以将 head_size=d 的标准 Attention，转化为 head_size=m 的线性 Attention。
文中，各个 $\omega$ 是独立重复地从 $\mathcal{N}(\omega ;0,1_d)$ 中采样得到，若将这些 $\omega$ 正交化（保持模长不变，仅对其方向进行施密特正交化），能有效降低估算的方差，提高单次估算的平均精度。该策略有效的最根本原因是采样分布 $\mathcal{N}(\omega ;0,1_d)$ 的各向同性，即其概率密度函数 $(2\pi {)}^{-d/2}{e}^{-\Vert \mathbf{\omega }{\Vert }^2/2}$ 值依赖于 $\omega$ 的模长 $\Vert \omega \Vert$，所以在方向上是均匀的。若要降低估算的方差，那么就要降低采样的随机性，使得采样的结果更为均匀。而各个向量正交化，是方向上均匀的一种实现方式，换句话说，将各个 ${\omega }_i$ 正交化促进了采样结果的均匀化，从而降低估算的方差。此外，正交化操作一般只对 $m\le d$ 有效，若 $m>d$，则将每 d 个向量为一组分别进行正交化。可以联想到，正交化操作只是让采样的方向更均匀，若做得彻底些，可以让采样的模长也均匀化。具体来说，将标准正态分布变换为 d 维球坐标得到其概率微元：$$\frac{1}{(2\pi {)}^{d/2}}{r}^{d-1}{e}^{-r^2/2}drdS$$ 其中，$dS={\sin }^{d-2}{\phi }_1{\sin }^{d-3}{\phi }_2\cdots \sin {\phi }_{d-2}d{\phi }_{1}d{\phi }_2\cdots d{\phi }_{d-1}$ 代表在 d 维球面上的积分微元。上式就显示出，标准正态分布是均匀的，模长的概率密度函数正比于 $r^{d-1}{e}^{-r^2/2}$, 我们可以定义其累积概率函数：$$P_d(r\le R)=\frac{{\int }_0^R{r}^{d-1}{e}^{-r^2/2}dr}{{\int }_0^{\infty }{r}^{d-1}{e}^{-r^2/2}dr}$$ 若要采样 m 个样本，那么让 $P_d(r\le R_i)=\frac{i}{m+1},i=1,2,\cdots ,m$，从中解出 m 个 $R_i$ 作为模长即可。

这篇关于做点记录：Attention稀疏化与线性化的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---