本文主要是介绍东北大学离散数学,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!










第一章 命题逻辑
第一节 命题及命题的真值
第二节 逻辑连结词
第三节 命题逻辑中的命题符号化
第四节 命题公式及其真值表
第五节 命题公式的等价
第六节 重言式与重言蕴含式
第七节 析取范式与合取范式
第八节 主析取范式








第二篇 集合论
第一节 基本概念与集合的表示方法
第二节 集合间的关系
第三节 特殊集合
第四节 集合的运算





![]()







![]()



![]()





第五节 包含排斥定理





![]()







第三章 集合论初步
第四章 二元关系

第一节 序偶与集合的笛卡尔积












第二节 关系及其表示方法







、
第三节 关系的性质










第四节 关系的复合运算









第五节 关系的求逆运算





第六节 关系的闭包运算



第五章 函数
第一节 函数的基本概念










第二节 函数的复合








第三节 函数的求逆运算


![]()


![]()
第四节 集合的等式

















第六章 组合数学初步

第一节 加法原理与乘法原理








第二节 排列与组合


![]()













第三节 二项式定理与组合恒等式





第四节 多项式定理




第七章 代数系统
第一节 二元运算及其性质













第二节 二元运算中的特殊元




















第三节 代数系统的同态与同构


![]()



![]()





![]()



第四节 代数系统同构的性质














第五节 半群和独异点






第六节 群的定义及性质










![]()








第七节 子群及其证明







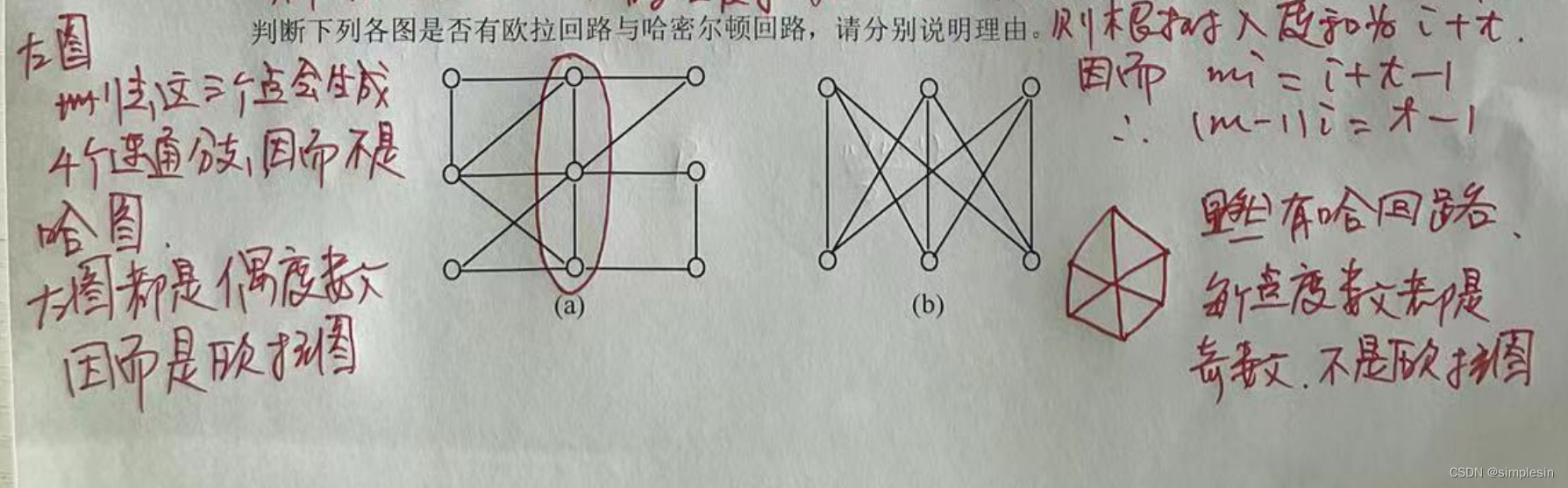
这篇关于东北大学离散数学的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!