本文主要是介绍论文笔记|A Practical Guide to Training Restricted Boltzmann Machines,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1 简介 1
2 RBMs和对比散度的概览 1
3 当使用对比散度时如何收集统计信息 2
3.1 更新隐藏状态 2
3.2 更新可见状态 3
4 Mini-batch大小 3
5 监控学习的过程 3
6 监控过拟合 3
7 学习率 3
8 初始化权重和偏置 4
9 Momentum 4
10 权重衰减 4
11 鼓励稀疏的隐藏活跃 4
12 隐藏单元的数量 4
13 单元的不同类型 5
14 contrastive divergence变体 5
15 显示在学习中发生了什么 5
16 使用RBM进行识别任务 5
17 处理缺失值 5
4 The size of a mini-batch
【理想的mini-batch 大小经常等于分类的数量,每一个mini-batch应该包含每个类别的一个样例,减少采样错误。】
在单个训练案例上估计梯度后更新权重是可能的,但将训练集划分为10 ~ 100个案例的小"小批量"往往更有效率。这使得矩阵-矩阵乘法可以被使用,这在GPU板上或在Matlab中都是非常有利的。
为了避免在改变小批量的大小时不得不改变学习率,将在小批量上计算的总梯度除以小批量的大小是很有帮助的,因此在谈论学习率时,我们将假设它们乘以在小批量上计算的平均每例梯度,而不是小批量的总梯度。
在使用随机梯度下降法时,使小批量样本过大是一个严重的错误。增加小批量的N倍导致更可靠的梯度估计,但不会增加最大稳定学习率的N倍,因此净效应(net effect)是每个梯度评估的权重更新较小。
4.1 A recipe for dividing the training set into mini-batches 将训练集划分为小批量的方法
(1)理想的mini-batch 大小经常等于分类的数量,每一个mini-batch应该包含每个类别的一个样例,减少采样错误。
对于包含少量等概率类(equiprobable classes)的数据集,理想的mini - batch大小往往等于类的数量,并且每个mini - batch应该包含每个类的一个样本,以减少从单个mini - batch估计整个训练集的梯度时的抽样误差。
(2)对于其他数据集,首先将训练样本的顺序随机化,然后使用大小约为10的mini-batch。
5 Monitoring the progress of learning 监控学习进度
【容易计算训练数据和重建之间的平方误差,这个衡量指标通常在训练过程中输出。
它系统性的战胜了下面两个指标,第一个是在训练数据的空间分布和RBM均衡分布的差异;第二个是交替吉布斯马尔可夫链的mixing rate。】
在学习过程中经常要输出数据与重建结果之间的误差平方和。在整个训练集上的重建误差应该在学习开始时迅速持续下降,然后缓慢地下降。
由于梯度估计中存在噪声,在初始快速下降后,个体小批量上的重建误差会平缓波动。当使用高动量时,它还可能以几个小批量的周期平缓振荡。
虽然方便,但重建误差实际上是一个很差的衡量标准。CDn学习不是一个近似最优的函数,特别是当n > > 1时,它混淆了在学习过程中不断变化的两个不同的量。
①首先是训练数据的经验分布与RBM的均衡分布之间的差异。
②第二个是交替Gibbs Markov链的混合率(mixing rate)。如果混合率很低,即使在数据和模型的分布有很大差异的情况下,重构误差也会很小。随着权重的增加,混合率下降,因此重建误差的减小并不一定意味着模型在改善,反之,小幅度的增加并不一定意味着模型在恶化。然而,大的增加是一个不好的征兆,除非它们是暂时的,并且是由学习率、动量、权重成本或稀疏性元参数的变化引起的。
5.1 A recipe for using the reconstruction error 重建误差的使用方法
用它但不要相信它。如果你想知道在学习过程中发生了什么,可以使用多个直方图和图形,如第15节所述。还可以使用退火重要采样Annealed Importance Sampling对持有数据进行密度估计。如果学习有标签数据(见第16节)的联合密度模型,要考虑监测训练数据和保留的验证集上的判别性能。
6 Monitoring the overfitting
在学习一个生成模型时,需要监控的明显量(the obvious quantity)是当前模型分配给一个数据点的概率。当这种概率开始降低时,对于被保留的验证数据是而停止学习的时候。对于大型的RBM来说,计算这个概率是非常困难的,因为它需要知道配分函数。尽管如此,通过比较训练数据和留出的验证数据的自由能(free energies),可以直接监测过拟合。在这种比较中,配分函数抵消掉了。一个数据向量的自由能可以在一个与隐藏单元数(见第16.1节)成线性关系的时间内计算。如果模型完全不过拟合,则训练和验证数据上的平均自由能应该大致相同。随着模型开始过拟合,验证数据的平均自由能相对于训练数据的平均自由能会上升,这个差距代表过拟合的量。
6.1 A recipe for monitoring the overfitting 监测过拟合的方法
每隔若干个epochs后,计算训练数据代表子集的平均自由能,并将其与验证集的平均自由能进行比较。始终使用相同的训练数据子集。如果差距开始增长,模型就会过拟合,尽管训练数据的概率可能会比差距增长得更快,验证数据的概率仍然可能会提高。在计算希望比较的两个平均值时,确保使用相同的权重。
7 The learning rate 学习率
【学习率不能很大。】
如果学习率过大,重建误差通常会急剧增加,权重可能会爆炸。
如果在网络学习的同时降低学习率重构误差通常会显著下降。这未必是好的。这在一定程度上是由于随机权重更新中的噪声水平较小,并且在长期中通常伴随着较慢的学习。然而,在学习结束时,它通常以降低学习速率为代价。
在几个更新之间对权重进行平均是一种替代方法,以去除最终权重中的一些噪声。
7.1 A recipe for setting the learning rates for weights and biases 为权重和偏置设置学习率的方法
设置学习率(马克斯·韦林,个人通讯, 2002)的一个很好的经验法则是查看权重更新的直方图和权重的直方图。更新的权重应该是(到一个数量级左右)的10^−3倍。
当一个单位有一个very large fan-in ,更新应该较小,因为许多相同方向的微小变化可以很容易地逆转梯度的符号。反之,对于偏置,更新可以更大。
8 The initial values of the weights and biases 权重和偏置的初始值
权重通常初始化为从零均值标准差约为0.01高斯中选择的小的随机值。使用较大的随机值可以加快初始学习速度,但可能导致最终模型略差。应该小心确保初始权重值不允许典型的可见向量驱动隐藏单元概率非常接近1或0,因为这显著地减慢了学习。
如果用于学习的统计量是随机的,初始权重都可以为零,因为统计量中的噪声会使隐藏单元变得彼此不同,即使它们具有相同的连通性。
通常将可见单元i的偏置初始化为log [ pi / ( 1-pi ) ],其中pi是unit i所在的训练向量的比例。如果没有做到这一点,学习的早期阶段将使用隐藏单元使i以近似pi的概率开启。
当使用稀疏目标概率t (见第11节)时,将隐藏偏差初始化为log [ t / ( 1-t) ]是有意义的。不然的话,0的初始隐藏偏差通常也是很好的。还可以用大约- 4的较大负偏差去激活隐藏单元作为促进稀疏性的粗略方法。
8.1 A recipe for setting the initial values of the weights and biases 设定权重和偏差初始值的公式
对于从标准差为0.01的零均值高斯中选择的权重,使用较小的随机值。将隐藏偏差设置为0,将可见偏差设置为log [ pi / ( 1-pi) ],其中pi是单位i所在的训练向量的比例。时不时检查一下隐藏单元的活动,保证它们并不是一直开启或关闭的。
9 Momentum
【当目标函数包含长的、狭窄的、相当直的峡谷,同时该峡谷沿着峡谷的地面有一个温和但持续的坡度和沿着峡谷的边上有许多陡峭的坡度,Momentum是一个简单的方法来增加学习的速度。Momentum方法模拟一个重的球在地面滚动。该球沿着峡谷的地面增加速度,但没有跨过峡谷,因为在峡谷的对面边上的相反梯度随着时间推移抵消了彼此。】
当目标函数包含长的、窄的和相当平直的沟壑时,沿着沟壑的底部具有平缓但一致的梯度,而在沟壑的两侧具有更陡的梯度时,动量是一种简单的提高学习速度的方法。
动量法模拟重球沿表面滚动。小球沿着沟谷底部建立速度,但没有穿过沟谷,因为随着时间的推移,沟谷两侧相反的梯度相互抵消。动量方法不使用估计的梯度乘以学习率来增加参数的值,而是使用这个量来增加参数的速度v,然后使用当前的速度作为参数增量。
假设球的速度随时间衰减,而"动量"元参数α是在新的小批量上计算梯度后剩下的先前速度的分数:
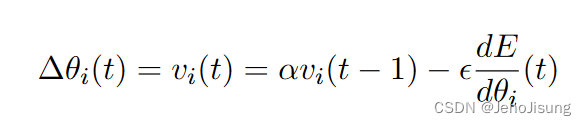
若梯度保持不变,则末端速度将超过![]() 的1 / ( 1-α )倍。动量为0.9的10倍是这个元参数的典型设置。动量法中的时间平滑避免了简单地将学习率提高1 / ( 1-α)而引起的跨越沟壑的发散振荡。
的1 / ( 1-α )倍。动量为0.9的10倍是这个元参数的典型设置。动量法中的时间平滑避免了简单地将学习率提高1 / ( 1-α)而引起的跨越沟壑的发散振荡。
动量方法使参数沿着非最速下降方向移动,因此它与共轭梯度等方法有一些相似之处,但它使用之前的梯度的方式要简单得多。与对每个参数使用不同学习率的方法不同,当沟壑与参数轴不匹配时,动量的作用也是一样的。
观察动量方法( Tijmen Tieleman, 2008)的另一种方式如下:它相当于将学习率提高1 / ( 1-α),但通过将全部增量分成一系列指数衰减的部分来延迟每个梯度估计的全部效果。这使得系统在感受到增量的全部效应之前,通过移动到具有相反梯度的参数空间区域,来响应早期的设置。这反过来又允许学习率更大,而不会引起不稳定的振荡。
在学习开始时,随机的初始参数值可能会产生非常大的梯度,并且系统不太可能处于沟壑的底部,因此通常最好以0.5的低动量开始进行多次参数更新。这种非常保守的动量通常会通过横跨沟壑( Hinton , 1978)的阻尼振荡使学习比没有动量时更稳定。
9 .1 A recipe for using momentum 使用动量的方法
以0.5的动量开始。一旦降低重构误差的初始进度较大,已经稳定在平缓的进度,增加动量至0.9。这种冲击可能会导致重建误差的短暂增加。如果这会导致更持久的不稳定性,继续将学习率降低为原来的一半,直到不稳定性消失。
10 Weight-decay
【权重衰减是在正常的梯度上增加一个额外的项。这个额外的项是一个函数的导数,惩罚大的权重。如最简单的惩罚函数:L2。】
权重衰减是通过在正常梯度中增加一个额外的项来实现的。额外项是惩罚大权重的函数的导数。最简单的惩罚函数,称为" L2 ",是权重的平方和乘以一个系数的一半,这个系数将被称为权重成本。
重要的是将惩罚项的导数乘以学习率。否则,学习率的变化改变的是正在优化的函数,而不是仅仅改变优化过程。
在RBM中使用体重衰减有四种不同的原因。首先是通过减少对训练数据的过拟合来提高对新数据的泛化能力。7 .第二种是通过收缩无用权重,使得隐藏单元的感受野更加平滑,可解释性更强。第三种是"不粘"隐藏单元,这些隐藏单元在训练早期已经发展了非常大的重量,并且要么总是牢牢地开着,要么总是牢牢地关着。让这样的单元重新变得有用的更好方法是使用如第11节所述的"稀疏性"目标。第四个原因是提高了交替Gibbs Markov链的混合速率。在权重较小的情况下,Markov链混合得更快。CD的学习过程是建立在忽略从Markov链( Hinton , Osindero和Teh , 2006)的后面步骤中得到的导数的基础上的,因此,当混合速度较快时,它倾向于更好地近似最大似然学习。被忽略的导数是小的,原因如下:当一个Markov链非常接近它的平稳分布时,从该链中建模样本的最佳参数非常接近它的当前参数。
一种叫做' L1 '的不同形式的权重衰减是使用权重绝对值之和的导数。这往往会导致许多权重恰好为零,而允许少数权重增长相当大。这样可以使权重的解释更加容易。例如,在对图像进行特征学习时,L1权重衰减往往会导致强局部化的感受野。
控制权重大小的另一种方法是对每个单元的传入权重的平方和或绝对值施加一个最大允许值。在每次权重更新后,如果超过这个最大值,则重新调整权重。这有助于避免隐藏单元在极小的权重下陷入困境,但稀疏性目标可能是避免这一问题的更好方法。
10.1 A recipe for using weight-decay
对于RBM,L2权重衰减的权重成本系数的合理取值范围通常为0.01 ~ 0.00001。权重成本通常不应用于隐藏和可见的偏差,因为这些偏差的数量要少得多,因此它们不太可能导致过拟合。此外,偏差有时需要相当大。
尝试初始重量成本为0.0001。如果使用退火重要性抽样(萨拉赫丁诺夫和Murray , 2008)在保留的验证集上进行密度估计,则尝试将权重成本调整为2的因子来优化密度。重量-成本的微小差异不太可能引起性能的巨大差异。如果你正在训练一个联合密度模型,允许你在验证集上测试判别性能,这可以代替密度用于优化权重-成本。然而,无论哪种情况,请记住,权重衰减不仅仅是防止过拟合。这也增加了混合率,使得CD学习更好地逼近最大似然。因此,即使过拟合不是问题,因为训练数据的供应是无限的,权重衰减仍然可以提供帮助。
11 Encouraging sparse hidden activities 稀疏的隐藏活动
【很少活跃的隐藏单元比那些大约一半时间都活跃的隐藏单元是更容易解释的。同时,识别能力可以通过使用那些很少活跃的特征来改善】
只有很少活跃的隐藏单元通常比大约一半时间活跃的隐藏单元更容易解释。此外,有时通过使用只有很少活跃的( Nair和Hinton , 2009)的特征来提高判别性能。
二进制隐藏单元的稀疏活动可以通过指定一个"稀疏目标"来实现,这个"稀疏目标"是活动的期望概率,p < < 1。然后使用一个额外的惩罚项来鼓励活跃的实际概率,q,接近p。q是通过使用一个指数衰减的平均值来估计一个单位在每个小批中活跃的概率:
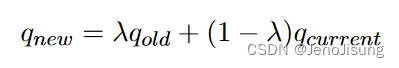
式中:qcurrent为隐藏单元在当前小批量上的平均激活概率。
使用的自然惩罚度量是期望分布和实际分布之间的交叉熵:
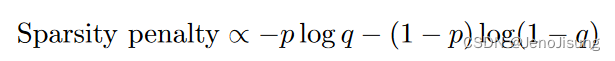
对于logistic units,它对一个单位的总投入有q - p的简单导数。该导数由一个称为"稀疏度-代价"的元参数缩放,用于调整每个隐藏单元的偏置和传入权重。对两者应用相同的导数是很重要的。例如,如果导数只应用于偏差,通常会使偏差变得更负,以确保隐藏的单元很少出现,但权重会变得更正,以使单元更有用。
11.1 A recipe for sparsity
设定稀疏度目标在0.01 ~ 0.19之间。设定q估计值的衰减率λ在0.9 ~ 0.99之间。对隐藏单元的平均活动进行直方图,并设置稀疏度代价,使隐藏单元在目标附近具有平均概率。如果概率紧密地聚集在目标值周围,则降低稀疏代价,使其对学习的主要目标干扰更小。
12 The number of hidden units
【如果每张图片有1000像素,那训练10000张图像,这大约要百万参数级别模型。这就需要1000个全局的连接的隐藏单元。】
从判别性机器学习中得到的直觉对于确定合理的隐藏单元数是一个不好的指导。在判别学习中,一个训练案例对参数施加的约束量等于它指定标签所需的比特数。标签通常包含很少的比特信息,因此使用比训练情况更多的参数通常会导致严重的过拟合。然而,在学习高维数据的生成模型时,指定一个数据向量所需要的比特数决定了每个训练案例对模型的参数施加了多少约束。这可以比指定一个标签所需的比特数大几个数量级。因此,如果每张图像包含1000个像素,那么将100万个参数拟合到10000张训练图像可能是相当合理的。这将允许1000个全局连接的隐藏单元。如果隐藏单元是局部连接的,或者使用权重共享,则可以使用更多的隐藏单元。
12.1 A recipe for choosing the number of hidden units
假设主要问题是过拟合,而不是训练或测试时的计算量,如果使用一个好的模型(即在一个好的模型下,估计一个数据向量的典型负log2概率),估计它需要多少比特来描述每个数据向量。然后将该估计值乘以训练案例的数量,并使用一些大约小一个数量级的参数。如果使用的是一个非常小的稀疏目标,那么可能可以使用更多的隐藏单元。如果训练案例是高度冗余的,因为它们通常会用于非常大的训练集,因此需要使用较少的参数。
13 Different types of unit
【RBM是使用二值的可见和隐藏单元发展起来的,但许多其他类型的单元可以使用。有如下类型:
1)Softmax and multinomial(多项式) units
2)Gaussian visible units
3)Gaussian visible and hidden units
4)Binomial(二项式) units
5)Binomial units】
RBM是利用二进制的可见单元和隐藏单元开发的,但也可以使用许多其他类型的单元。在(韦林等, 2005)中给出了指数族中单位的一般处理方法。其他类型单元的主要用途是处理没有被二进制(或逻辑)可见单元很好地建模的数据。
13.1 Softmax and multinomial units
对于一个二进制单元,开启的概率由其总输入的Logistic sigmoid函数给出,x。
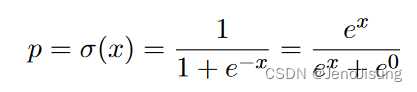
单位贡献的能量在开时为- x,在关时为0。方程15明确指出,每两个可能状态的概率正比于其能量的负指数。这可以推广到K个替代态。
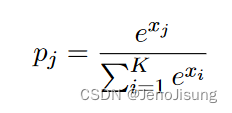
这通常被称为" softmax "单元。它是处理具有K个替代值的不以任何方式排序的数量的合适方法。一个softmax可以看成是一组状态相互约束的二元组,使得K个状态中只有一个取值为1,其余的取值为0。以这种方式来看,softmax中二进制单元的学习规则与标准二进制单元的学习规则相同。唯一不同的是状态概率的计算和样本的采样方式。
softmax单元的进一步推广是从概率分布中采样N次(带替换),而不是仅仅采样一次。这K个不同的状态可以有大于1的整数值,但这些值必须加到N上。这被称为多项式单位,并且学习规则是不变的。
13.2 Gaussian visible units
对于自然图像的分块或用于表示语音的Mel - Cepstrum系数等数据,逻辑单元的代表性很差。一种解决方案是将二进制可见单元替换为具有独立高斯噪声的线性单元。那么能量函数就变成了:
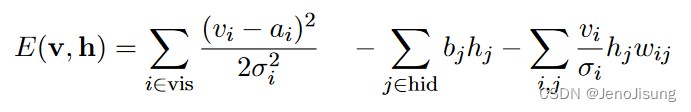
其中σ i是可见单元i的高斯噪声的标准差。
可以学习每个可见单元噪声的方差,但使用CD1是困难的。在许多应用中,首先将数据的每个分量标准化为零均值和单位方差,然后使用无噪声重构,式( 17 )中的方差设置为1,要容易得多。然后,高斯可见单元的重建值等于它从二进制隐藏单元自上而下的输入加上它的偏置。
学习率需要比使用二进制可见单元时小一到两个数量级,文献中报道的一些失败很可能是由于使用了太大的学习率。需要较小的学习率,因为在重建中没有一个分量大小的上界,如果一个分量变得非常大,由它产生的权重将得到一个非常大的学习信号。由于具有二进制的隐藏和可见单元,每个训练情况的学习信号必须介于- 1和1之间,因此二进制-二进制网络更加稳定。
13.3 Gaussian visible and hidden units
如果可见单元和隐藏单元都是高斯的,那么不稳定性问题变得更加严重。个体活动通过二次"包含"项保持在其均值附近,系数由假设噪声水平的标准差决定:
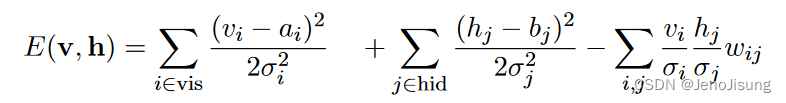
如果权重矩阵的任何一个特征值变得足够大,那么二次交互项可以主导包含项,那么就不存在能量的下界,可以通过在相应的特征向量方向上放大活动来实现。在足够小的学习率下,CD1可以检测并纠正这些方向,因此可以使用所有高斯单元学习无向版本的因子分析模型( Marks and莫韦利安, 2001),但这比使用EM ( Ghahramani和Hinton , 1996)学习有向模型要困难。
13.4 Binomial units 二项式单位
得到一个在0到N范围内含噪整数值的单位的一个简单方法是将一个二进制单位的N个副本分开,并赋予它们所有相同的权重和偏置( Teh和Hinton , 2001)。由于所有副本接受相同的总输入,它们都有相同的开启概率p,且只需计算一次。令期望值为Np,期望值的方差为Np( 1-p)。对于较小的p,这表现为一个泊松单位,但随着p趋近于1,方差又变得很小,这可能是不可取的。此外,对于p的小值,p的增长在总输入中呈指数增长。
这使得学习的稳定性远不如第13.5节所述的校正线性单元。利用权重共享从二元单元中合成新型单元的一个好处是,二元-二元RBM的数学基础保持不变。
13.5 Rectified linear units 校正线性单元
对二项式单元的微小修改使得它们作为真实神经元的模型更有趣,也更有利于实际应用。所有副本仍然具有相同的学习权重向量w和相同的学习偏差b,但每个副本都有一个不同的、固定的偏差偏移量。当偏移量为- 0.5,- 1.5,- 2.5,.. - ( N-0 . 5)时,拷贝概率之和非常接近于一个闭合形式:
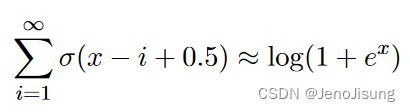
式中:x = vwT + b。因此,所有副本的总活动就像一个修正线性单元的平滑版本,对于足够大的输入饱和。尽管log ( 1 + ex)不属于指数族,但我们可以使用一组具有共享权重和固定偏置的二进制单元对其进行精确建模。
这个集合没有比普通的二进制单元更多的参数,但它提供了一个更具表现力的变量。方差为σ ( x ),因此,被牢牢关闭的单元不会产生噪声,并且当x很大时,噪声不会变大。
给每个副本一个与固定偏移量不同的偏移量的缺点是需要多次使用logistic函数才能得到正确采样一个整数值所需的概率。但是,可以采用一种快速近似方法,即校正后的线性单元的采样值不受限制为整数。取而代之的是max( 0 , x + N ( 0,1 )),其中N ( 0、1 )是具有零均值和单位方差的高斯噪声。在使用CD1 ( Nair和Hinton , 2010)进行训练时,这种类型的校正线性单元似乎对可见单元或隐藏单元都能很好地工作。
如果可见单元和隐藏单元都是线性修正的,则可能需要更小的学习率,以避免活动或权重更新中的不稳定动态。如果两个校正线性单元之间的权重大于1,则两个单元都有很高的活跃度所能达到的能量没有下界,因此没有合适的概率分布。尽管如此,对比散度学习仍然可以工作,只要学习率足够低,以给出检测和纠正方向的学习时间,如果允许运行多次迭代,马尔科夫链将会爆破。由校正线性单元组成的RBM比由高斯单元组成的RBM更稳定,因为校正防止了权重动态的双相振荡,即一个小批量的单位在不同的高正活性之间交替,下一个小批量的单位在非常高的负活性之间交替。
14 Varieties of contrastive divergence
(讲了一个“persistent contrastive divergence”,其比CD1在建立密集模型上更好,但在非密集上不比CD1好。)
虽然CD1不是最大似然学习的一个很好的近似,但是当学习一个RBM时,这似乎并不重要,以便为训练更高层次的RBM提供隐藏的特征。CD1保证了隐藏特征保留了数据向量中的大部分信息,使用更接近最大似然但在保留数据向量中的信息方面更差的CD形式并不一定是一个好的想法。然而,如果目标是学习一个RBM是一个好的密度或联合密度模型,那么CD1是远没有达到最优的。
在学习初期,权重较小,混合速度较快,因此CD1对最大似然提供了很好的逼近。随着权重的增加,混合越来越差,逐渐增加CDn (卡雷拉-佩皮尼昂and Hinton , 2005 ;萨拉赫丁诺夫et al , 2007)中的n是有意义的。当n增加时,用于学习的成对统计量的差异会增加,因此可能需要降低学习率。
与CD1更激进的偏离被称为"持续对比分歧" (蒂勒曼, 2008)。而不是在一个数据向量处初始化每个交替的吉布斯马尔科夫链,这是CD学习的本质,而是跟踪多个持久链或"幻想粒子"的状态。每条持久链的隐状态和可见状态在每次权重更新后都更新一次(或少数)。然后,学习信号是在小批量数据上测量的成对统计量与在持久链上测量的成对统计量之间的差值。通常情况下,持续链的数量与小批量的大小相同,但这并没有很好的理由。持久性链的混合速度惊人,因为权重更新通过提高该状态的能量( Tieleman和Hinton , 2009)将每个链从其当前状态中驱逐。
当使用持续CD时,学习速率通常需要小得多,并且学习的早期阶段在减少重建误差方面要慢得多。在学习的早期阶段,持久性链往往具有非常相关的状态,但这种情况会随着时间的推移而消失。最后的重构误差也通常比CD1大,因为持续的CD是渐近稳定的,进行最大似然学习,而不是试图使一步重建的分布类似于数据的分布。持续CD学习的模型显著优于CD1甚至CD10 (蒂勒曼, 2008),如果以建立数据的最佳密度模型为目的,则是推荐的方法。
持久性CD可以通过在标准参数中添加一个学习非常快但衰减也非常快的"快速权重"的叠加( Tieleman和Hinton , 2009)来改进。这些快速权重改善了持久链的混合。然而,快速权重的使用引入了更多的元参数,在这里将不作进一步讨论。
15 Displaying what is happening during learning
学习出错的方式有很多种,大多数常见问题很容易用正确的图形显示进行诊断。下面介绍的三种类型的显示比简单地监测重建误差更深入地了解正在发生的事情。
权重的直方图、可见偏差和隐藏偏差是非常有用的。此外,在更新这些参数时,检查这些参数增量的直方图是有用的,尽管在每次更新后制作这些直方图是浪费的。
对于可见单元具有空间或时间结构(例如图像或语音)的域,为每个隐藏单元显示连接该隐藏单元与可见单元的权重是非常有用的。这些"接受域"是可视化隐藏单元学习到什么特征的好方法。在显示多个隐藏单元的感受野时,对不同的隐藏单元使用不同的尺度会产生很大的误导。感受野的灰度显示通常不如伪彩色显示那么漂亮,但却比伪彩色显示包含更多的信息。
对于单个小批量数据,非常有用的是看到一个范围为[ 0、1 ]的二维灰度显示,它显示了每个二进制隐藏单元在一个mini - batch10中每个训练情况下的概率。这立刻可以让你看到一些隐藏单元是否从未使用过,或者一些训练案例是否激活了异常大或小数量的隐藏单元。它还显示了隐藏单元是如何确定的。当学习正常工作时,这种显示应该是完全随机的,没有任何明显的垂直或水平线。可以使用直方图来代替这种显示,但它需要相当多的直方图来传达相同的信息。
16 使用RBM进行识别任务
提出了三种方式:
1)使用RBM学到的隐藏特征作为输入;
2)对每个类别训练一个独立的RBM;
3)使用一个单独的RBM训练一个联合密集模型,有两个可见单元集合,除了一个表示数据向量的单元,还有一个“softmax”标签单元表示类别。
17 处理缺失值
如标签数据的缺失。
这篇关于论文笔记|A Practical Guide to Training Restricted Boltzmann Machines的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






