Leetcod面试经典150题刷题记录 —— 矩阵篇

本文主要是介绍Leetcod面试经典150题刷题记录 —— 矩阵篇，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 有效的数独

题目链接：有效的数独 - leetcode
题目描述：
请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）
注意：
一个有效的数独（部分已被填充）不一定是可解的。
只需要根据以上规则，验证已经填入的数字是否有效即可。
空白格用 '.' 表示。
题目归纳：
略

class Solution:def isValidSudoku(self, board: List[List[str]]) -> bool:# (1) board的行数为m，列数为n，m = n = 9# (2) 该求解算法应只遍历board一次# (3) 遍历过程更新hashtable的计数，并判断是否满足有效数独# (4) 0<=i,j<9，故对于(i,j)单元格，该单元格所在的小九宫格，其对应行数为i//3，列数为j//3，均向下取整, 0<=i//3, j//3 <9# (5) 创建二维数组 rows与columns，分别记录每行、每列中，每个数字的出现次数# (6) 创建三维数组 subboxes，记录每个小九宫格中，每个数字的出现次数#     其中rows[i][index]表示数独i行j列单元格所在 行，数字index+1出现的次数#     其中columns[j][index]表示数独i行j列单元格所在 列，数字index+1出现的次数#     其中subboxes[i//3][j//3][index]表示数独i行j列单元格所在 小九宫格，数字index+1出现的次数#     其中 1<= index+1 <= 9# (7) 若board[i][j]非空，其字符串值为数字n，则将#     rows[i][n-1] += 1#     columns[j][n-1] += 1#     subboxes[i//3][j//3][n-1] += 1#     若更新后的计数 >1，则不符合有效数独条件，返回false#     若更新后的计数 <=1，则符合有效数独条件，返回truerows = [[0] * 9 for _ in range(9)] columns = [[0] * 9 for _ in range(9)]subboxes = [[[0] * 9 for _ in range(3)] for _ in range(3)]for i in range(9):for j in range(9):ch = board[i][j]if ch != '.': # 数字digit = int(ch) - 1rows[i][digit] += 1columns[j][digit] += 1subboxes[int(i/3)][int(j/3)][digit] += 1if rows[i][digit] > 1 or                       columns[j][digit] > 1 or                       subboxes[int(i/3)][int(j/3)][digit] > 1:return Falsereturn True

这里有一个巨坑，我不踩不知道，一踩吓一跳。就是在生成rows，columns，subboxes时，我一开始采用的方式是：

rows = [ [0]*9 ]*9
columns = [ [0]*9 ]*9
subboxes = [[[0] * 9 for _ in range(3)] for _ in range(3)]

但是这样有个问题，问大模型，大模型给的回答是，[[0]*9]*9是通过重复一个已存在的子列表来创建一个新的列表，这个新列表中有 9 个相同的子列表，每个子列表都有 9 个元素，每个元素值都是 0。这意味着这个新列表中的每个子列表都是同一个对象，修改其中一个子列表会影响其他子列表。注意这句，会影响其他子列表，所以，为稳妥起见并养成良好习惯，生成列表还是用列表推导式，而不要用这种快速写法。

2. 螺旋矩阵

题目链接：螺旋矩阵 - leetcode
题目描述：
给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

题目归纳：
略

解题思路：
(1) 解法： 旋转图像 - leetcode官方题解

Python

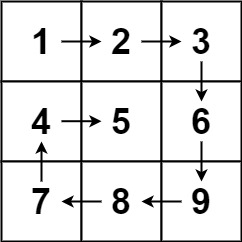
class Solution:def spiralOrder(self, matrix: List[List[int]]) -> List[int]:# 洋葱式模拟法# (1)将矩阵看成若干层，输出次序：最外层->次外层->最内层# [[1, 1, 1, 1, 1, 1, 1],# [1, 2, 2, 2, 2, 2, 1],# [1, 2, 3, 3, 3, 2, 1],# [1, 2, 2, 2, 2, 2, 1],# [1, 1, 1, 1, 1, 1, 1]]# (2)对于每层，顺序又是顺时针的# (top, left) -> (top, right)#      ^              |#      |              v# (bottom, left) <- (bottom, right)#if not matrix or not matrix[0]:return list()rows, columns = len(matrix), len(matrix[0])ans = list()left, right, top, bottom = 0, columns-1, 0, rows-1while left <= right and top <= bottom: # 3*3方阵最后会出现left=right, top=bottomfor column in range(left, right+1): # [left,right]，从左到右ans.append(matrix[top][column])for row in range(top+1, bottom+1): # [top+1, bottom]，从上到下ans.append(matrix[row][right]) if left < right and top < bottom: # 左右未交汇，上下未交汇for column in range(right-1, left, -1): # right-1, ... , left+1，从右到左ans.append(matrix[bottom][column])for row in range(bottom, top, -1): # bottom, ..., top+1，从下到上ans.append(matrix[row][left])left += 1right -= 1top += 1bottom -= 1return ans

3. 旋转图像

题目链接：螺旋矩阵 - leetcode
题目描述：
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
题目归纳：
略

解题思路：
(1) 解法： 旋转图像 - leetcode官方题解

Python

额外开辟数组空间

class Solution:def rotate(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""# (1)关键性质# 矩阵中的第 i 行第 j 个元素# 旋转后会出现在# 倒数第 i 列第 j 个位置，即第 j 行倒数第i列，即# matrix[row][col] -> matrix[col][(n-1) -row]n = len(matrix) # 长宽相等matrix_new = [ [0 for j in range(n)] for i in range(n)]# 开始旋转for i in range(n):for j in range(n):matrix_new[j][(n-1)-i] = matrix[i][j]# 不能写成引用赋值：matrix = matrix_newmatrix[::] = matrix_new

原地置换法

class Solution:def rotate(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""# 解法二，原地置换法，不使用额外矩阵# 将矩阵按行分块，有#  a_0#  a_1#  ...#  a_n-1# (1)将矩阵按行对称轴进行上下反转#  a_n-1#  a_n-2#  ...#  a_0# (2)T转置。这就是最终答案，顺时针旋转90°# a_n-1_T, ..., a_1_T, a_0_T。# #      |     |#  --- · --- · --- : row1#      |     |#  --- · --- · --- : row2#      |     |#    col1   col2# 可以发现，顺时针旋转90°，即# row1 --> col2# row2 --> col1# col1 --> row1# col2 --> row2# 那么我们做如下操作，对矩阵按行反转，就像反转字符串那样#      |     |#  --- · --- · --- : row2#   -  |  -  |  -             行对称轴#  --- · --- · --- : row1#      |     |#    col1' col2'# 再进行矩阵转置#      |     |#  --- · --- · --- : col2'#   -  |  -  |  -             行对称轴#  --- · --- · --- : col1'#      |     |#    row2' row1'# (1)上下反转n = len(matrix)top, bottom = 0, n-1while top < bottom:matrix[top][:], matrix[bottom][:] = matrix[bottom][:], matrix[top][:]top += 1bottom -= 1# (2)沿主对角线进行T转置for i in range(0, n):for j in range(0, i):matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]

4. 矩阵置零

题目链接：矩阵置零 - leetcode
题目描述：
给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
题目归纳：
略

解题思路：
解法： 矩阵置零 - leetcode官方题解
(1) 解法1，建立两个标记数组。时间复杂度$O(mn)$，空间复杂度$O(m+n)$
(2) 解法2，使用两个标记变量。时间复杂度$O(mn)$，空间复杂度$O(1)$
(3) 解法3，使用一个标记变量。时间复杂度$O(mn)$，空间复杂度$O(1)$。该解法较难理解，且收益不高，暂未记录到本文中。

#解法1，建立两个标记数组。
class Solution:def setZeroes(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""# (1)建立两个标记数组，分别是行标记数组与列标记数组m = len(matrix)n = len(matrix[0])row = [False for _ in range(m)]col = [False for _ in range(n)]# (2)遍历1for i in range(m):for j in range(n):if matrix[i][j] == 0:row[i] = Truecol[j] = True# (2)遍历2for i in range(m):for j in range(n):if row[i] or col[j]:matrix[i][j] = 0

#解法2，使用两个标记变量。
class Solution:def setZeroes(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""# 解法2，用矩阵的第一行和第一列来替代方法1的两个标记数组# 但这样需要使用额外的两个标记变量，分别记录第一行和第一列是否原本就包含 0。# (1)首先预处理出两个标记变量# (2)使用其他行与列去处理第一行与第一列# (3)然后反过来使用第一行与第一列去更新其他行与列# (4)最后使用两个标记变量更新第一行与第一列# 上述过程类似于变量值交换，互相做过河的石头# (1)首先预处理出两个标记变量m = len(matrix)n = len(matrix[0])flag_col0 = any(matrix[i][0] == 0 for i in range(m))flag_row0 = any(matrix[0][j] == 0 for j in range(n))# (2)使用其他行与列去处理第一行与第一列for i in range(1,m):for j in range(1,n):if matrix[i][j] == 0:matrix[0][j] = 0 #第一行matrix[i][0] = 0 #第一列# (3)反过来使用第一行与第一列去更新其他行与列for i in range(1,m):for j in range(1,n):if matrix[i][0] == 0 or matrix[0][j] == 0:matrix[i][j] = 0# (4)最后使用两个标记变量更新第一行与第一列if flag_row0:for j in range(n):matrix[0][j] = 0if flag_col0:for i in range(m):matrix[i][0] = 0

5. 生命游戏

题目链接：生命游戏 - leetcode
题目描述：
根据 百度百科 ， 生命游戏 ，简称为 生命 ，是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。
给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态： 1 即为 活细胞 （live），或 0 即为 死细胞 （dead）。每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：
如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡；
如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活；
如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡；
如果死细胞周围正好有三个活细胞，则该位置死细胞复活；
下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态，返回下一个状态。
题目归纳：
略

解题思路：
解法： 生命游戏 - leetcode官方题解
(1) 新建数组。耗费内存空间
(2) 记录复合状态：-1, 0, 1, 2，并二次遍历。

Python

class Solution:def gameOfLife(self, board: List[List[int]]) -> None:"""Do not return anything, modify board in-place instead."""# (1)活细胞周围八个位置的活细胞数 < 2，    该位置活细胞死亡# (2)活细胞周围八个位置的活细胞数 =2 or 3，该位置活细胞仍然存活# (3)活细胞周围八个位置的活细胞数 > 3，    该位置活细胞死亡# (4)死细胞周围八个位置的活细胞数 = 3，    该位置死细胞复活；# (5)下一个状态，是通过将上述规则，同时应用于当前状态下的每个细胞，所形成的，其中细胞的出生和死亡是同时发生的。即你不能先更新某些格子，然后使用它们的更新后的值再更新其他格子，那还能原地修改吗？# (6)注意事项。原则上，面板是无限的，但当活细胞侵占了面板边界时会造成问题。# 这里不考虑非原地修改的算法，那样太浪费空间了，实际中肯定也不会那样使用# 使用额外的复合状态# -1:过去存活，现在死亡# 0:死亡# 1:存活# 2:过去死亡，现在存活# 由于复合状态隐含了过去细胞的状态，所以可以在不复制数组的情况下完成原地更新neighbors = [(1,0), (1,-1), (0,-1), (-1,-1), (-1,0), (-1,1), (0,1), (1,1)]rows = len(board)cols = len(board[0])# 一、遍历每个细胞并更新复合状态for row in range(rows):for col in range(cols):# (1)统计每个细胞的活邻居数live_neighbors = 0for neighbor in neighbors:# 相邻位置坐标r = row + neighbor[0]c = col + neighbor[1]# 邻居是否为活细胞if (0 <= r and r < rows) and (0 <= c and c < cols) and abs(board[r][c]) == 1: # -1或1都是过去存活live_neighbors += 1# (2)根据活邻居数应用规则if board[row][col] == 1 and (live_neighbors < 2 or 3 < live_neighbors):board[row][col] = -1if board[row][col] == 0 and live_neighbors == 3:board[row][col] = 2# 二、再次遍历，得到更新后的状态for row in range(rows):for col in range(cols):if board[row][col] > 0:board[row][col] = 1else:board[row][col] = 0

这篇关于Leetcod面试经典150题刷题记录 —— 矩阵篇的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---