本文主要是介绍Newto-Raphson,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
- Newton-Raphson
- 一阶形式
- 推导过程
- 二阶形式
- 推导过程
- 一阶形式
- Convex Function
- Quadratic Program
1. Newton-Raphson
解决 f(x)=0 问题的逼近方式
一阶形式
xnew=xold−f(x)f′(x)f′(x)=∂f(x)∂x
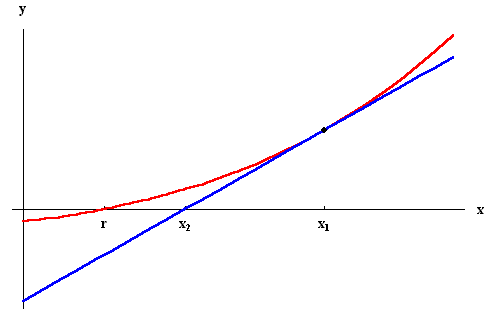
推导过程
1级泰勒展开:
f(x+Δx)=f(x)+Δxf′(x)
令 f(x+Δx)≈0 Δx 是x使得f(x)趋近于0的方向。那么
f(x)+Δxf′(x)=0→Δx=−f(x)f′(x)
二阶形式
xnew=xold−∇−2f(xold)×∇f(xold)
矩阵形式
xnew=xold−H−1∇f(xold)H=∇2f
H是Hessian Matrix.
推导过程
泰勒二级展开
f(X+ΔX)=f(X)+∇Tf(X)×ΔX+12(ΔX)T×∇2f(X)×ΔX
令 f(X+ΔX)=0→
ΔX=−(∇2f(X))−1×∇f(X)
ΔX 是X逼近解的方向。
Convex Function
Quadratic Program
F=xTAx+bTx+cxmax=−0.5A−1b
这篇关于Newto-Raphson的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!