本文主要是介绍Fourier transform笔记,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
https://www.youtube.com/watch?v=spUNpyF58BY
笔记
目录
- Fourier transform
- laplace transform
- FFT(快速傅里叶变换)
- DFT(离散傅里叶变换)
- 采样频率
- 理想情况
- 解决相的问题
- 真正的DFT
- FFT引入原因
- FFT原理
Fourier transform
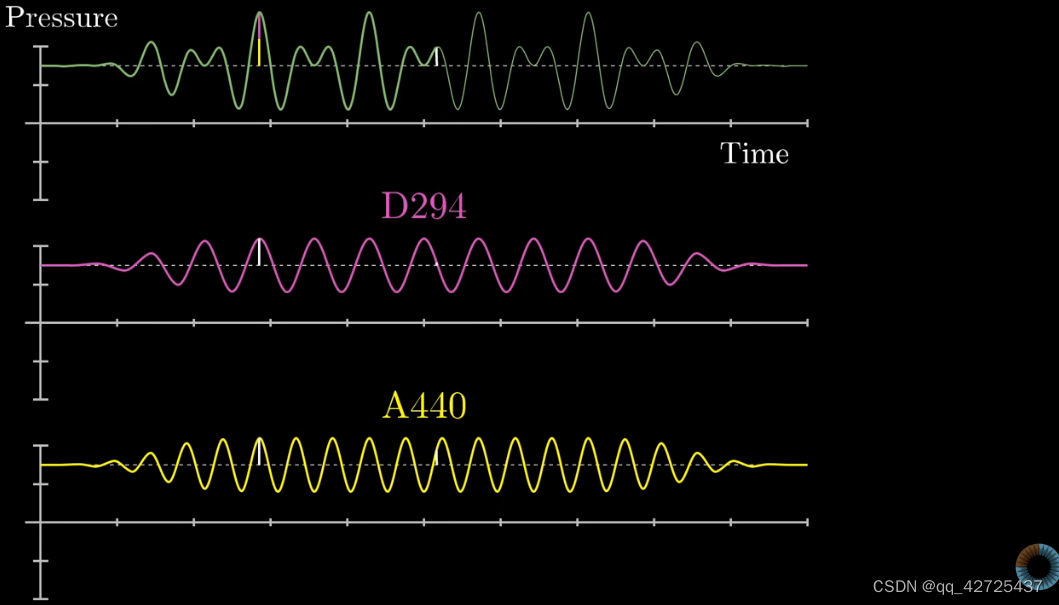
对于一个声音,可以把它拆解为多个正弦波,上面是两个正弦波组成的声波,但是当情况更复杂以后
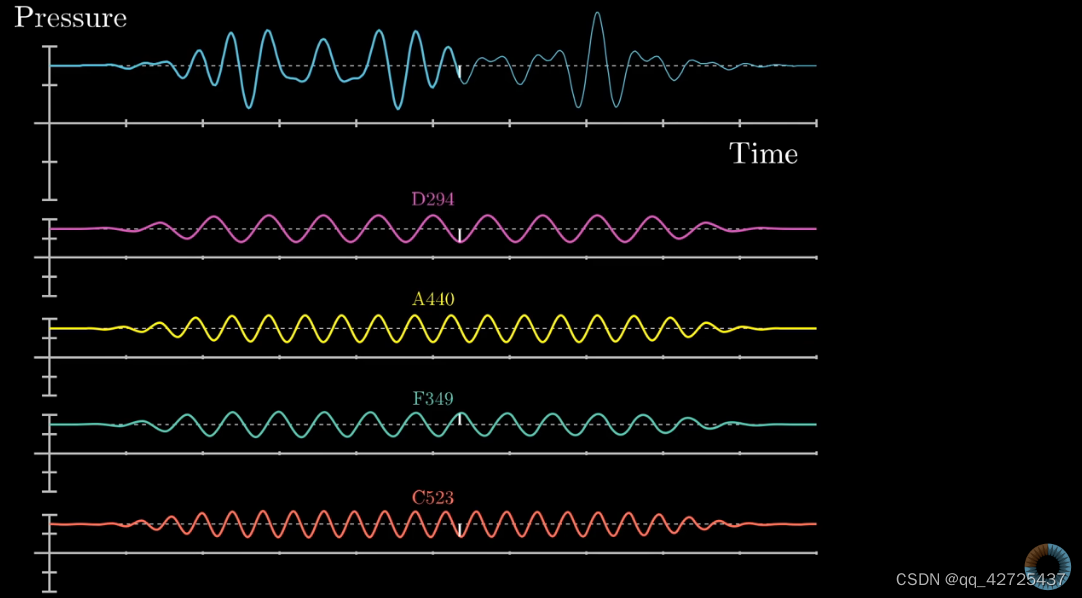
很难,从声波中提取出有用的信息,所以采用下面的方法
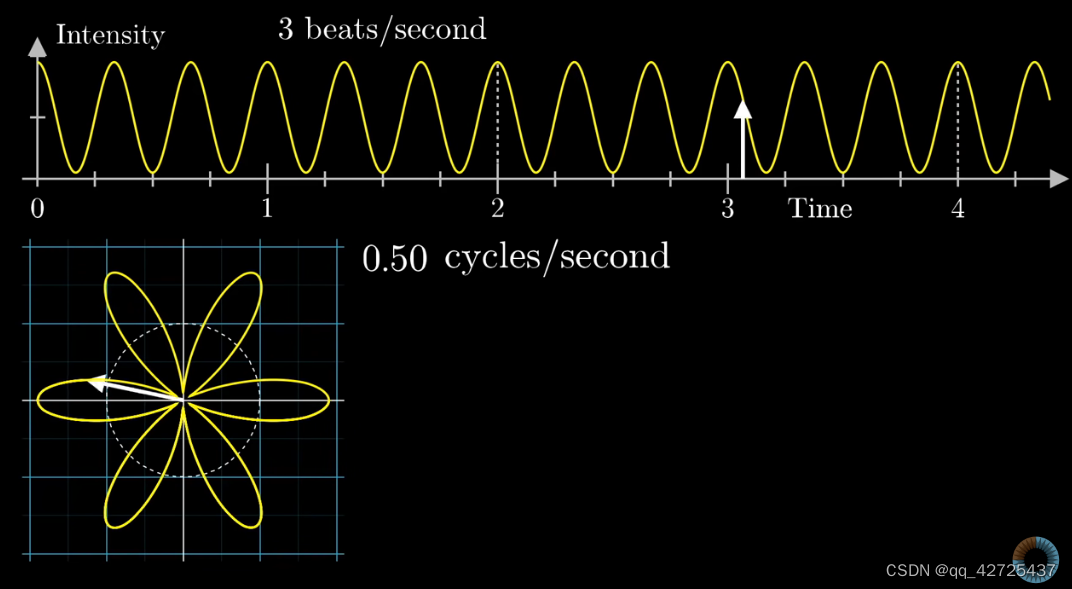
可以看到,将时间上的波形转换为了左下角的环形的波形,其中,与远点的距离与上面图中与时间轴相对应(白色箭头),图中,有两个频率,一个是时间上的频率,一秒内有3个beats,另一个是打包上图得到左下图的频率(图中虚线),这里是0.5c/s,也就是左下图旋转一周,时间上过了2s。不同的频率,得到的图是不同的。
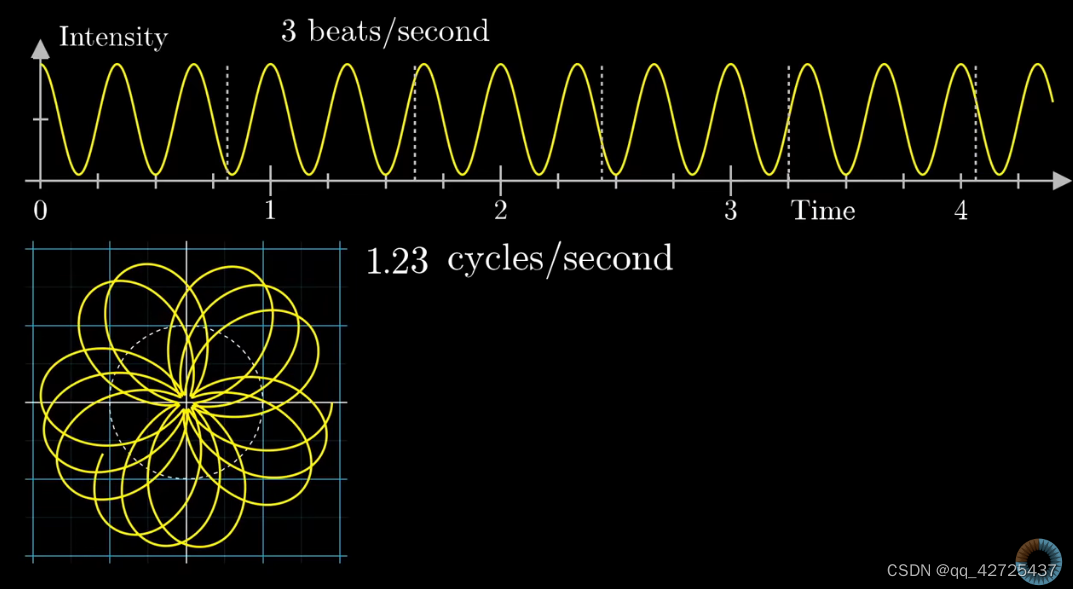
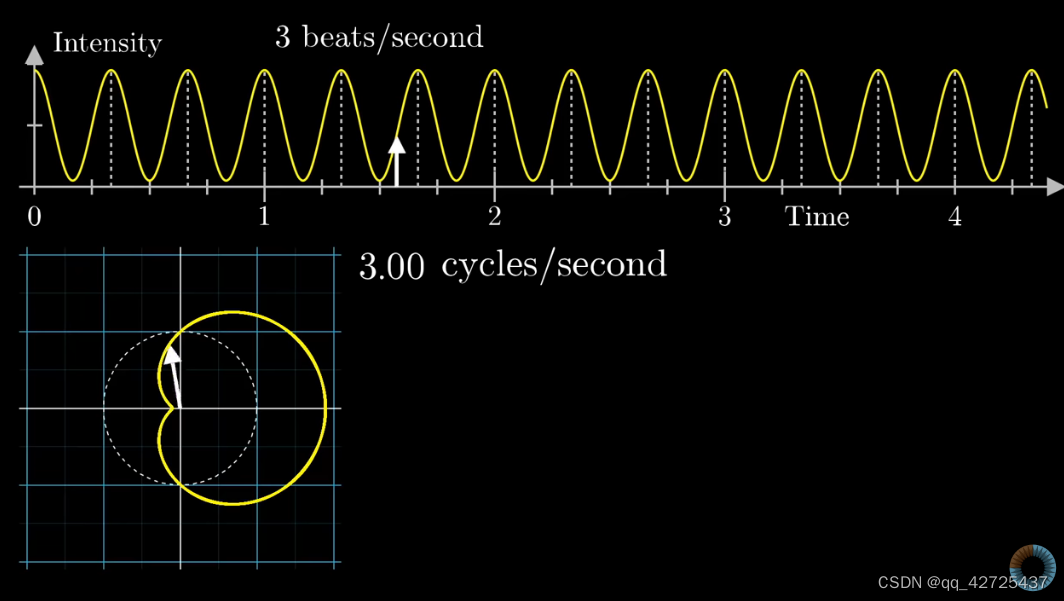
把左下图中的图形当作一个整体,得到质心,绘制出下图,其中右下图中的y轴是左下图质心的x轴坐标信息。
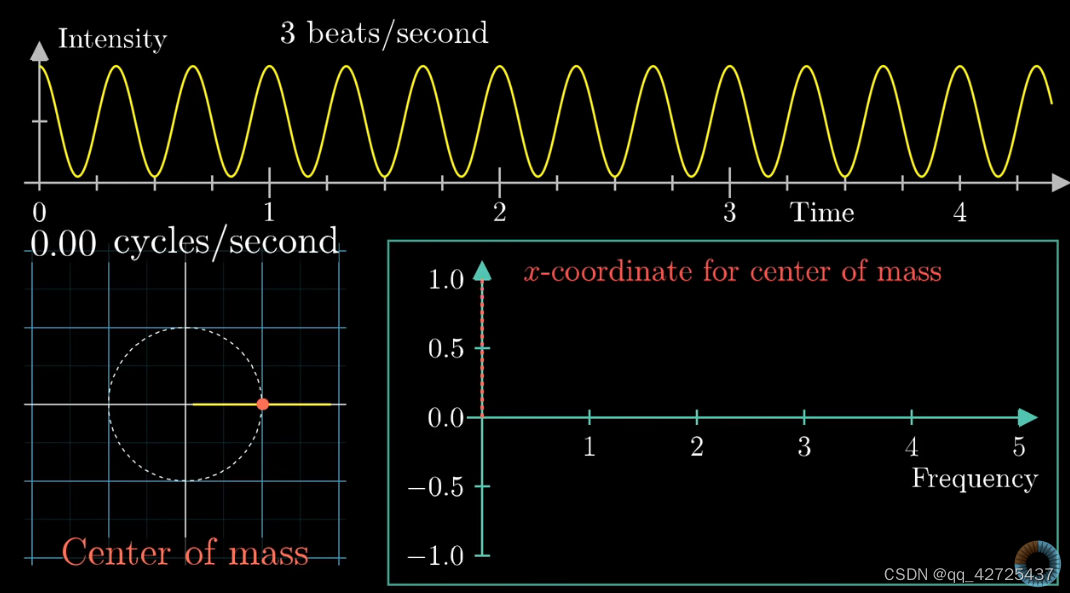
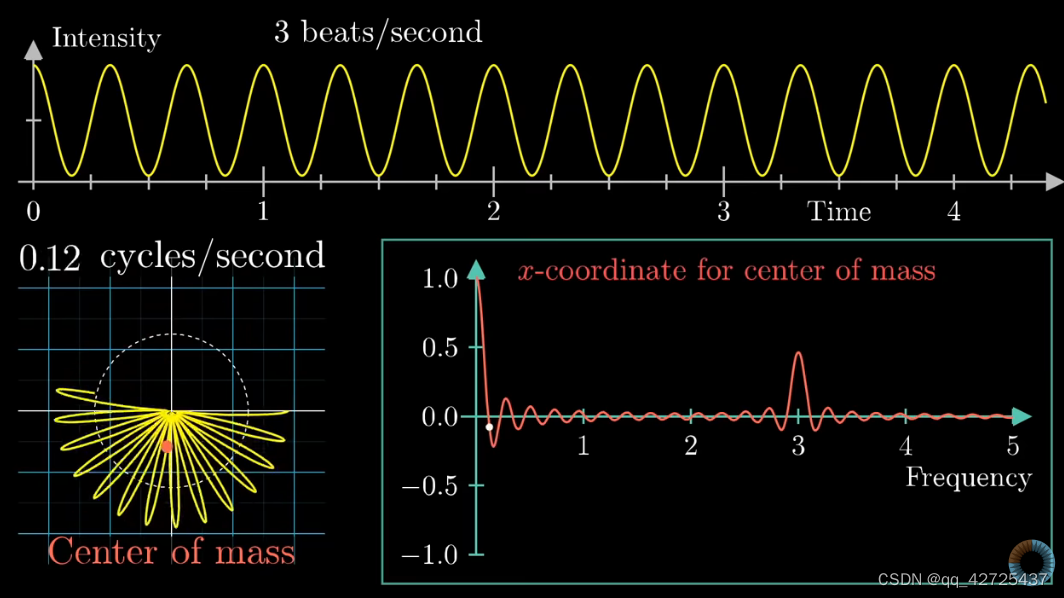
这样就得到了频域的信息,可以看到,在3明显突起,更改幅度,依然如此
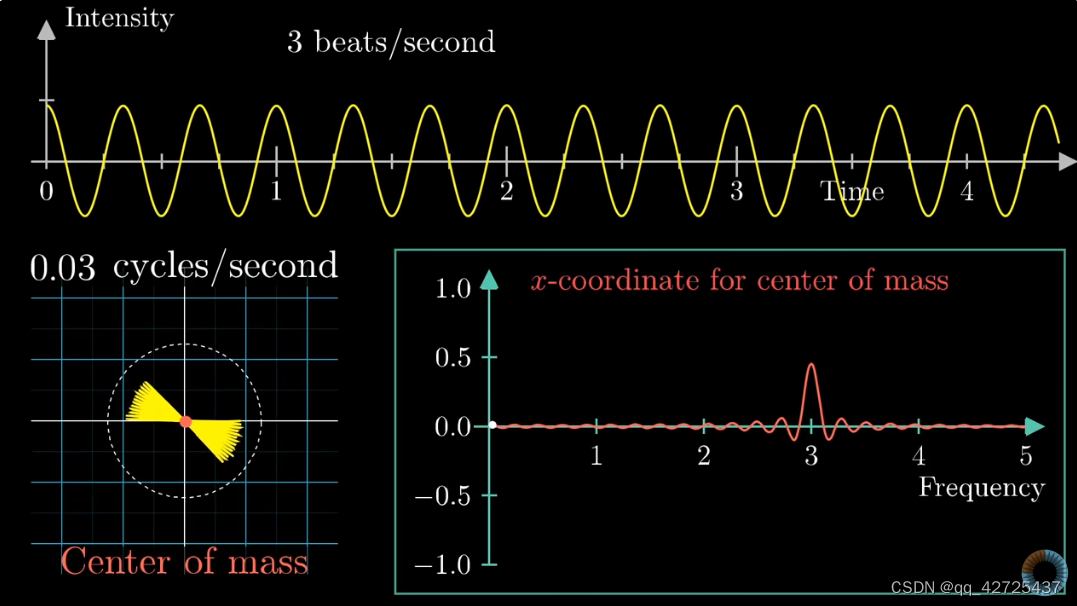
3正好是频率的值,这不是巧合,可以用它来分解波形
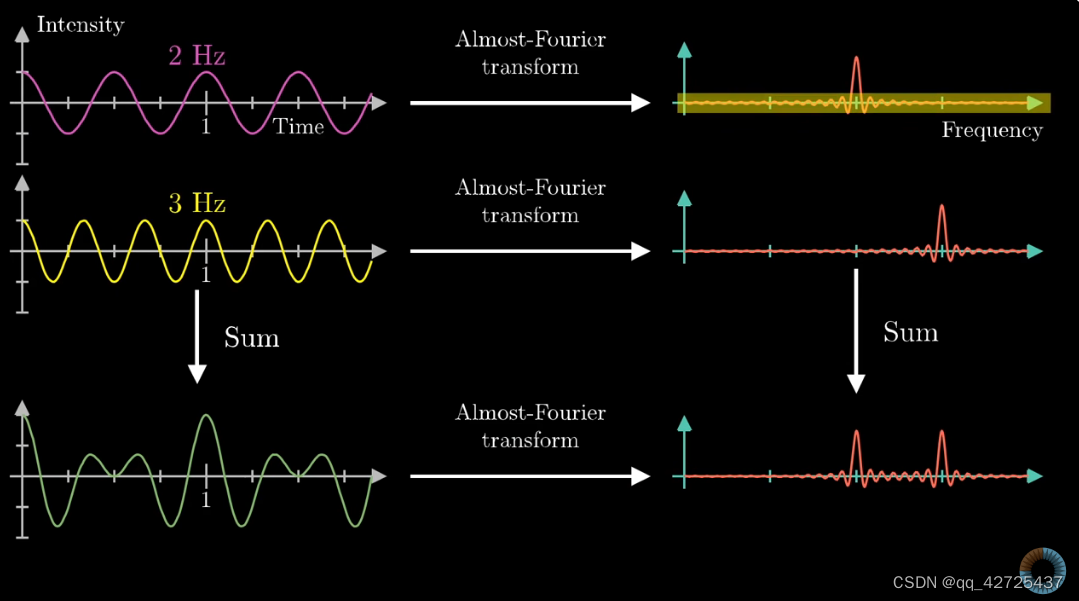
为什么是almost,是因为需要去掉高频信息
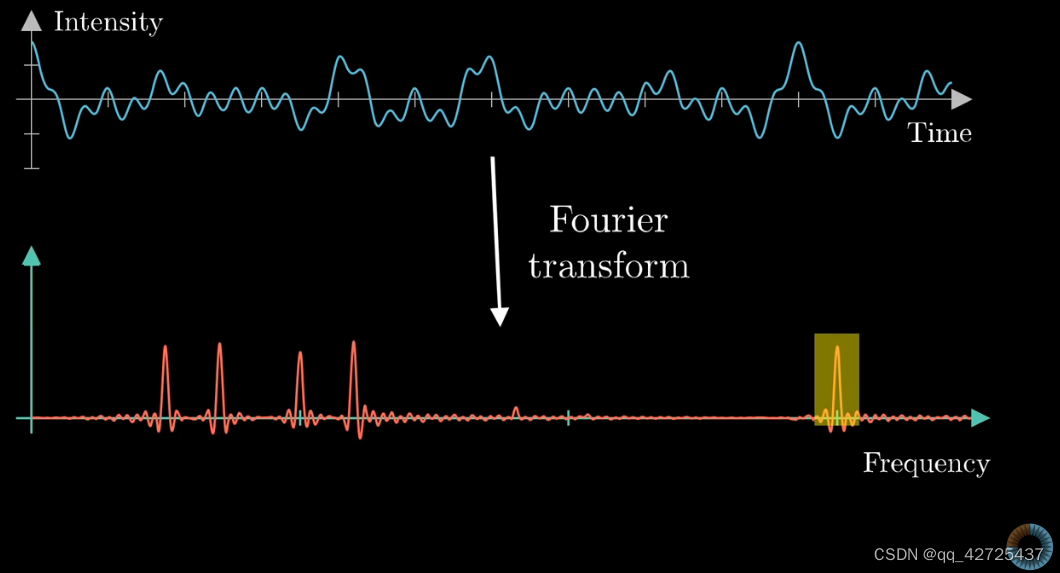
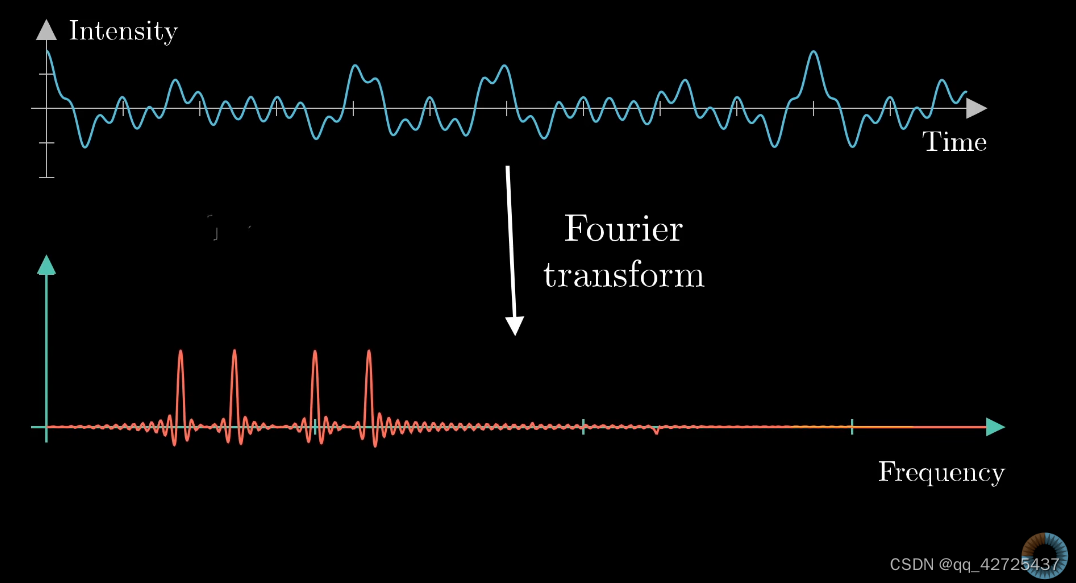
反向fourier transform,与正向的没有区别
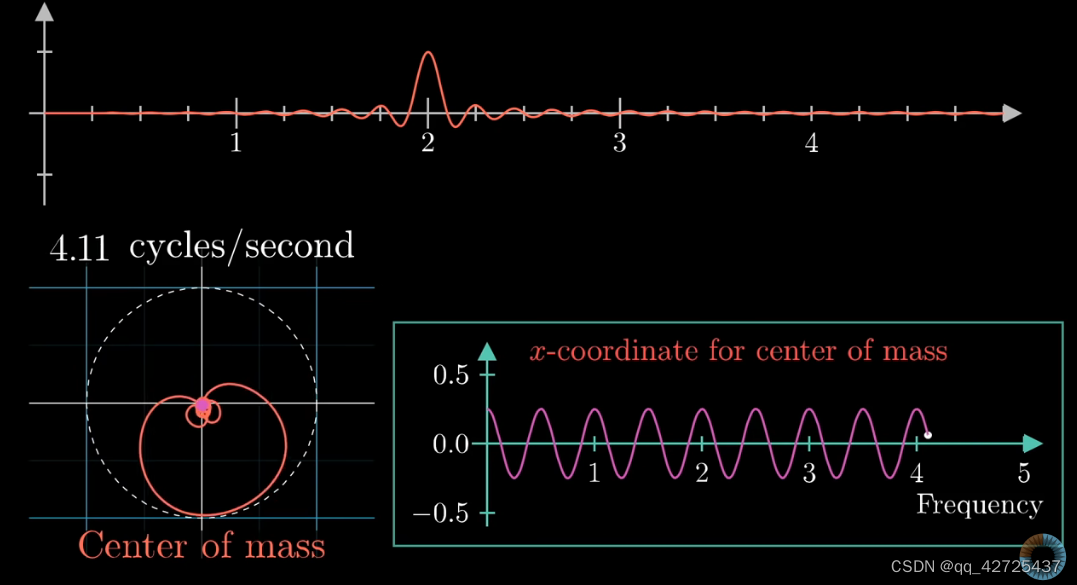
现在已经有了x轴上的fourier变换,需要考虑y轴,既然是二维,可以用复数域来解决。
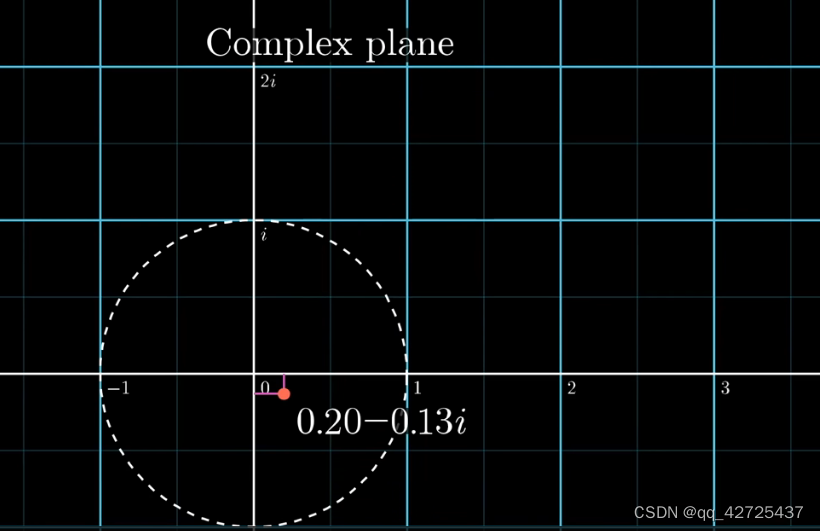
欧拉公式
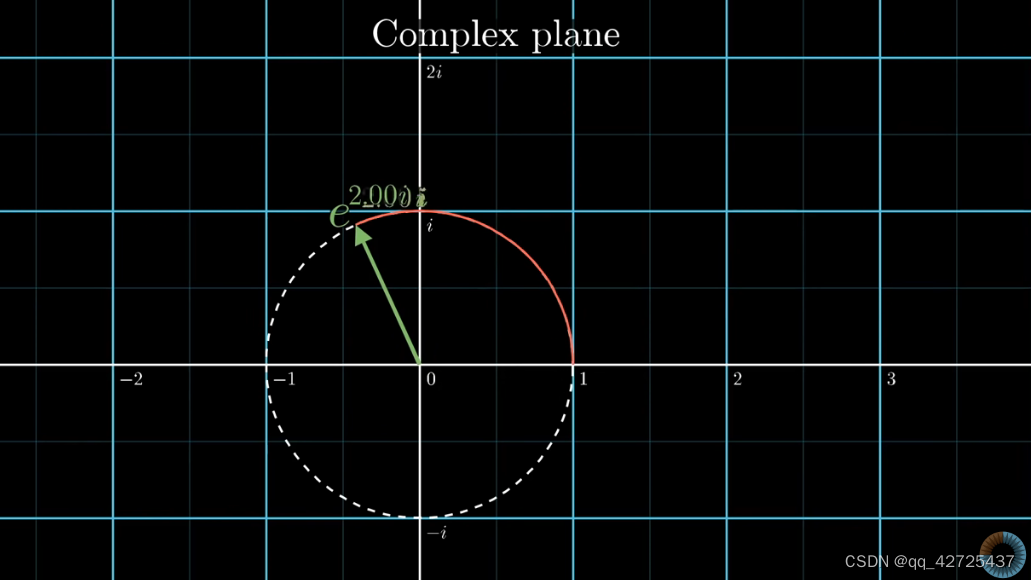
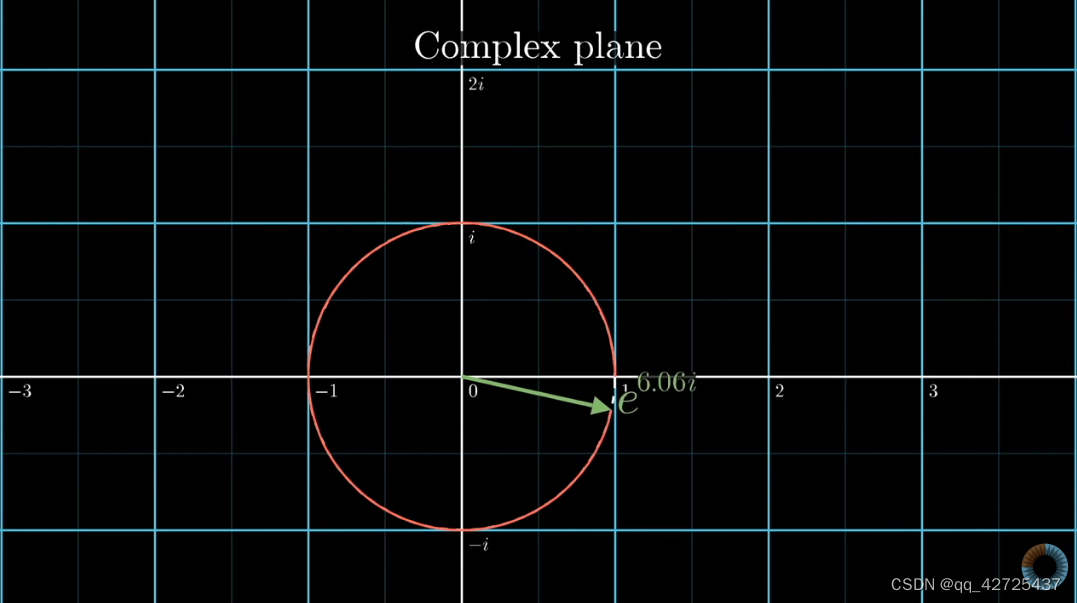
e 2 π i f t e^{2\pi ift} e2πift
其中,f是频率,t是时间,逆时针旋转,那么顺时针旋转
e − 2 π i f t e^{-2\pi ift} e−2πift
再乘以强度g(t),这就是我们需要的
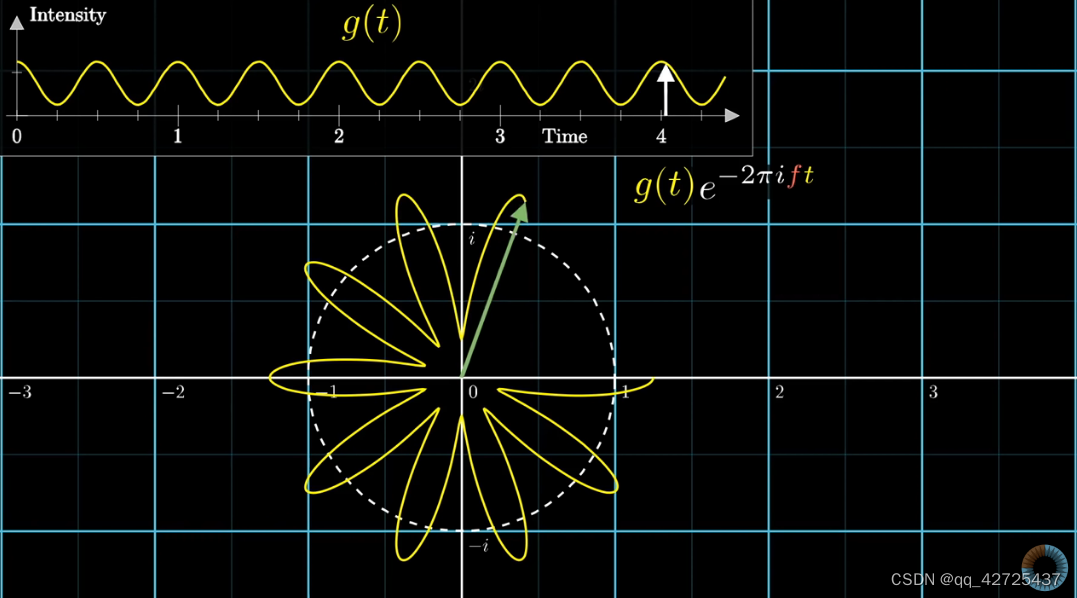
这样就得到了fourier变换公式,但多了 1 t 2 − t 1 \frac{1}{t_2-t_1} t2−t11,去掉这一部分就可以表示随着时间变化,质心与原点距离是变化的,不是一成不变的。
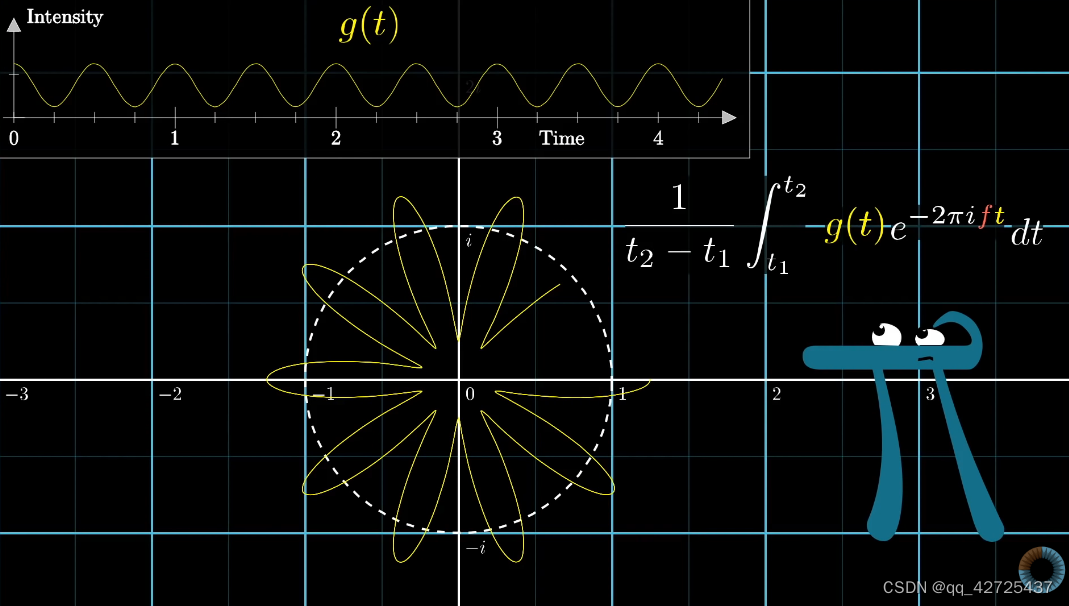
laplace transform

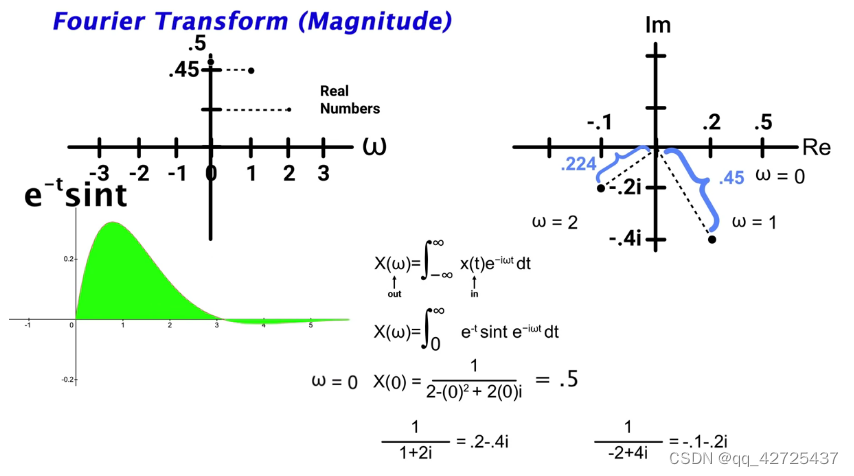
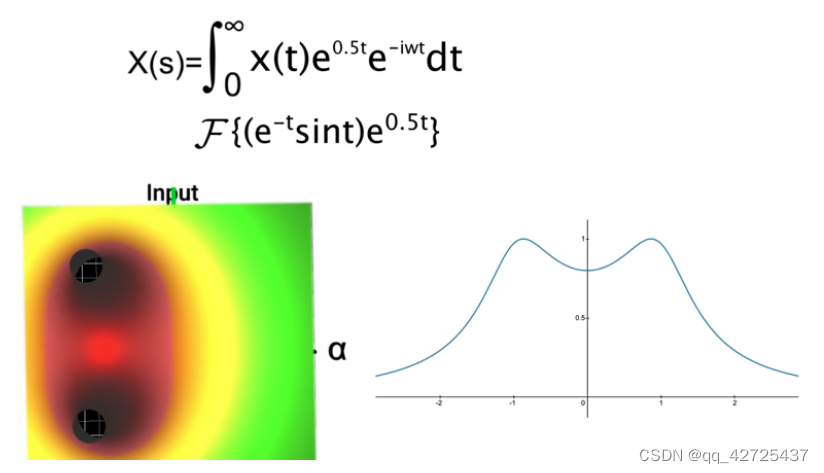
laplace变换就是对 e − t s i n t e^{-t}sint e−tsint的fourier变换
X ( ω ) = ∫ − ∞ ∞ x ( t ) e − i ω t d t X ( ω ) = ∫ 0 ∞ e − t s i n t e − i ω t d t X ( ω ) = 1 1 + ( 1 + i ω ) 2 X ( ω ) = 1 2 − ω 2 + 2 ω i X(\omega) = \int^{\infty}_{-\infty}x(t)e^{-i\omega t}dt \\ X(\omega) = \int^{\infty}_{0}e^{-t}sinte^{-i\omega t} dt \\ X(\omega) = \frac{1}{1+(1+i\omega)^2} \\ X(\omega) = \frac{1}{2-\omega^2 + 2\omega i} X(ω)=∫−∞∞x(t)e−iωtdtX(ω)=∫0∞e−tsinte−iωtdtX(ω)=1+(1+iω)21X(ω)=2−ω2+2ωi1
从第二个式子到第三个式子的推导如下
X ( ω ) = ∫ 0 ∞ e − t s i n t e − i ω t d t = − 1 1 + i ω ∫ 0 ∞ s i n t e − ( 1 + i ω ) t d ( − ( 1 + i ω ) t ) = − 1 1 + i ω s i n t e − ( 1 + i ω ) t ∣ 0 ∞ + − 1 1 + i ω ∫ 0 ∞ s i n t e − ( 1 + i ω ) t d t = − 1 1 + i ω ∫ 0 ∞ s i n t e − ( 1 + i ω ) t d t = − 1 ( 1 + i ω ) 2 c o s t e − ( 1 + i ω ) t ∣ 0 ∞ − − 1 ( 1 + i ω ) 2 ∫ 0 ∞ s i n t e − ( 1 + i ω ) t d t = 1 ( 1 + i ω ) 2 − − 1 ( 1 + i ω ) 2 ∫ 0 ∞ s i n t e − ( 1 + i ω ) t d t \begin{align} X(\omega) &= \int^{\infty}_{0}e^{-t}sinte^{-i\omega t}dt \nonumber \\ &= -\frac{1}{1+i\omega}\int^{\infty}_{0}sinte^{-(1+i\omega) t}d(-(1+i\omega) t) \nonumber \\ &= -\frac{1}{1+i\omega}sint e^{-(1+i\omega) t} |^{\infty}_{0}+ -\frac{1}{1+i\omega}\int^{\infty}_{0}sinte^{-(1+i\omega) t}dt \nonumber \\ &= -\frac{1}{1+i\omega}\int^{\infty}_{0}sinte^{-(1+i\omega) t}dt \nonumber \\ &= -\frac{1}{(1+i\omega)^2}cost e^{-(1+i\omega) t} |^{\infty}_{0} - -\frac{1}{(1+i\omega)^2}\int^{\infty}_{0}sinte^{-(1+i\omega) t}dt\nonumber \\ &= \frac{1}{(1+i\omega)^2}- -\frac{1}{(1+i\omega)^2}\int^{\infty}_{0}sinte^{-(1+i\omega) t}dt\nonumber \\ \end{align} X(ω)=∫0∞e−tsinte−iωtdt=−1+iω1∫0∞sinte−(1+iω)td(−(1+iω)t)=−1+iω1sinte−(1+iω)t∣0∞+−1+iω1∫0∞sinte−(1+iω)tdt=−1+iω1∫0∞sinte−(1+iω)tdt=−(1+iω)21coste−(1+iω)t∣0∞−−(1+iω)21∫0∞sinte−(1+iω)tdt=(1+iω)21−−(1+iω)21∫0∞sinte−(1+iω)tdt

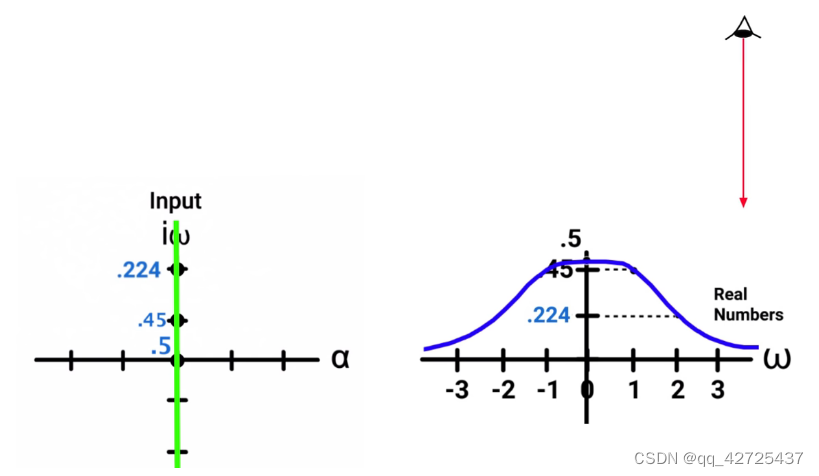
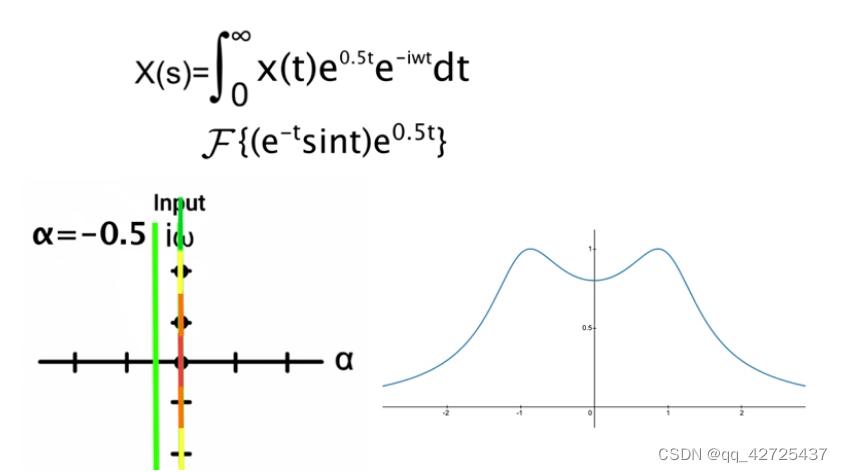
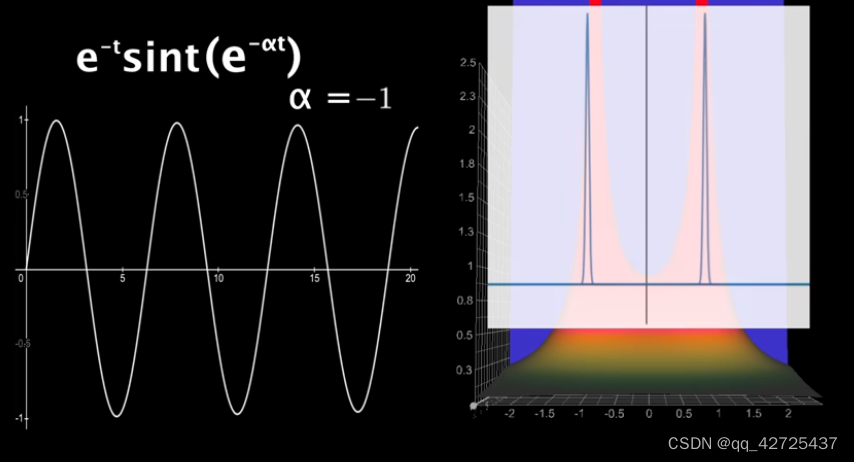
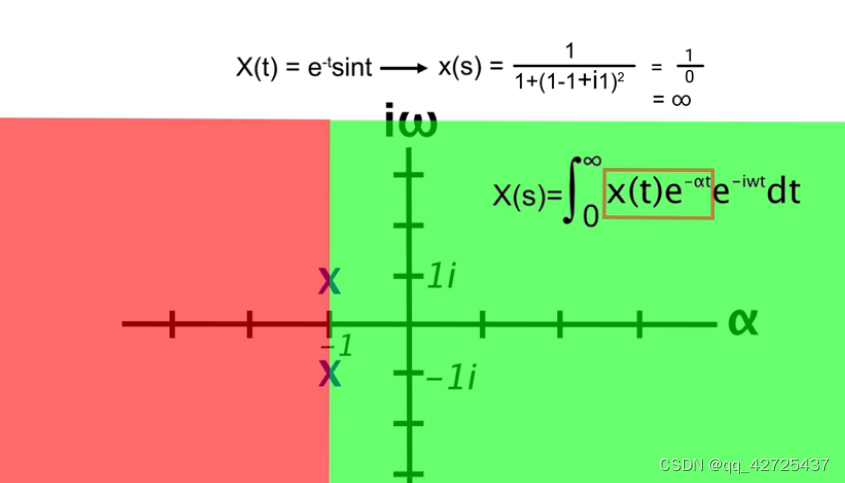
很明显, ω \omega ω控制正弦频率, α \alpha α控制指数衰减
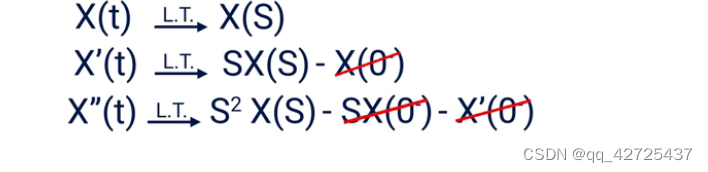
证明如下:
∫ 0 ∞ x ′ ( t ) e − s t d t = x ( t ) e − s t ∣ 0 ∞ + s ∫ 0 ∞ e − s t x ( t ) d t = s x ( s ) − x ( 0 ) \begin{align} \int^{\infty}_{0}x'(t)e^{-st}dt&=x(t)e^{-st}|^{\infty}_{0} + s\int^{\infty}_{0}e^{-st}x(t)dt \nonumber \\ &= sx(s)-x(0) \nonumber \end{align} ∫0∞x′(t)e−stdt=x(t)e−st∣0∞+s∫0∞e−stx(t)dt=sx(s)−x(0)
所以laplace变换可以用来求解常微分方程(ODEs)
FFT(快速傅里叶变换)
FFT是DFT的计算方法,首先了解DFT
DFT(离散傅里叶变换)
实际上就是将积分表示为离散的加和形式
X [ k ] = ∑ n = 0 N − 1 x n ⋅ e − i 2 π N k n X[k] = \sum^{N-1}_{n=0}x_n\cdot e^{\frac{-i2\pi}{N}kn} X[k]=n=0∑N−1xn⋅eN−i2πkn
其中,k是频率,总共有N个采样节点,n代表第n个点。
表示为矩阵形式就是:
[ X 0 , X 1 , X 2 , ⋯ , X N − 1 ] ⏞ 1 × N = [ x 0 , x 1 , x 2 , ⋯ , x N − 1 ] ⏞ 1 × N [ k = 0 k = 1 k = 2 ⋯ k = N − 1 ↓ ↓ ↓ ↓ ] ⏞ N × N \overbrace{[X_0, X_1, X_2, \cdots, X_{N-1}]}^{1\times N} = \overbrace{[x_0, x_1, x_2, \cdots, x_{N-1}]}^{1\times N} \overbrace{\begin{bmatrix} k=0 & k=1 & k=2 & \cdots & k=N-1\\ \Bigg\downarrow & \Bigg\downarrow & \Bigg\downarrow & & \Bigg\downarrow \end{bmatrix}}^{N \times N} [X0,X1,X2,⋯,XN−1] 1×N=[x0,x1,x2,⋯,xN−1] 1×N k=0↓ ⏐k=1↓ ⏐k=2↓ ⏐⋯k=N−1↓ ⏐ N×N
如果N很小的时候,这个矩阵乘法是容易计算的,但是现实中,对于信号常常有成百上千的采样点,那么计算量就非常大了,所以就需要FFT。
举例:有8个采样点,用不同频率的正弦函数去得到对应频率的值,每一个值是一个bin
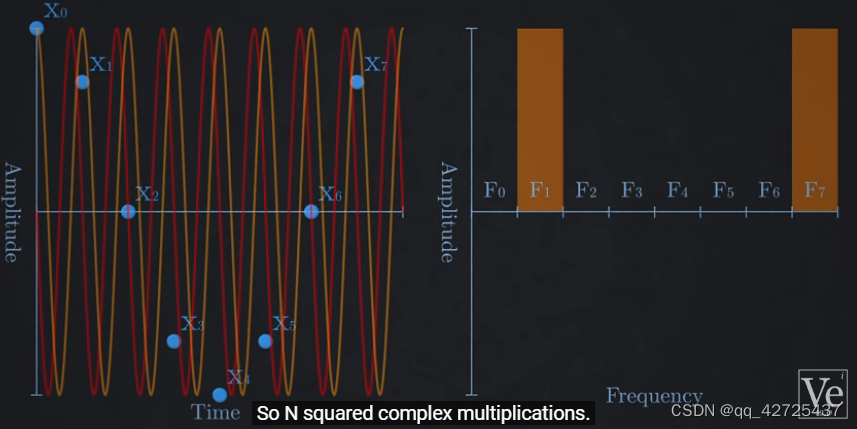
下面需要理解DFT为什么这么做,以及它面临的一些问题
采样频率
首先,根据nyquist定理,要采样频率为f的信号,需要2f+1的采样点,人耳能听到的最高频声音是20khz,所以现实中采样率一般为44.1khz
理想情况
假设有一个f=2hz的余弦,那么我就希望在频域中2的位置有峰值,其他位置为0
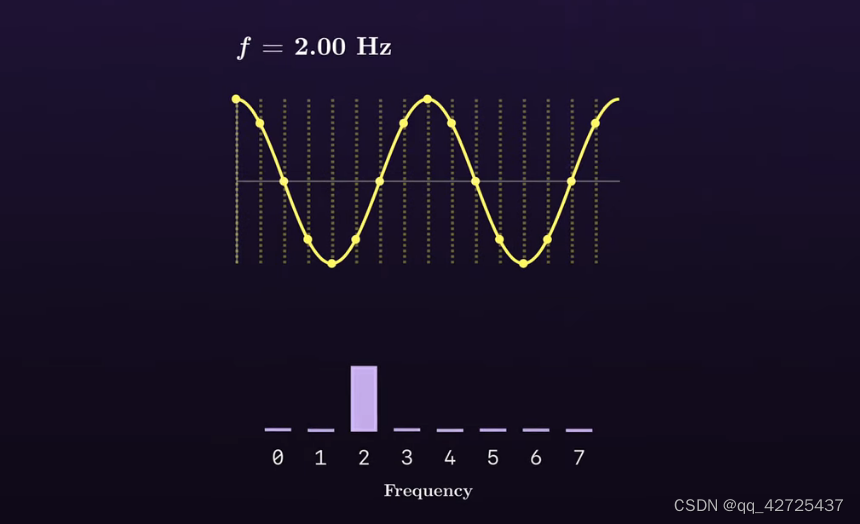
那就将离散化得到的向量与不同频率下的波形去求相似性,如果相似度高,就代表该频率下有峰值,这也就是为什么DFT是有效的,意味着采样率一定等于最大频率(N=N)。
但是,通过计算不同频率的波的相似性,会发现问题, a 1 ⃗ = a 7 ⃗ \vec{a_1}=\vec{a_7} a1=a7, a 2 ⃗ = a 6 ⃗ \vec{a_2}=\vec{a_6} a2=a6等,导致右下图中很多值不为0
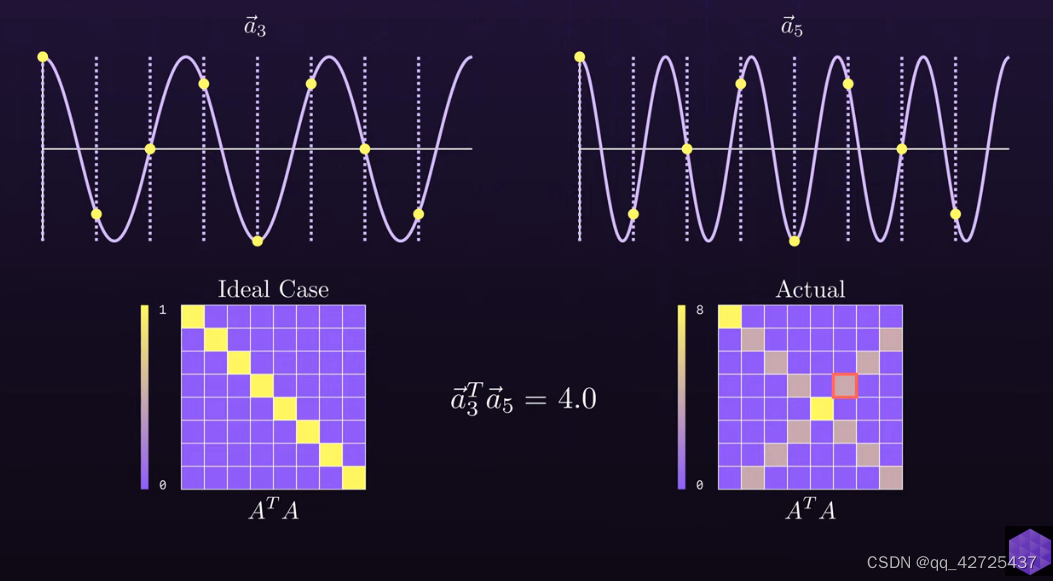
也就是A矩阵不仅不正交,还不可逆,所以不是DFT的最终版本
但是可以发现右下图的左上角这一部分是可逆的,所以每次都采样双倍,但只是采用其中的前半部分。
解决相的问题
通过之前的解决方案,无论是改变幅度,还是频率,或者是初始值,都可以实现FT的功能,但是,当改变相位的时候,频域中的值受到影响,这是不正确的。这是因为在这个变化过程中,无论是sin还是cos都会存在为0的情况,所以要将两者组合在一起。
真正的DFT
就是为sin和cos分别保存一个矩阵,合并后,就得到了我们开始的时候DFT的公式。
FFT引入原因
利用避免重复计算来提升计算速度,上图需要进行64个复数域乘法,改进后,只需要计算24个
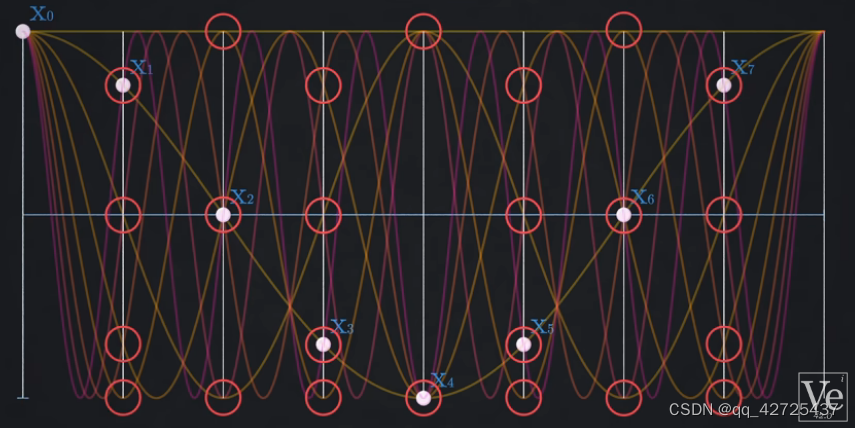
FFT原理
对DFT中的部分用W表示,方便表达

简单来讲就是数学家利用上面提到的旋转因子W的周期性,对称性等性质进行公式化简。在算法编程中则是不断利用已经计算过的点来算新的点,即:旧点算新点。
FFT需要依赖蝶形图进行计算
X ( k ) = ∑ n = 0 N − 1 x ( n ) W N n k = ∑ n = 0 , 2 , 4 , ⋯ N − 1 x ( n ) W N n k + ∑ n = 1 , 3 , 5 ⋯ N − 1 x ( n ) W N n k → 令n=2r = ∑ r = 0 , 1 , ⋯ N 2 − 1 x ( 2 r ) W N 2 r k + ∑ r = 0 , 1 , ⋯ N 2 − 1 x ( 2 r + 1 ) W N ( 2 r + 1 ) k → x ( 2 r ) = x 1 ( r ) = ∑ r = 0 , 1 , ⋯ N 2 − 1 x 1 ( r ) W N 2 r k + ∑ r = 0 , 1 , ⋯ N 2 − 1 x 2 ( r ) W N ( 2 r + 1 ) k → W N ( 2 r + 1 ) k = W N k ∗ W N / 2 r k W N 2 r k = W N / 2 r k = ∑ r = 0 , 1 , ⋯ N 2 − 1 x 1 ( r ) W N / 2 r k + W N k ∑ r = 0 , 1 , ⋯ N 2 − 1 x 2 ( r ) W N / 2 ( r k ) = X 1 ( k ) + W N k X 2 ( k ) \begin{align} X(k) &= \sum^{N-1}_{n=0}x(n)W_N^{nk} \nonumber \\ &= \sum^{N-1}_{n=0,2,4,\cdots}x(n)W_N^{nk} + \sum^{N-1}_{n=1, 3, 5\cdots}x(n)W_N^{nk} \xrightarrow{\text{令n=2r}}\nonumber \\ &= \sum^{\frac{N}{2}-1}_{r=0,1,\cdots}x(2r)W_N^{2rk} + \sum^{\frac{N}{2}-1}_{r=0,1, \cdots}x(2r+1)W_N^{(2r+1)k} \xrightarrow{x(2r)=x_1(r)}\nonumber \\ &= \sum^{\frac{N}{2}-1}_{r=0,1,\cdots}x_1(r)W_N^{2rk} + \sum^{\frac{N}{2}-1}_{r=0,1, \cdots}x_2(r)W_N^{(2r+1)k} \xrightarrow[W_N^{(2r+1)k} = W_{N}^{k} * W_{N/2}^{rk}]{W_N^{2rk}=W_{N/2}^{rk}}\nonumber \\ &= \sum^{\frac{N}{2}-1}_{r=0,1,\cdots}x_1(r)W_{N/2}^{rk} + W_N^k\sum^{\frac{N}{2}-1}_{r=0,1, \cdots}x_2(r)W_{N/2}^{(rk)} \nonumber \\ &=X_1(k)+W_N^kX_2(k) \nonumber \end{align} X(k)=n=0∑N−1x(n)WNnk=n=0,2,4,⋯∑N−1x(n)WNnk+n=1,3,5⋯∑N−1x(n)WNnk令n=2r=r=0,1,⋯∑2N−1x(2r)WN2rk+r=0,1,⋯∑2N−1x(2r+1)WN(2r+1)kx(2r)=x1(r)=r=0,1,⋯∑2N−1x1(r)WN2rk+r=0,1,⋯∑2N−1x2(r)WN(2r+1)kWN2rk=WN/2rkWN(2r+1)k=WNk∗WN/2rk=r=0,1,⋯∑2N−1x1(r)WN/2rk+WNkr=0,1,⋯∑2N−1x2(r)WN/2(rk)=X1(k)+WNkX2(k)
上面的过程没有减少运算量继续进行简化
∵ X ( k ) = ∑ r = 0 , 1 , ⋯ N 2 − 1 x 1 ( r ) W N / 2 r k ∴ X 1 ( k + N / 2 ) = ∑ r = 0 , 1 , ⋯ N 2 − 1 x 1 ( r ) W N / 2 r ( k + N / 2 ) = ∑ r = 0 , 1 , ⋯ N 2 − 1 x 1 ( r ) W N / 2 r k = X 1 ( k ) \because X_(k) = \sum^{\frac{N}{2}-1}_{r=0,1,\cdots}x_1(r)W_{N/2}^{rk} \\ \therefore X_1(k+N/2) = \sum^{\frac{N}{2}-1}_{r=0,1,\cdots}x_1(r)W_{N/2}^{r(k+N/2)}=\sum^{\frac{N}{2}-1}_{r=0,1,\cdots}x_1(r)W_{N/2}^{rk} = X_1(k) ∵X(k)=r=0,1,⋯∑2N−1x1(r)WN/2rk∴X1(k+N/2)=r=0,1,⋯∑2N−1x1(r)WN/2r(k+N/2)=r=0,1,⋯∑2N−1x1(r)WN/2rk=X1(k)
同理, X 2 ( k + N / 2 ) = X 2 ( k ) X_2(k+N/2) = X_2(k) X2(k+N/2)=X2(k)
∵ X ( k ) = X 1 ( k ) + W N k X 2 ( k ) ∴ X ( k + N / 2 ) = X 1 ( k + N / 2 ) + W N k + N / 2 X 2 ( k + N / 2 ) → W N k + N / 2 = − W N k = X 1 ( k + N / 2 ) + W N k X 2 ( k + N / 2 ) = X 1 ( k ) − W N k X 2 ( k ) \because X(k)=X_1(k)+W_N^kX_2(k) \\ \therefore \begin{align} X(k+N/2)&=X_1(k+N/2)+W_N^{k+N/2}X_2(k+N/2) \xrightarrow{W_N^{k+N/2}=-W_N^k} \nonumber \\ &= X_1(k+N/2)+W_N^{k}X_2(k+N/2) = X_1(k)-W_N^kX_2(k) \nonumber \end{align} ∵X(k)=X1(k)+WNkX2(k)∴X(k+N/2)=X1(k+N/2)+WNk+N/2X2(k+N/2)WNk+N/2=−WNk=X1(k+N/2)+WNkX2(k+N/2)=X1(k)−WNkX2(k)
综上推导得到:
X ( k ) = X 1 ( k ) + W N k X 2 ( k ) X ( k + N / 2 ) = X 1 ( k ) − W N k X 2 ( k ) X(k)=X_1(k)+W_N^kX_2(k) \\ X(k+N/2) = X_1(k)-W_N^kX_2(k) X(k)=X1(k)+WNkX2(k)X(k+N/2)=X1(k)−WNkX2(k)
这里都是用X1和X2来计算,所以缩减了计算量
继续推导
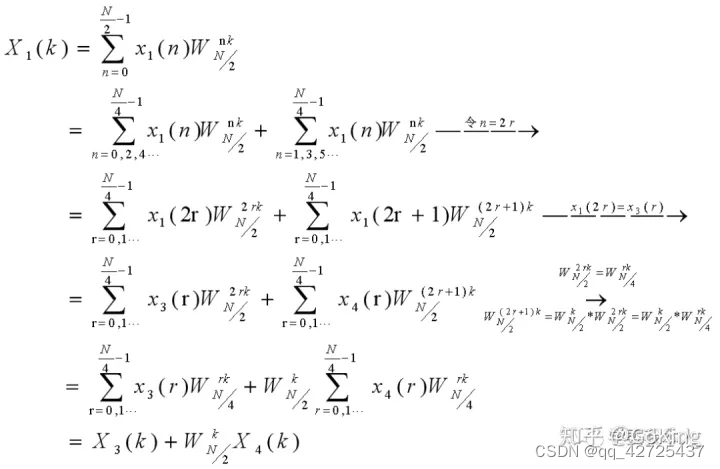
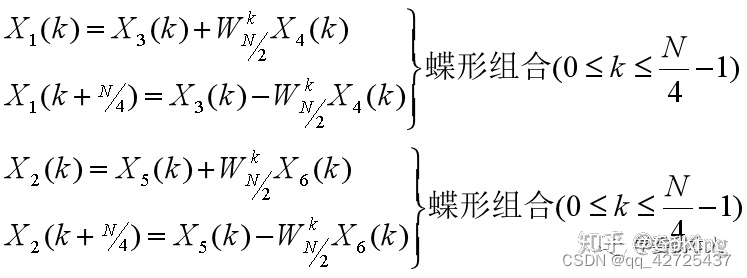
最后一步
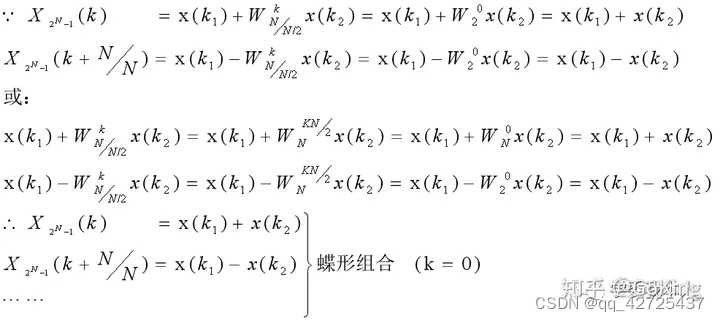
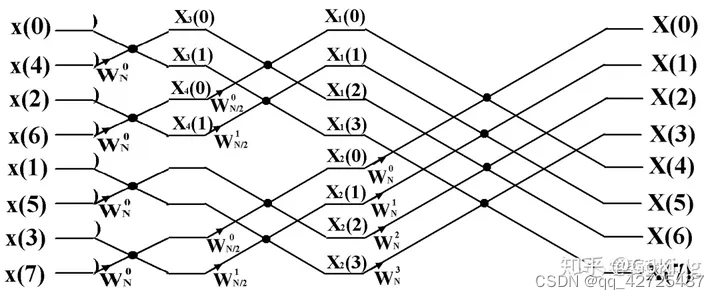
这篇关于Fourier transform笔记的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






