本文主要是介绍算法通关村第十四关—堆结构(青铜),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
堆结构
一、堆的概念和特征
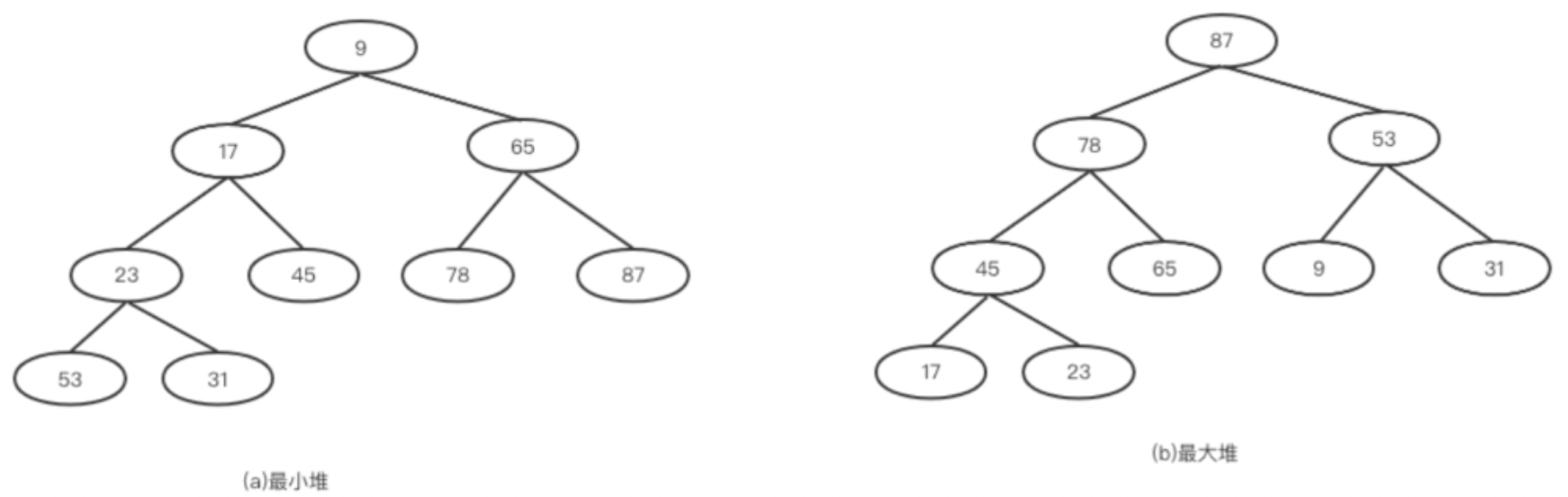
堆是将一组数据按照完全二叉树的存储顺序,将数据存储在一个一维数组中的结构。堆有两种结构,一种称为大顶堆,一种称为小顶堆,如下图。
1.小顶堆:任意节点的值均小于等于它的左右孩子,并且最小的值位于堆顶,即根节点处
2.大顶堆:任意节点的值均大于等于它的左右孩子,并且最大的值位于堆顶,即根节点处。
有些地方也叫大根堆、小根堆,或者最大堆、最小堆。大和小的特征等都是类似的。
二、堆的构造过程
这里先假设一个节点的下标为:
1、当i=0时,为根节点。
2、当i>=1时,父节点为(i-1)/2。
size就是元素的个数,从1开始计数。
下面就看一下如何建立一个大堆:
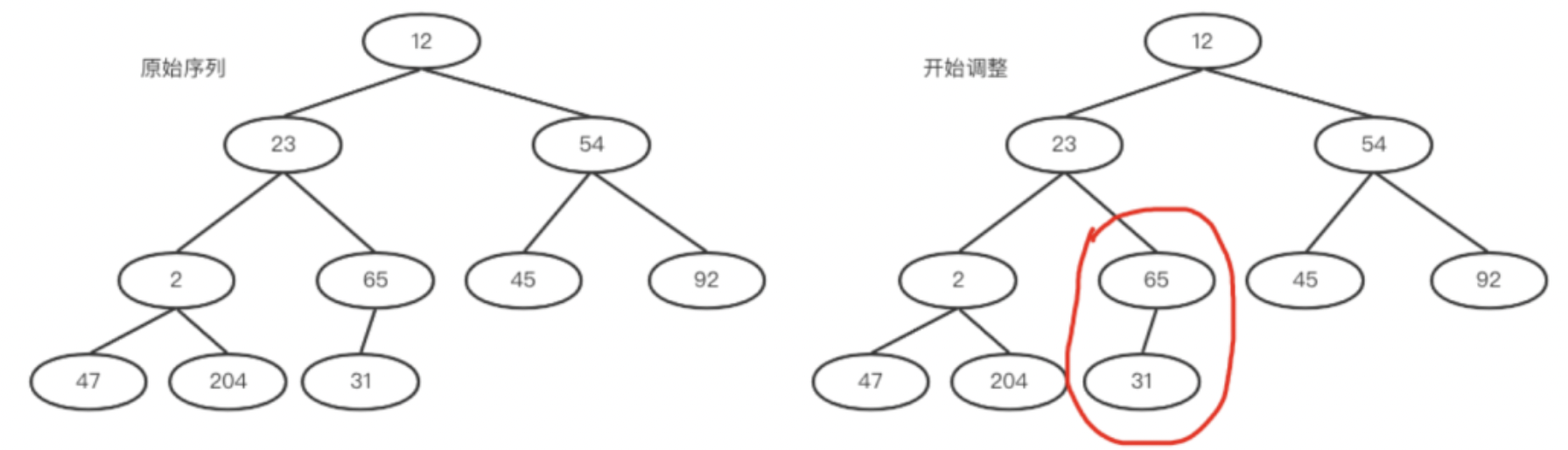
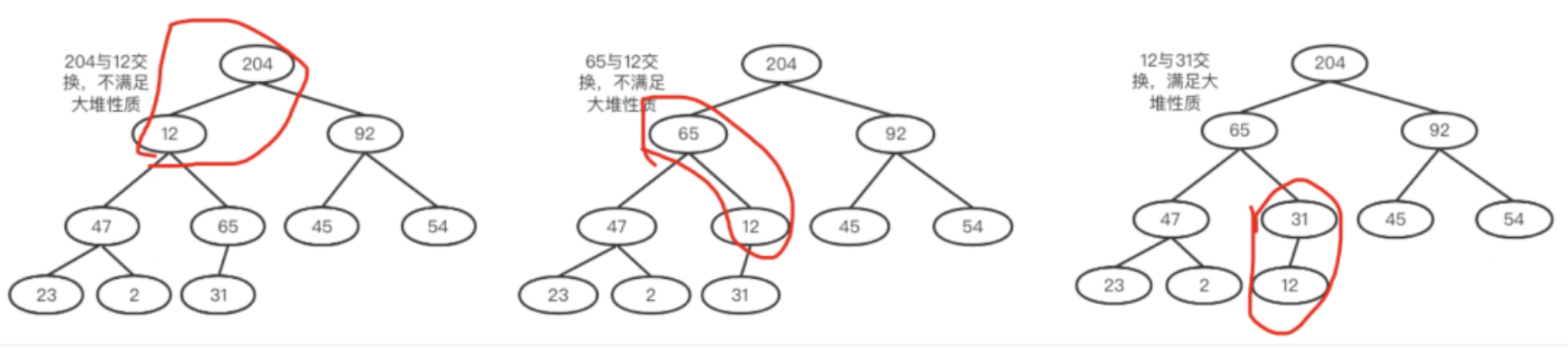
将元素依次排到完全二叉树节点上去,如下左图所示。
a.int i = (size-2)/2 = 4(思考一下这里为什么是size-2而不是size-1)。找到数组中的4号下标。
65大于其孩子,满足大堆性质,所以不用交换。如下右图
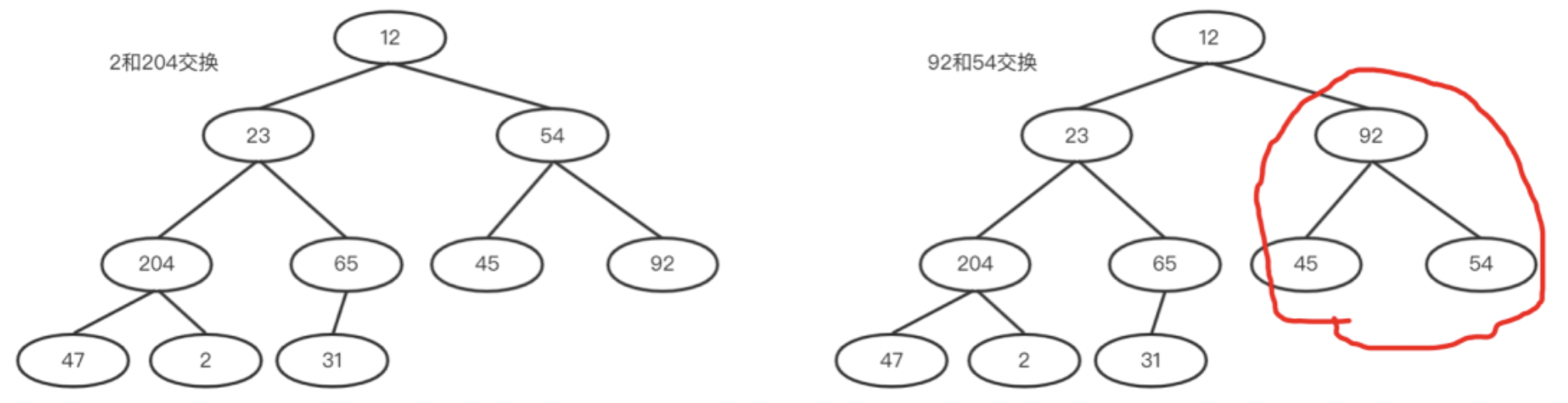
b.然后i=i-1;然后用2和其孩子比较,2和204交换。交换之后204所在的子树满足大堆,如下左图。
c.54和其孩子比较,54和92交换。此时92所在子树满足大堆,如下右图。
d.继续,23和其孩子比较,23和204交换,交换完之后,23的子树却不满足了,所以还需调整它的子树。如下两图所示。
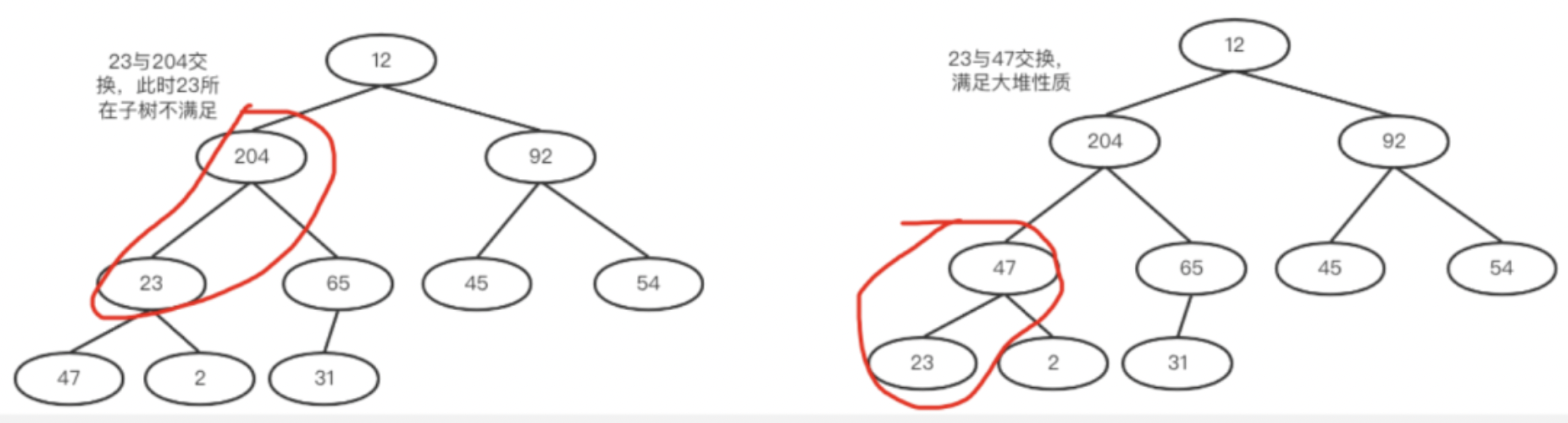
e.12和204交换,仍然出现不平衡衡的情况,以此类推,直到根节点也满足要求就完毕了
这样我们就建好了一个大顶堆,从图中可以看到,根元素是整个树中值最大的那个,而第二大和第三大就是其左右子树,具体是哪个更大则是未知的,需要比较一下才知道。
三、插入操作
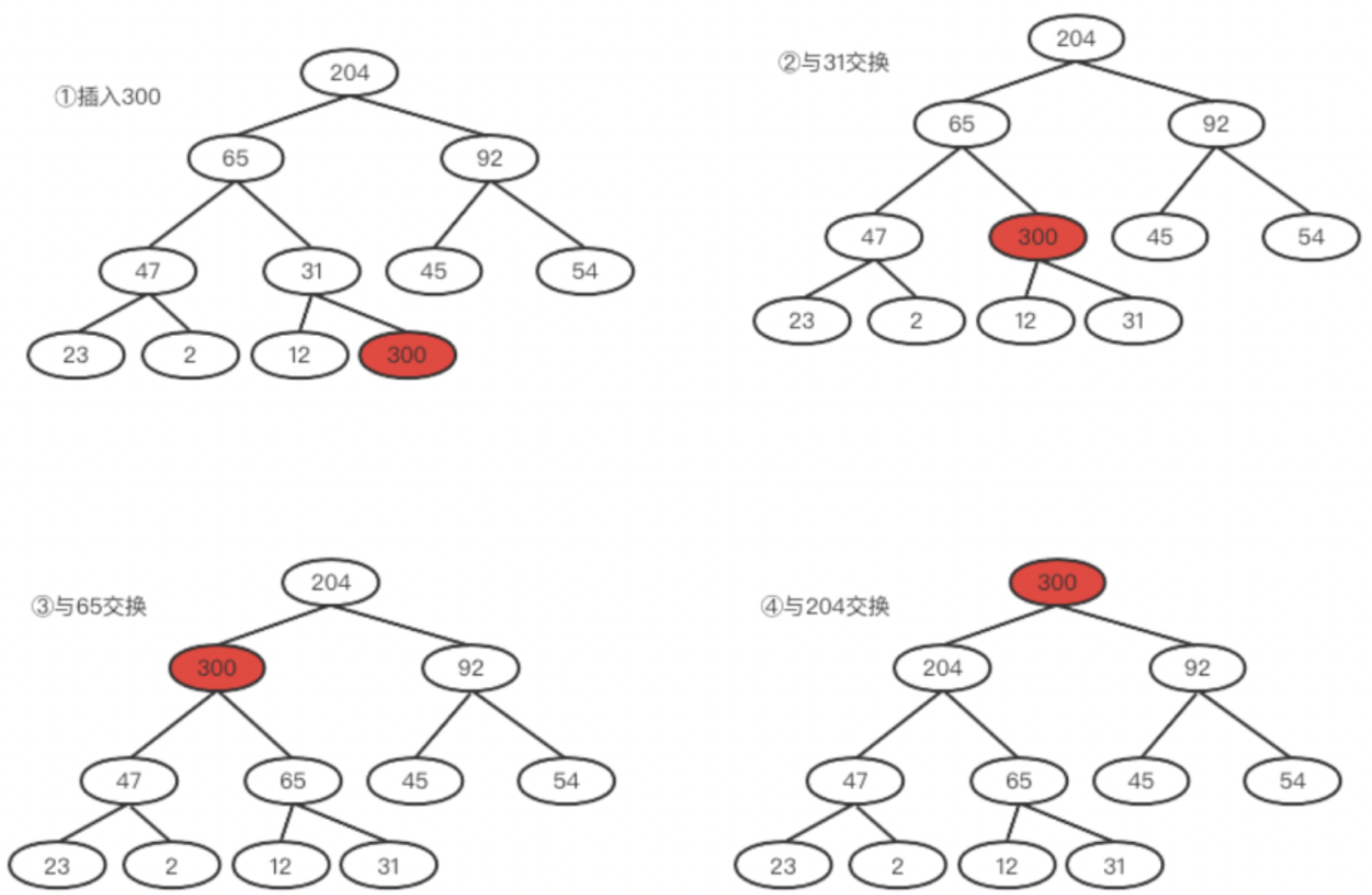
从上面可以看到根节点和其左右子节点是堆里的老大老二和老三,其他结点则没有太明显的规律,那如果要插入一个新元素,该怎么做呢?直接说规则,将元素插入到保持其为完全二叉树的最后一个位置,然后顺着这条支路一直向上调整,每前进一层就要保证其子树都满足堆否则测就去处理子树,直到完全满足要求。
看一个例子,如下图,要插入300,我们将其插入到31的右孩子位置,然后不断向上爬,31<300,所以两者要交换,再向上发现300比65大,所以两者要交换。最后300比根元素204大,两者也交换。最后就得到了新的堆。完整过程如下所示:
四、删除操作
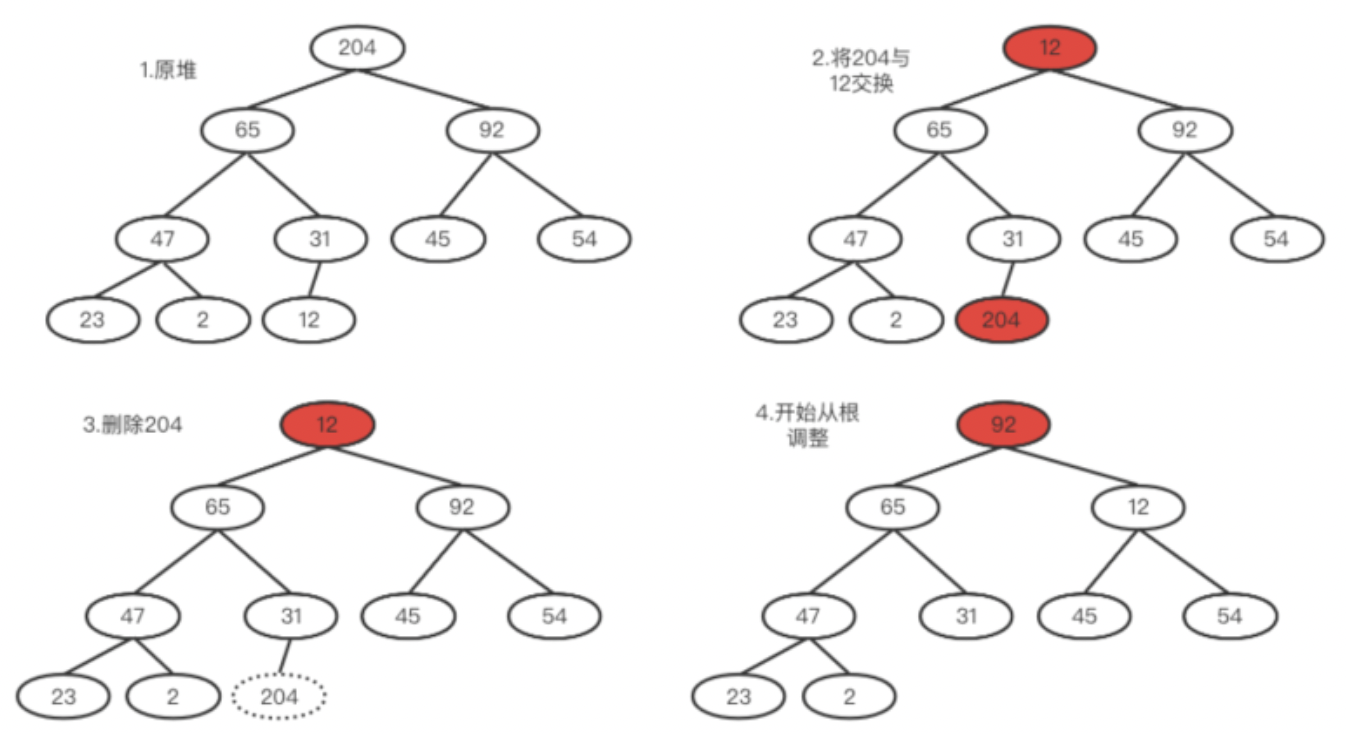
堆本身比较特殊,一般对堆中的数据进行操作都是针对堆顶的元素,即每次都从堆中获得最大值或最小值,其他的不关心,所以我们删除的时候,也是删除堆顶。但如果直接删掉堆顶,整个结构被破坏了。
所以实际策略是先将堆中最后一个元素(假如为A)和堆顶元素进行替换,然后删除堆中最后一个元素。之后再从根开始逐步与左右比较,谁更大谁上位。然后A再继续与子树比较,如果有更大的继续交换,直到自己所在的子树也满足大顶堆。
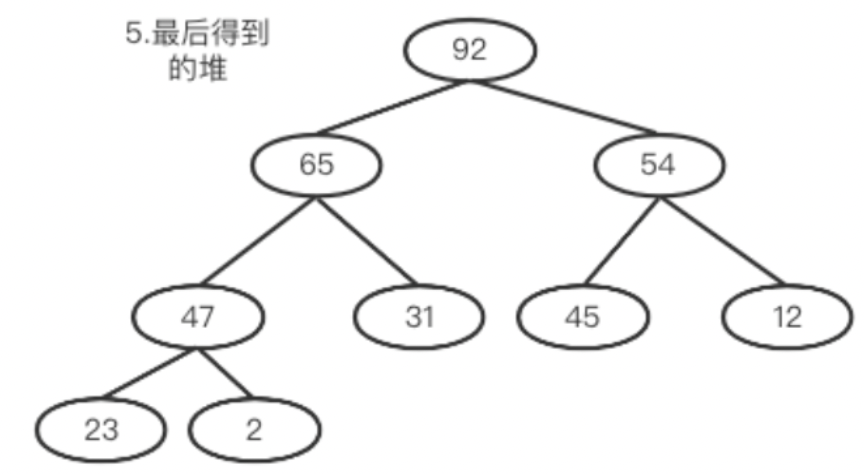
最后新的堆结构如下:
总结
堆的价值就在于大顶堆的根节点是整个树最大的那个,增加时会根据根的大小来决定要不要加,而删除操作只删除根元素。这个特征可以在很多场景下有奇妙的应用,后面的算法题全都基于这一点。
这里可能有些人还有疑问,感觉不管插入还是删除,堆的操作都不简单,那为什么还说堆的效率比较高呢?
这是因为堆元素的数量是有限制的,一般不用将所有的元素都放到堆里。后面题目中可以看到,在序列中找K大,则堆的大小就是K。如果K个链表合并,那么堆就是K。原理后面详细展开。
关于堆的问题,记住口诀:
1.查找:找大用小,大的进;找小用大,小的进。
2.排序:升序用小,降序用大。
查找的口诀解释一下就是:是找K大,则用小堆,后续数据只有比根元素更大时才允许进入堆。如果是找K小,则对应反过来。
这篇关于算法通关村第十四关—堆结构(青铜)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






