本文主要是介绍管理类联考——数学——真题篇——按题型分类——充分性判断题——蒙猜C,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
老规矩,先看目录,平均每个3-4C(C是月饼,月饼一般分为4块)
C是什么,是两个都不行了,但联合起来可以,联合的英文是combined,好的,我知道这个英文也记不住,或者ABC都是对一个,A是条件(1)√,B是条件(2)√,C就是条件(1)+(2)√。
C是combined联合的意思,那么,取值范围有交集(交集也算另一种联合);一个等号和一个不等号需要合作,一个定性和一个定量需要一起分析(常言道需要不同角度分析事物)
文章目录
- 2023-2013真题
- 2023
- 真题(2023-17)-C-单一条件信息不完全,选C;
- 真题(2023-18)-C-选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D
- 真题(2023-23)-C-一个等号+一个不等号,一个定性+一个定量,选C(定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意));
- 真题(2023-24)-C-一个等号+一个不等号,一个定性+一个定量,选C(定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意));
- 2022
- 真题(2022-18)-C-要素列表法-固有关系-知三推四-总体分为甲乙两部分:①甲部分均值;②乙部分均值;③总体均值;④甲乙三间比例。这四个量中知道三个可求得第四个;
- 真题(2022-24)-C-整体规律+局部特例:大规律在前,局部特例在后,且整体规律不能代表局部特例,选C;
- 真题(2022-25)-C-选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D
- 2021
- 真题(2021-16)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意);-C-要素列表法plus:-固有关系-知三推四-总体分为甲乙两部分:①甲部分均值;②乙部分均值;③总体均值;④甲乙三间比例。这四个量中知道三个可求得第四个;
- 真题(2021-18)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
- 真题(2021-19)-C-特值体系法-两项特值与三项特值;-要素列表法plus-特殊套路-所有圆半径,球半径,均设为需要通过勾股定理求解;即要确定两个要素,需要两个关系;
- 真题(2021-24)-C-一个等号+一个不等号,一个定性+一个定量,选C(定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意));
- 2020
- 真题(2020-17)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
- 真题(2020-18)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
- 真题(2020-19)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
- 2019
- 真题(2019-16)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
- 真题(2019-19)-C-两选项出现取值范围,判断是否有交集⇒有交集选C⇒无交集选A
- 真题(2019-23)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
- 2018
- 真题(2018-22)-C-选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D
- 2017
- 真题(2017-18)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
- 真题(2017-23)-C-选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D
- 真题(2017-24)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
- 2016
- 真题(2016-17)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
- 真题(2016-19)-C-特值法-两变量不等关系中的特值法
- 真题(2016-22)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
- 2015
- 真题(2015-22)-C
- 真题(2015-24)-C-一个等号+一个不等号,一个定性+一个定量,选C(定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意));-C-整体规律+局部特例:大规律在前,局部特例在后,且整体规律不能代表局部特例,选C;-不同量选项秒杀-准确率90%-C:一个等号一个不等号(如a>0)或者一个定量一个定性(a为正数),选C;-C-几何-立体几何-圆柱体
- 真题(2015-25)-C-一个等号+一个不等号,一个定性+一个定量,选C(定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意));-C选项蒙猜-整体规律+局部特例:整体规律+局部特例:大规律在前,局部特例在后,且整体规律不能代表局部特例,选C;
- 2014
- 真题(2014-18)-C-一个等号+一个不等号,一个定性+一个定量,选C(定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意));
- 真题(2014-22)-C-单一条件信息不完全,首选C;-要素列表法与维度思维;
- 真题(2014-23)-C-一个等号+一个不等号,一个定性+一个定量,选C(定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意));-C-比较类问题要联合,首选C;
- 真题(2014-24)-C-本身条件差得远,但大前提限制为整数/自然数,导致可以充分;
- 2013
- 真题(2013-21)-C-单一条件信息不完全,选C;-C-必联立选项秒杀-准确率75%-C:条件1与条件2必须联立,选C。(25%选E);-C-算术-绝对值-绝对值三角不等式
- 真题(2013-22)-C-单一条件信息不完全,选C;
2023-2013真题
2023
真题(2023-17)-C-单一条件信息不完全,选C;
-C-代数-一元二次方程-举反例;


真题(2023-18)-C-选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D
-数列-等比数列


真题(2023-23)-C-一个等号+一个不等号,一个定性+一个定量,选C(定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意));
-C-应用题-植树;

(1)各班植树的棵树均不相同;“≠”为不等式
(2)各班植树棵树最大值是28;“=”等式

真题(2023-24)-C-一个等号+一个不等号,一个定性+一个定量,选C(定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意));
-数列-等比数列

(1)>是不等式;(2)为属性。

2022
真题(2022-18)-C-要素列表法-固有关系-知三推四-总体分为甲乙两部分:①甲部分均值;②乙部分均值;③总体均值;④甲乙三间比例。这四个量中知道三个可求得第四个;
-E-应用题-十字交叉法-画叉字,大量上,小量下,中量中,交叉减,差相除,同量比(大量减中量的差与中量减大量的差之比等于其量比,其中,中量可以是平均值,混合值;量比可以是数量比,质量比)
18.两个人数不等的班数学测验的平均分不相等,则能确定人数多的班。
(1)己知两个班的平均成绩。
(2)己知两个班的总平均值。


真题(2022-24)-C-整体规律+局部特例:大规律在前,局部特例在后,且整体规律不能代表局部特例,选C;
-C-数列-等差数列-判定+已知递推公式求 a n a_n an
24.已知正数列{ a n a_n an},则{ a n a_n an}是等差数列
(1) a n + 1 2 − a n 2 = 2 n , n = 1 , 2 , . . . a_{n+1}^2-a_n^2=2n,n=1,2,... an+12−an2=2n,n=1,2,...【整体规律(整体递推关系)】
(2) a 1 + a 3 = 2 a 2 a_1+a_3=2a_2 a1+a3=2a2【局部特例】



真题(2022-25)-C-选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D
-A-算术-绝对值-三角不等式-绝对值不等式的证明,通常先举反例排除明显错误的选项,再使用三角不等式或不等式的性质进行证明。
25.设实数𝑎,𝑏满足 ∣ a − 2 b ∣ ≤ 1 |a−2b|≤1 ∣a−2b∣≤1,则 ∣ a ∣ > ∣ b ∣ |a|>|b| ∣a∣>∣b∣
(1) ∣ b ∣ > 1 |b|>1 ∣b∣>1
(2) ∣ b ∣ < 1 |b|<1 ∣b∣<1

2021
真题(2021-16)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意);-C-要素列表法plus:-固有关系-知三推四-总体分为甲乙两部分:①甲部分均值;②乙部分均值;③总体均值;④甲乙三间比例。这四个量中知道三个可求得第四个;
-应用题-十字交叉-画叉字,大量上,小量下,中量中,交叉减,差相除,同量比(大量减中量的差与中量减大量的差之比等于其量比,其中,中量可以是平均值,混合值;量比可以是数量比,质量比)
16.某班增加两名同学。则该班同学的平均身高增加了。
(1)增加的两名同学的平均身高与原来男同学的平均身高相同。
(2)原来男同学的平均身高大于女同学的平均身高。


真题(2021-18)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
-应用题-比例-特值法
18.某单位进行投票表决,已知该单位的男女员工人数之比为3:2,则能确定是至少有50%的女员工参加了投票。
(1)赞成投票的人数超过了总人数的40%。
(2)参加投票的女员工比男员工多。
真题(2021-19)-C-特值体系法-两项特值与三项特值;-要素列表法plus-特殊套路-所有圆半径,球半径,均设为需要通过勾股定理求解;即要确定两个要素,需要两个关系;
-C-算术-绝对值-绝对值和-绝对值三角不等式-第一步:记住公式,绝对值差,和差绝对值,绝对值和。第二步:记住口诀:取等条件:中间相加取等号,左异右同零取到;中间相减取等号,上面符号方向调(其中,座椅油桶,左异右同是ab的正负号相同与否)
19.设a,b为实数,则能确定 ∣ a ∣ + ∣ b ∣ |a|+|b| ∣a∣+∣b∣的值。
(1)已知 ∣ a + b ∣ |a+b| ∣a+b∣的值。
(2)已知 ∣ a − b ∣ |a -b| ∣a−b∣的值。



真题(2021-24)-C-一个等号+一个不等号,一个定性+一个定量,选C(定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意));
-代数-数列-等比数列-数列判定
24.已知数列{a},则数列{a}为等比数列。
(1) a n a n + 1 > 0 a_na_{n+1}>0 anan+1>0。
(2) a n + 1 2 − 2 a n 2 − a n a n + 1 = 0 a^2_{n+1}-2a^2_n-a_na_{n+1}=0 an+12−2an2−anan+1=0。


2020
真题(2020-17)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
-几何-解析几何-位置-线圆位置-相切-圆心点到直线距离公式
17、曲线 上的点到 x 2 + y 2 = 2 x + 2 y x^2+y^2=2x+2y x2+y2=2x+2y上的点到 a x + b y + 2 = 0 ax+by+\sqrt2=0 ax+by+2=0的距离最小值大于 1。
(1) a 2 + b 2 = 1 a^2+b^2=1 a2+b2=1
(2) a > 0 , b > 0 a>0,b>0 a>0,b>0


真题(2020-18)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
-数据分析-数据描述-平均值与方差
18、若a, b, c 是实数,则能确定a, b, c 的最大值。
(1)已知a, b, c 的平均值。
(2)已知a, b, c 的最小值。


真题(2020-19)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
-数据分析-概率-已知元素的数量求概率⟹ 古典概型⟹ 两个排列组合相除计算概率或穷举法⟹ 分母有顺序要求是A运算,无顺序是C运算,分子数量少用穷举,数量多用C运算⟹ 袋中取球模型⟹ 正难则反⟹ 转为一次取球模型⟹ 设口袋中有a个白球,b个黑球,一次取出若干个球,则恰好取了 m ( m ≤ a ) m (m≤a) m(m≤a)个白球, n ( n ≤ b ) n(n≤b) n(n≤b)个黑球的概率是 P = C a m ⋅ C b n C a + b m + n P=\frac{C_a^m·C_b^n}{C_{a+b}^{m+n}} P=Ca+bm+nCam⋅Cbn。翻译“≥≤”-准确率90%-D:题干或选项可以翻译成≥或≤的,选D
19、甲、乙两种品牌手机共有 20 部,从中任选 2 部,则恰有 1 部甲品牌手机的概率大于 1 2 1\over2 21。
(1)甲手机不少于 8 部
(2)乙手机大于 7 部


2019
真题(2019-16)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
16、甲、乙、丙三人各自拥有不超过 10 本图书,甲再购入 2 本图书后,他们拥有的图书量构成等比数列,则能确定甲拥有图书的数量。
(1) 已知乙拥有的图书数量。
(2) 已知丙拥有的图书数量。


真题(2019-19)-C-两选项出现取值范围,判断是否有交集⇒有交集选C⇒无交集选A
19、能确定小明年龄。
(1)小明年龄是完全平方数。
(2)20年后小明年龄是完全平方数。


真题(2019-23)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
-数据分析-数据描述-平均值
23、某校理学院五个系每年录取人数如下表:
| 系数 | 数学系 | 物理系 | 化学系 | 生物系 | 地学系 |
|---|---|---|---|---|---|
| 录取人数 | 60 | 120 | 90 | 60 | 30 |
今年与去年相比,物理系平均分没交,则理学院录取平均分升高了。
(1) 数学系录取平均分升高了 3 分,生物系录取平均分降低了 2 分
(2) 化学系录取平均分升高了 1 分,地学系录取平均分降低了 4 分


2018
真题(2018-22)-C-选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D
-几何-解析几何-线性规划
22.已知点 P ( m , 0 ) P(m,0) P(m,0), A ( 1 , 3 ) A(1,3) A(1,3), B ( 2 , 1 ) , B(2,1), B(2,1),点 ( x , y ) (x,y) (x,y)在三角形PAB 上,则 x − y x- y x−y的最小值与最大值分别为-2和1。
(1) m ≤ 1 m ≤ 1 m≤1
(2) m ≥ − 2 m ≥ -2 m≥−2





2017
真题(2017-18)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
-应用题-路程
18.某人从 A 地出发,先乘时速为 220 千米的动车,后转乘时速为 100 千米的汽车到达 B 地,则 A,B 两地的距离为 960 千米。
(1)乘动车的时间与乘汽车的时间相等
(2)乘动车的时间与乘汽车的时间之和为 6 小时


真题(2017-23)-C-选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D
-数据分析-概率-已知各对象的概率求概率⟹ n重伯努利概型⟹ 用乘法或加法计算概率
23.某人参加资格考试,有 A 类和 B 类选择,A 类的合格标准是抽 3 道题至少会做 2 道,B 类的合格标准是抽 2 道题须都会做,则此人参加 A 类合格的机会大。
(1)此人 A 类题中有 60%会做。
(2)此人 B 类题中有 80%会做。


真题(2017-24)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
-应用题-整数不定方程
24.某机构向 12 位教师征题,共征集到 5 种题型的试题 52 道,则能确定供题教师的人数。
(1)每位供题教师提供题数相同
(2)每位供题教师提供的题型不超过 2 种


2016
真题(2016-17)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
-几何-平面几何-求面积-设未知数
17.如图 6,正方形 ABCD 由四个相同的长方形和一个小正形拼成,则能确定小正方形的面积。
(1)已知正方形 ABCD 的面积。
(2)已知长方形的长宽之比。
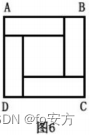

真题(2016-19)-C-特值法-两变量不等关系中的特值法
19.设 x , y x,y x,y是实数,则 x ≤ 6 , y ≤ 4 x≤6, y≤4 x≤6,y≤4。
(1) x ≤ y + 2 x≤y+2 x≤y+2
(2) 2 y ≤ x + 2 2y≤x+2 2y≤x+2


真题(2016-22)-C-定性+定量,选C-定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意)
几何-图像的判断
22.已知M是一个平面有限点集,则平面上存在到M中各点距离相等的点。
(1)M中只有三个点。
(2)M中的任意三点都不共线。

2015
真题(2015-22)-C
-应用题-整数不定方程
22.几个朋友外出游玩,购买了一些瓶装水,则能确定购买的瓶装水数量
(1)若每人分3 瓶,则剩余30 瓶
(2)若每人分10 瓶,则只有一人不够


真题(2015-24)-C-一个等号+一个不等号,一个定性+一个定量,选C(定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意));-C-整体规律+局部特例:大规律在前,局部特例在后,且整体规律不能代表局部特例,选C;-不同量选项秒杀-准确率90%-C:一个等号一个不等号(如a>0)或者一个定量一个定性(a为正数),选C;-C-几何-立体几何-圆柱体
- 底面半径为r ,高为h 的圆柱体表面积记为 S 1 S_1 S1,半径为 R 球体表面积记为 S 2 S_2 S2,则 S 1 ≤ S 2 S_1≤S_2 S1≤S2
(1) R ≥ R≥ R≥ r + h 2 {r+h}\over2 2r+h
(2) R ≤ R≤ R≤ r + 2 h 3 {r+2h}\over3 3r+2h


真题(2015-25)-C-一个等号+一个不等号,一个定性+一个定量,选C(定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意));-C选项蒙猜-整体规律+局部特例:整体规律+局部特例:大规律在前,局部特例在后,且整体规律不能代表局部特例,选C;
25.已知 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3为实数, x x x 为 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3的平均值,则 ∣ x k − x ∣ ≤ 1 , k = 1 , 2 , 3 |x_k-x|≤1,k=1,2,3 ∣xk−x∣≤1,k=1,2,3
(1) ∣ x k ∣ ≤ 1 , k = 1 , 2 , 3 |x_k|≤1,k=1,2,3 ∣xk∣≤1,k=1,2,3
(2) x 1 = 0 x_1=0 x1=0

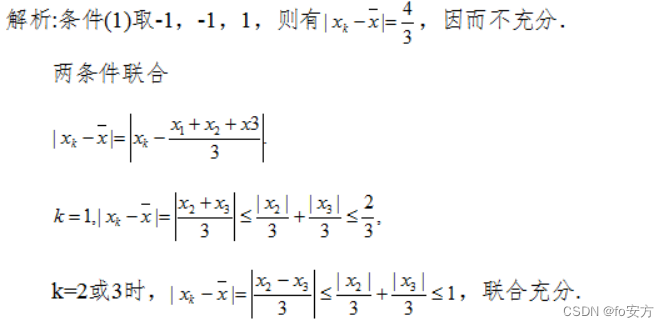


2014
真题(2014-18)-C-一个等号+一个不等号,一个定性+一个定量,选C(定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意));
-数列-等差数列&等比数列-既是等差数列又是等比数列的数列是非零的常数列
18.甲、乙、丙三人的年龄相同
(1)甲、乙、丙的年龄成等差数列
(2)甲、乙、丙的年龄成等比数列


真题(2014-22)-C-单一条件信息不完全,首选C;-要素列表法与维度思维;
-C-函数-一元二次函数-顶点坐标: ( − b 2 a , 4 a c − b 2 4 a ) (-\frac{b}{2a},\frac{4ac-b^2}{4a}) (−2ab,4a4ac−b2);
22.已知二次函数为 f ( x ) = a x 2 + b x + c f(x)=ax^2+bx+c f(x)=ax2+bx+c ,则能确定 a , b , c a, b, c a,b,c的值。
(1)曲线 y = f ( x ) y = f (x) y=f(x)过点 ( 0 , 0 ) (0, 0) (0,0)和点 ( 1 , 1 ) (1,1) (1,1)。
(2)曲线 y = f ( x ) y = f (x) y=f(x)与直线 y = a + b y = a + b y=a+b相切。


真题(2014-23)-C-一个等号+一个不等号,一个定性+一个定量,选C(定性+定量常为:①属性描述+等式;②不等式+等式;③属性描述+另一个(任意));-C-比较类问题要联合,首选C;
-数据分析-概率-已知元素的数量求概率⟹ 古典概型⟹ 两个排列组合相除计算概率或穷举法⟹ 分母有顺序要求是A运算,无顺序是C运算,分子数量少用穷举,数量多用C运算⟹ 袋中取球模型⟹ 正难则反⟹ 转为一次取球模型⟹ 设口袋中有a个白球,b个黑球,一次取出若干个球,则恰好取了 m ( m ≤ a ) m (m≤a) m(m≤a)个白球, n ( n ≤ b ) n(n≤b) n(n≤b)个黑球的概率是 P = C a m ⋅ C b n C a + b m + n P=\frac{C_a^m·C_b^n}{C_{a+b}^{m+n}} P=Ca+bm+nCam⋅Cbn;
23.已知袋中装有红、黑、白三种颜色的球若干个,则红球数量最多。
(1)随机取出的一球是白球的概率为 2 5 \frac{2}{5} 52
(2)随机取出的两球中至少有一个黑球的概率小于 1 5 \frac{1}{5} 51
秒杀:红>黑,且红>白


真题(2014-24)-C-本身条件差得远,但大前提限制为整数/自然数,导致可以充分;
-C-数据描述-平均值&方差
24.已知m={ a , b , c , d , e a,b,c,d,e a,b,c,d,e}是一个整数集合,则能确定集合m。
(1) a, b, c, d , e 的平均值为 10。
(2) a, b, c, d , e 的方差为 2。
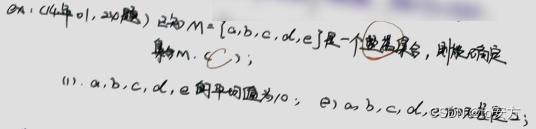


2013
真题(2013-21)-C-单一条件信息不完全,选C;-C-必联立选项秒杀-准确率75%-C:条件1与条件2必须联立,选C。(25%选E);-C-算术-绝对值-绝对值三角不等式
21.已知a,b 为实数,则 ∣ a ∣ ≤ 1 , ∣ b ∣ ≤ 1 |a|≤1,|b|≤1 ∣a∣≤1,∣b∣≤1。
(1) ∣ a + b ∣ ≤ 1 |a+b|≤1 ∣a+b∣≤1
(2) ∣ a − b ∣ ≤ 1 |a-b|≤1 ∣a−b∣≤1
方法二:举反例,往大值取(满足条件,不满足题干)。如(1)a=10,b=-10,不充分;(2)a=10,b=10,不充分。考试时不要证明联立情况,充分必要题秒杀:最难选择C或E,75%选C,25%选E。


真题(2013-22)-C-单一条件信息不完全,选C;
-C-代数-分式-齐次分式;
22.设 x , y , z x, y, z x,y,z为非零实数,则 2 x + 3 y − 4 z − x + y − 2 z = 1 \frac{2x+3y-4z}{-x+y-2z}=1 −x+y−2z2x+3y−4z=1。
(1) 3 x − 2 y = 0 3x-2y=0 3x−2y=0
(2) 2 y − z = 0 2y-z=0 2y−z=0

这篇关于管理类联考——数学——真题篇——按题型分类——充分性判断题——蒙猜C的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









