本文主要是介绍储备池计算(Reservoir Computing) ~ 前沿案例更新中,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
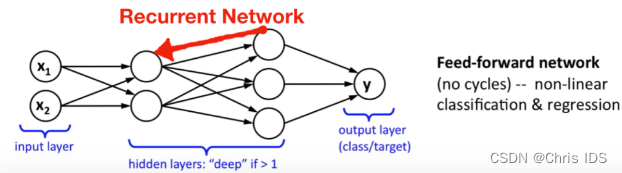
Reservoir Computing, 也叫Echo state network(回声网络), 被视为是神经网络(Neural Network)的一种拓展框架。
目录
一、ESN
Echo state networks (ESN)
ESN的思想
ESN的结构和训练步骤
比较官方的解释
二、储备池 计算 三个组成部分
Reservoir有以下三个关键特性
三、运行过程
3.1 训练
3.2 测试
四、示例
4.1 模拟
4.2 预测
五、一些很牛的栗子
5.1 北京大学黄如院士-杨玉超教授团队在深度储备池计算硬件研究中取得进展
5.2 哈工大(深圳)赵毅教授团队:储备池计算模型的更紧致泛化上限
一、ESN
Echo state networks (ESN)
Echo state networks provide an architecture and supervised learning principle for recurrent neural networks (RNNs). The main idea is (i) to drive a random, large, fixed recurrent neural network with the input signal, thereby inducing in each neuron within this "reservoir" network a nonlinear response signal, and (ii) combine a desired output signal by a trainable linear combination of all of these response signals.
给定一段信号:u(0), u(1), ... , u(Nt-1);
目标值:v(1), v(2), ... , v(Nt)
学习黑箱模型M,可得预测v(Nt+1), v(Nt+2), ...
ESN的思想
使用大规模随机稀疏网络(储备池)作为信息处理媒介,将输入信号从低维的输入空间映射到高维的状态空间,在高维的状态空间采用线性回归方法对网络的部分连接权进行训练,而其他连接权随机产生,并在网络训练过程中保持不变。这种思想在Steil关于传统递归神经网络的经典算法(Atiya-Parlos)的研究中也得到了验证:递归神经网络输出连接权改变迅速,而内部连接权则以高度耦合的方式缓慢改变。也就是说,如果递归神经网络内部连接权选择合适,在对网络进行训练时可以忽略内部连接权的改变。
ESN的结构和训练步骤
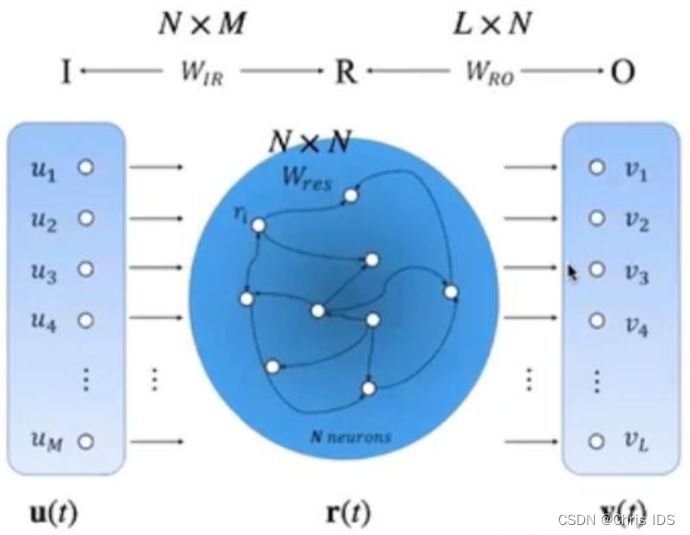
结构如上图:r(t)为“储备池”,它有以下特点:
(1)包含数目更多的神经元;
(2)神经元之间的连接关系随机产生;
(3)神经元之间的连接具有稀疏性。
上面的两个参数矩阵![]() 都是事先给定的数值,在训练的过程中只需要计算
都是事先给定的数值,在训练的过程中只需要计算即可。
整个计算过程如下所示:
(1)从输入到储备池(reservoir)的运算:;
(2)储备池中r ( t ) 的更新:;
(3)从储备池到输出:;
(4)损失函数:;
(5)使损失函数最小化 ……
比较官方的解释
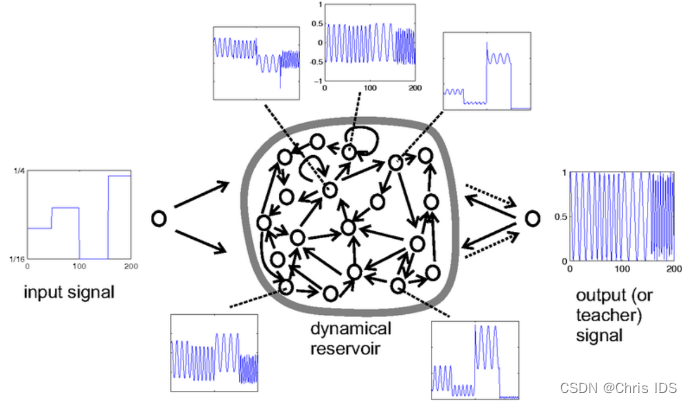
- Step 1: Provide a random RNN. (i) Create a random dynamical reservoir RNN, using any neuron model (in the frequency generator demo example, non-spiking leaky integrator neurons were used). The reservoir size N is task-dependent. In the frequency generator demo task, N=200 was used. (ii) Attach input units to the reservoir by creating random all-to-all connections. (iii) Create output units. If the task requires output feedback (the frequency-generator task does), install randomly generated output-to-reservoir connections (all-to-all). If the task does not require output feedback, do not create any connections to/from the output units in this step.
- Step 2: Harvest reservoir states. Drive the dynamical reservoir with the training data D for times n=1,…,nmax . In the demo example, where there are output-to-reservoir feedback connections, this means to write both the input u(n) into the input unit and the teacher output y(n) into the output unit ("teacher forcing"). In tasks without output feedback, the reservoir is driven by the input u(n) only. This results in a sequence x(n) of N-dimensional reservoir states. Each component signal x(n) is a nonlinear transform of the driving input. In the demo, each x(n) is an individual mixture of both the slow step input signal and the fast output sinewave (see the five exemplary neuron state plots in Figure 1).
- Step 3: Compute output weights. Compute the output weights as the linear regression weights of the teacher outputs y(n) on the reservoir states x(n) . Use these weights to create reservoir-to-output connections (dotted arrows in Figure 1). The training is now completed and the ESN ready for use. Figure 2 shows the output signal obtained when the trained ESN was driven with the slow step input shown in the same figure.
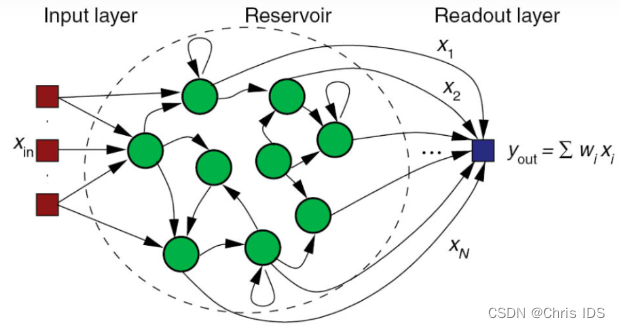
二、储备池 计算 三个组成部分
- 输入层(input layer): 可以由一个或多个node组成, 属于前馈神经网络(feed-forward Neural network)的一种.
- 中间层(middle layer): 由多个node组成, 属于递归神经网络(recurrent Neural network)的一种.
- 输出层(output layer): 带有权重的加法器(weighted summer).
前馈神经网络与递归神经网络的差别:
前者只允许信号从输入层向前传到输出层,信号的传递是单向的,它也不存在任何的回路,也就是说任何一层的输出都无法影响这层本身的数据,一般用于模式识别;后者通过引入循环的方法允许信号双向传递。
Reservoir有以下三个关键特性
- 通常储备池有很多节点,且节点的连接是稀疏的,故矩阵是稀疏矩阵
- 由于节点之间会形成很多循环,故储备池中的nodes形成的是递归神经网络
- 各个节点会在学习阶段使用一种高效递归的架构使节点的权重不断更新
Attention:储备池计算的关键特点在于:中间层的reservoir矩阵是随机生成的且生成后就保持不变,真正需要训练的只有输出层,这也使它比传统的方法快很多。
Reservoir Computing的概念,简单来说就是给一个随机连接的Spiking Neural Network(称为reservoir)一些输入,然后用现有的机器学习的方法来学习这个Network对于特定的输入的pattern,从而达到pattern recognition的目的。可以做一个类比,如果把SNN等同于大脑的circuit的话,那么Reservoir Computing就是从大脑circuit里接出几个输出,然后判断这些连接输出地神经元都以怎样的pattern活动并归类,从而判别输入端接受到了怎样的信息(这点有点像利用EEG做Brain Computer Interface的方法)。当然Reservoir的模型可以不仅限于SNN,node的模型也可以各种各样,包括之前提到Izhikevich的Polychronization,就有人利用其作为Reservoir做了一些模式识别方面的研究。
Attention~ 以下是对知乎QA中有理的解释的摘录,大家也可以发表自己的看法
RC的好处是特征提取网络,即Reservoir ,是随机生成并在训练和预测阶段是固定的,只有readout部分是要学的,trainable参数相对RNN要少,训练很快。
RC的缺点主要在于表达能力,数据量大的话精度受限。RC应该更适用于中小数据量的问题,比如生物医疗中的数据,但对于计算机视觉,自然语言处理等数据量大、标注丰富的领域,RC不如RNN表达能力好,因此性能也会打折扣。
三、运行过程
from Reservoir Computing 简介
下面提出一种reservoir computing的示例,该reservoir的输入层有M个节点,中间层有N个节点,输出层有P个节点,reservoir dynamics被定义为:
其中各变量意义如下:
- α: leakage rate,主要用来控制reservoir中各节点权重更新的速度
- r: reservoir state vector,记录了reservoir中每个节点的权重信息
- A: reservoir的权重邻接矩阵(weighted adjacency matrix),通常是一个稀疏矩阵,这里用Erdős–Rényi来生成
- Win: N行M列的矩阵,主要是用来将M维的输入信号转换为reservoir可接受的形式
- u(t): 输入信号,维度为M
- ξ: bias,即偏置
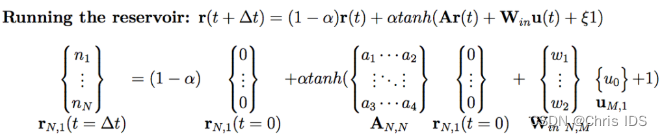
3.1 训练
前期主要分为两个阶段,初始阶段(Initial period)和训练阶段(Training period)。在初始阶段,一般认为所有信号都是已知的,此时无需记录reservoir中节点的状态。当初始阶段结束训练阶段开始时,需要将每一次计算得到的reservoir状态记录到一个矩阵中。

收集到这些状态以后,就可以训练输出层了,这里使用ridge regression来训练。
3.2 测试
训练得到Wout之后,就可以使用公式来测试reservoir了。

四、示例
该reservoir有两种用法,模拟信号与预测信号。
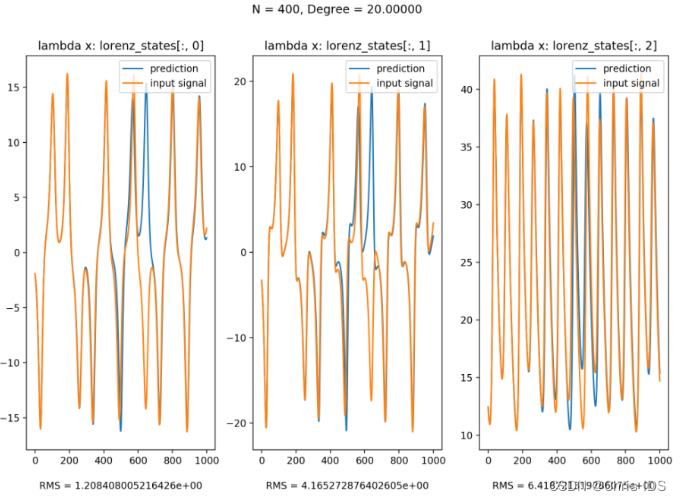
4.1 模拟
将Lorenz System的三个信号作为input signal,并在训练完成之后移除该signal,而将该reservoir产生的值作为input signal再输入reservoir。从图中可以看到,该reservoir良好地模拟了Lorenz System。
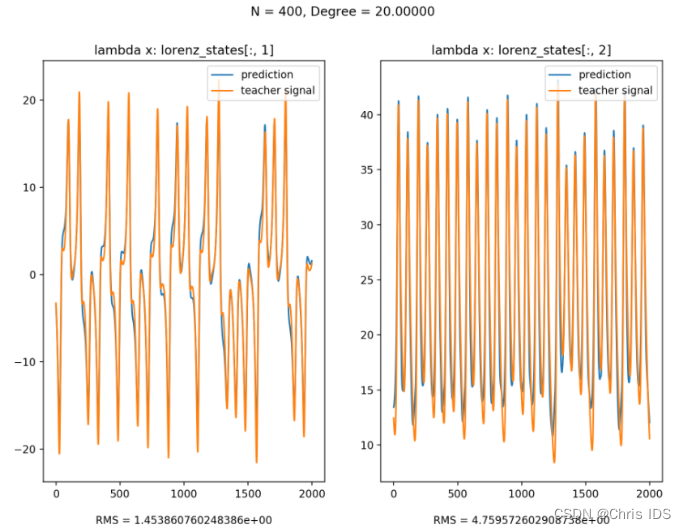
4.2 预测
举例:以x作为input signal, y & z作为teacher signal来训练,训练后便可以使用x来预测y & z:
五、一些很牛的栗子
5.1 北京大学黄如院士-杨玉超教授团队在深度储备池计算硬件研究中取得进展
储备池计算(Reservoir Computing)是一种低训练代价、低硬件开销的循环神经网络(RNN),在时序信息处理方面具有广泛的应用,例如波形分类、语音识别、时间序列预测等。储备池计算系统由神经元循环连接的储备池和输出层两部分组成,其中仅有输出层需要训练,从而显著降低了训练代价,而系统中的储备池可以由具有短时程特性的非线性器件来实现。当前国际上针对储备池计算系统的研究主要集中在探索使用不同类型的非线性器件(如忆阻器、自旋扭矩振荡器、纳米线网络、半导体光学放大器等)来构建单层储备池,但储备池状态数、记忆容量、复杂动力学特性等的局限从根本上制约了系统本身信息处理能力的提升。
针对这一关键问题,北京大学集成电路学院黄如院士-杨玉超教授课题组首次采用可级联短时程非线性单元构建了深度储备池(deep reservoir)计算硬件,通过储备池层数的增加实现了层次化的信息处理能力、更丰富的储备池状态数、更大的记忆容量以及更复杂的动力学特性。该工作在构建深度储备池计算硬件系统、实现层次化的时序信息处理方面迈出了重要一步。
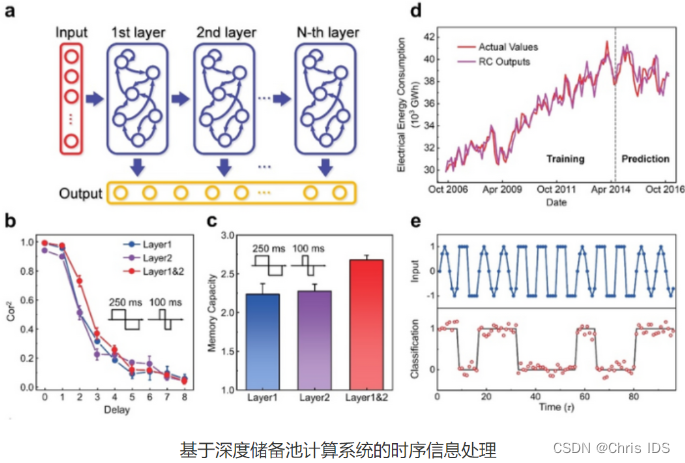
在技术路线上,北京大学集成电路学院研究团队研制了可级联的单层储备池硬件,通过将动态忆阻晶体管与平面器件进行串联分压,实现了电压输入、电压输出的短时程非线性单元。由于输入和输出为相同的物理量,解决了通常情况下电压输入、电流输出器件难以直接级联的问题,为构建深度储备池计算硬件奠定了器件基础。基于该类短时程非线性单元,他们进一步制备了深度储备池硬件系统,并结合分时复用的虚拟节点方法,获得了丰富的储备池状态。实验研究结果表明,相比同等规模的单层储备池计算系统,该工作所构建的深度储备池计算硬件具有更大的记忆容量、更丰富的储备池状态数、层次化的信息处理能力,并在波形分类、电能消耗预测等任务中展示了优异的性能,证明了深度储备池计算系统在时序信息处理任务中的潜力。
5.2 哈工大(深圳)赵毅教授团队:储备池计算模型的更紧致泛化上限
储备池计算模型(Reservoir Computing, RC)作为当前热门的轻量化深度学习模型之一,成功应用到真实复杂系统的建模分析中。这些实际应用彰显了RC模型良好的泛化性。而如何理解RC模型的泛化性尤其是其泛化能力上限则是至关重要的。
来自哈尔滨工业大学(深圳)赵毅教授团队为RC模型提供了一种泛化误差分析理论框架。该框架给出RC模型泛化误差理论上界,基于此更准确地量化RC模型的泛化能力。 在此基础上,推导出一般RC模型在时序预测任务中泛化误差所满足的理论上界。如下图所示,与现有的方法对比发现,他们为RC模型推导出一种更紧的泛化误差上界。该泛化误差上界也刻画出RC模型实际经验泛化误差与模型超参数之间的关联关系。
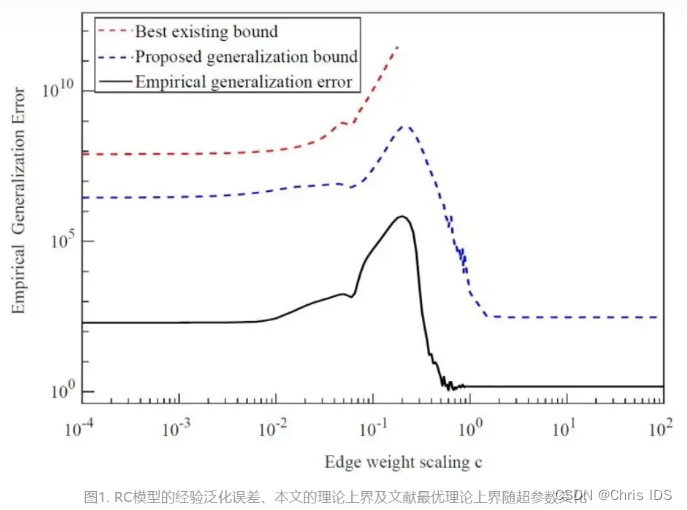
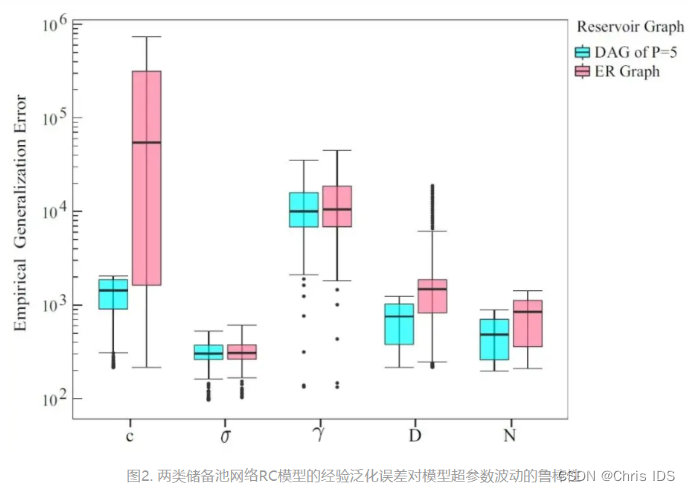
在明确RC模型泛化上限的基础上,作者关注网络结构等具体构成对提出的理论泛化能力的影响作用。 他们以ER无向储备池网络和有向无环储备池网络为例,推导出各自对应RC模型的泛化误差理论上界。通过比较发现,基于有向无环储备池网络的RC模型在泛化性能方面具有明显的优势。相比于ER无向储备池网络,有向无环储备池网络的RC模型的泛化性能对模型超参数波动呈现更好的鲁棒性(见图2所示),从而降低了RC模型超参数优化选择的难度。因此,作者提到“有向无环网络可作为储备池网络在实际应用中的默认选择。”
这篇关于储备池计算(Reservoir Computing) ~ 前沿案例更新中的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!