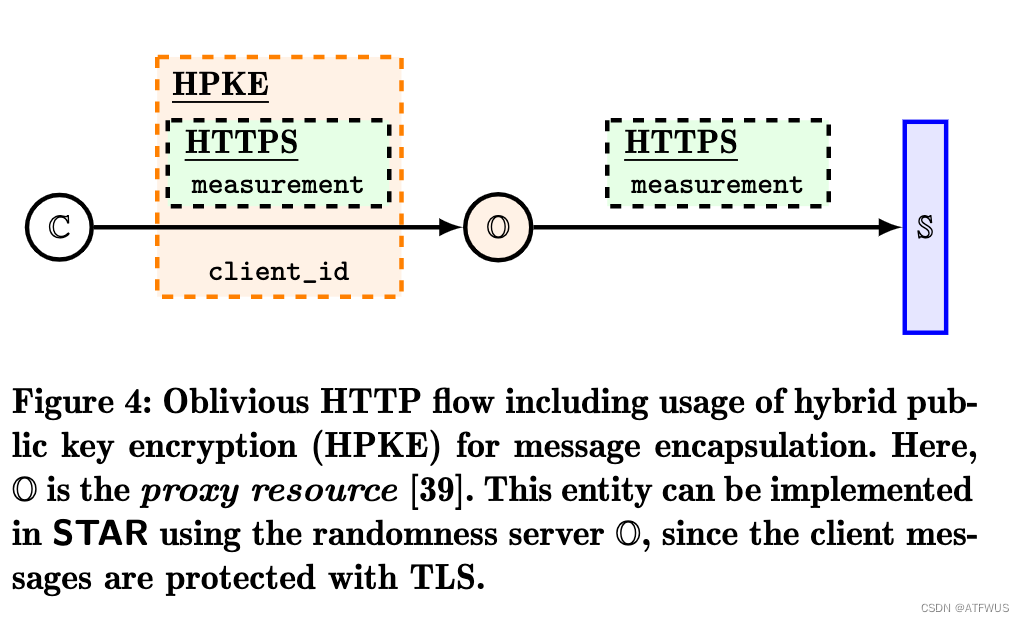
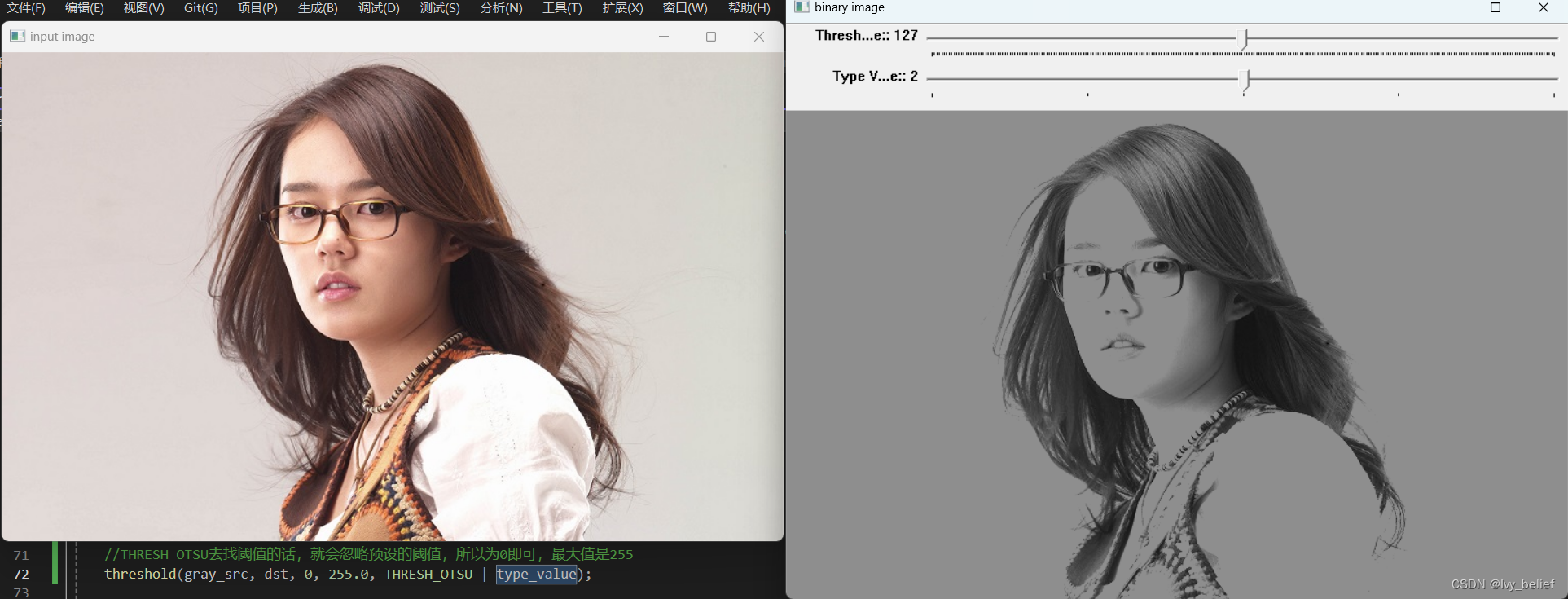
本文主要是介绍threshold,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
threshold
Логистическая регрессия — полезный классический инструмент для решения задачи регрессии и классификации. ROC-анализ — аппарат для анализа качества моделей. Оба алгоритма активно используются для построения моделей в медицине и проведения клинических исследований." />
<link rel="stylesheet" media="all" href="/sites/default/files/css/css_eMuzBBIj5x6opuBtwfyKEP6hjgSfcNbAq9UuiNq_P6Q.css" />
<script type="application/json" data-drupal-selector="drupal-settings-json">{"path":{"baseUrl":"\/","scriptPath":null,"pathPrefix":"","currentPath":"node\/437","currentPathIsAdmin":false,"isFront":false,"currentLanguage":"ru"},"pluralDelimiter":"\u0003","suppressDeprecationErrors":true,"ajaxPageState":{"libraries":"ajax_loader\/ajax_loader.throbber,az_comments\/az_comments.build,az_subform\/az_subform_res,codesnippet\/codesnippet.highlightjs,codesnippet\/codesnippet.style.atelier-forest.light,core\/html5shiv,lg_jsadv\/lg_jsadv.resources,lomru\/additional-fonts-1,lomru\/blogpost,lomru\/global-styling,lomru\/katex,lomru\/photoswipe,lomru\/plyr-356,lomru\/slick-slider-build,lomru\/special-line,lomru\/tooltipster-build,system\/base,views\/views.module","theme":"lomru","theme_token":null},"ajaxTrustedUrl":[],"ajaxLoader":{"markup":"\u003Cdiv class=\u0022ajax-throbber sk-wave\u0022\u003E\n \u003Cdiv class=\u0022sk-rect sk-rect1\u0022\u003E\u003C\/div\u003E\n \u003Cdiv class=\u0022sk-rect sk-rect2\u0022\u003E\u003C\/div\u003E\n \u003Cdiv class=\u0022sk-rect sk-rect3\u0022\u003E\u003C\/div\u003E\n \u003Cdiv class=\u0022sk-rect sk-rect4\u0022\u003E\u003C\/div\u003E\n \u003Cdiv class=\u0022sk-rect sk-rect5\u0022\u003E\u003C\/div\u003E\n \u003C\/div\u003E","hideAjaxMessage":false,"alwaysFullscreen":false,"throbberPosition":"body"},"lomru":{"project_env":"production","project_host":"https:\/\/loginom.ru\/"},"user":{"uid":0,"permissionsHash":"fa72860b8dd8a2e193e24f073a696eeecd53d85942fcc3648fbea14bedf1d186"}}</script>
<link href="https://fonts.googleapis.com/css?family=Source+Sans+Pro:400,600,700,900&subset=cyrillic" rel="stylesheet"><link rel="apple-touch-icon" sizes="180x180" href="/themes/custom/lomru/images/favicon/apple-touch-icon.png"><link rel="icon" type="image/png" href="/themes/custom/lomru/images/favicon/favicon-32x32.png?v=2" sizes="32x32"><link rel="icon" type="image/png" href="/themes/custom/lomru/images/favicon/favicon-16x16.png?v=2" sizes="16x16"><link rel="manifest" href="/themes/custom/lomru/images/favicon/manifest.json"><link rel="mask-icon" href="/themes/custom/lomru/images/favicon/safari-pinned-tab.svg" color="#5bbad5"><meta name="theme-color" content="#ffffff">

Логистическая регрессия и ROC-анализ — математический аппарат

Математический аппарат и назначение бинарной логистической регрессии — популярного инструмента для решения задач регрессии и классификации. ROC-анализ тесно связан с бинарной логистической регрессией и применяется для оценки качества моделей: позволяет выбрать аналитику модель с наилучшей прогностической силой, проанализировать чувствительность и специфичность моделей, подобрать порог отсечения.
Введение
Логистическая регрессия — полезный классический инструмент для решения задачи регрессии и классификации. ROC-анализ — аппарат для анализа качества моделей. Оба алгоритма активно используются для построения моделей в медицине и проведения клинических исследований.
Логистическая регрессия получила распространение в скоринге для расчета рейтинга заемщиков и управления кредитными рисками. Поэтому, несмотря на свое «происхождение» из статистики, логистическую регрессию и ROC-анализ почти всегда можно увидеть в наборе Data Mining алгоритмов.
Логистическая регрессия
Логистическая регрессия — это разновидность множественной регрессии, общее назначение которой состоит в анализе связи между несколькими независимыми переменными (называемыми также регрессорами или предикторами) и зависимой переменной. Бинарная логистическая регрессия применяется в случае, когда зависимая переменная является бинарной (т.е. может принимать только два значения). С помощью логистической регрессии можно оценивать вероятность того, что событие наступит для конкретного испытуемого (больной/здоровый, возврат кредита/дефолт и т.д.).
Все регрессионные модели могут быть записаны в виде формулы:
y = F (x_1,\, x_2, \,\dots, \, x_n)
В множественной линейной регрессии предполагается, что зависимая переменная является линейной функцией независимых переменных, т.е.:
y = a\,+\,b_1\,x_1\,+\,b_2\,x_2\,+\,\dots\,+\,b_n\,x_n
Можно ли ее использовать для задачи оценки вероятности исхода события? Да, можно, вычислив стандартные коэффициенты регрессии. Например, если рассматривается исход по займу, задается переменная y со значениями 1 и 0, где 1 означает, что соответствующий заемщик расплатился по кредиту, а 0, что имел место дефолт.
Однако здесь возникает проблема: множественная регрессия не «знает», что переменная отклика бинарна по своей природе. Это неизбежно приведет к модели с предсказываемыми значениями большими 1 и меньшими 0. Но такие значения вообще не допустимы для первоначальной задачи. Таким образом, множественная регрессия просто игнорирует ограничения на диапазон значений для y.
Для решения проблемы задача регрессии может быть сформулирована иначе: вместо предсказания бинарной переменной, мы предсказываем непрерывную переменную со значениями на отрезке [0,1] при любых значениях независимых переменных. Это достигается применением следующего регрессионного уравнения (логит-преобразование):
P = \frac{1}{1+\,e^{-y}}
где P — вероятность того, что произойдет интересующее событие e — основание натуральных логарифмов 2,71…; y — стандартное уравнение регрессии.
Зависимость, связывающая вероятность события и величину y, показана на следующем графике (рис. 1):
Рис. 1 — Логистическая кривая
Поясним необходимость преобразования. Предположим, что мы рассуждаем о нашей зависимой переменной в терминах основной вероятности P, лежащей между 0 и 1. Тогда преобразуем эту вероятность P:
P' = \log_e \Bigl(\frac{P}{1-P}\Bigr)
Это преобразование обычно называют логистическим или логит-преобразованием. Теоретически P' может принимать любое значение. Поскольку логистическое преобразование решает проблему об ограничении на 0-1 границы для первоначальной зависимой переменной (вероятности), то эти преобразованные значения можно использовать в обычном линейном регрессионном уравнении. А именно, если произвести логистическое преобразование обеих частей описанного выше уравнения, мы получим стандартную модель линейной регрессии.
Существует несколько способов нахождения коэффициентов логистической регрессии. На практике часто используют метод максимального правдоподобия. Он применяется в статистике для получения оценок параметров генеральной совокупности по данным выборки. Основу метода составляет функция правдоподобия (likehood function), выражающая плотность вероятности (вероятность) совместного появления результатов выборки
L\,(Y_1,\,Y_2,\,\dots,\,Y_k;\,\theta) = p\,(Y_1;\, \theta)\cdot\dots\cdotp\,p\,(Y_k;\,\theta)
Согласно методу максимального правдоподобия в качестве оценки неизвестного параметра принимается такое значение \theta=\theta(Y_1,…,Y_k), которое максимизирует функцию L.
Нахождение оценки упрощается, если максимизировать не саму функцию L, а натуральный логарифм ln(L), поскольку максимум обеих функций достигается при одном и том же значении \theta:
L\,*\,(Y;\,\theta) = \ln\,(L\,(Y;\,\theta)\,) \rightarrow \max
В случае бинарной независимой переменной, которую мы имеем в логистической регрессии, выкладки можно продолжить следующим образом. Обозначим через P_i вероятность появления единицы: P_i=Prob(Y_i=1). Эта вероятность будет зависеть от X_iW, где X_i — строка матрицы регрессоров, W — вектор коэффициентов регрессии:
P_i = F\,(X_i W),\, F(z) = \frac{1}{1+\,e^{-z}}
Логарифмическая функция правдоподобия равна:
L^* = \sum_{i \epsilon\ I_1}ln{P_i(W)} + \sum_{i \epsilon\ I_0}ln{(1-P_i(W))} = \sum_{i=1}^{k} [Y_i \ln {P_i (W)}+(1-Y_i)\ln {(1 - P_i(W))}]
где I_0, I_1— множества наблюдений, для которых Y_i=0 и Y_i=1 соответственно.
Можно показать, что градиент g и гессиан H функции правдоподобия равны:
g = \sum_i (Y_i\,-\,P_i)\,X_i
H=-\sum_i P_i\,(1\,-\,P_i)\,X_i^T\,X_i\,\leq 0
Гессиан всюду отрицательно определенный, поэтому логарифмическая функция правдоподобия всюду вогнута. Для поиска максимума можно использовать метод Ньютона, который здесь будет всегда сходиться (выполнено условие сходимости метода):
W_{t+1}\,=\,W_t\,-\,(H\,(W_t))^{-1}\,g_t(W_t)\,=\,W_t\,-\,\Delta W_t
Логистическую регрессию можно представить в виде однослойной нейронной сети с сигмоидальной функцией активации, веса которой есть коэффициенты логистической регрессии, а вес поляризации — константа регрессионного уравнения (рис. 2).
Рис. 2 — Представление логистической регрессии в виде нейронной сети
Однослойная нейронная сеть может успешно решить лишь задачу линейной сепарации. Поэтому возможности по моделированию нелинейных зависимостей у логистической регрессии отсутствуют. Однако для оценки качества модели логистической регрессии существует эффективный инструмент ROC-анализа, что является несомненным ее преимуществом.
Для расчета коэффициентов логистической регрессии можно применять любые градиентные методы: метод сопряженных градиентов, методы переменной метрики и другие.
ROC-анализ
ROC-кривая (Receiver Operator Characteristic) — кривая, которая наиболее часто используется для представления результатов бинарной классификации в машинном обучении. Название пришло из систем обработки сигналов. Поскольку классов два, один из них называется классом с положительными исходами, второй — с отрицательными исходами. ROC-кривая показывает зависимость количества верно классифицированных положительных примеров от количества неверно классифицированных отрицательных примеров.
В терминологии ROC-анализа первые называются истинно положительным, вторые — ложно отрицательным множеством. При этом предполагается, что у классификатора имеется некоторый параметр, варьируя который, мы будем получать то или иное разбиение на два класса. Этот параметр часто называют порогом, или точкой отсечения (cut-off value). В зависимости от него будут получаться различные величины ошибок I и II рода.
В логистической регрессии порог отсечения изменяется от 0 до 1 — это и есть расчетное значение уравнения регрессии. Будем называть его рейтингом.
Для понимания сути ошибок I и II рода рассмотрим четырехпольную таблицу сопряженности (confusion matrix), которая строится на основе результатов классификации моделью и фактической (объективной) принадлежностью примеров к классам.
| Модель | Фактически положительно | Фактически отрицательно |
|---|---|---|
| Положительно | TP | FP |
| Отрицательно | FN | TN |
- TP (True Positives) — верно классифицированные положительные примеры (так называемые истинно положительные случаи).
- TN (True Negatives) — верно классифицированные отрицательные примеры (истинно отрицательные случаи).
- FN (False Negatives) — положительные примеры, классифицированные как отрицательные (ошибка I рода). Это так называемый «ложный пропуск» — когда интересующее нас событие ошибочно не обнаруживается (ложно отрицательные примеры).
- FP (False Positives) — отрицательные примеры, классифицированные как положительные (ошибка II рода). Это ложное обнаружение, т.к. при отсутствии события ошибочно выносится решение о его присутствии (ложно положительные случаи).
Что является положительным событием, а что — отрицательным, зависит от конкретной задачи. Например, если мы прогнозируем вероятность наличия заболевания, то положительным исходом будет класс «Больной пациент», отрицательным — «Здоровый пациент». И наоборот, если мы хотим определить вероятность того, что человек здоров, то положительным исходом будет класс «Здоровый пациент», и так далее.
При анализе чаще оперируют не абсолютными показателями, а относительными — долями (rates), выраженными в процентах:
- Доля истинно положительных примеров (True Positives Rate): TPR = \frac{TP}{TP\,+\,FN}\,\cdot\,100 \,\%
- Доля ложно положительных примеров (False Positives Rate): FPR = \frac{FP}{TN\,+\,FP}\,\cdot\,100 \,\%
Введем еще два определения: чувствительность и специфичность модели. Ими определяется объективная ценность любого бинарного классификатора.
Чувствительность (Sensitivity) — это и есть доля истинно положительных случаев:
S_e = TPR = \frac{TP}{TP\,+\,FN}\,\cdot\,100 \,\%
Специфичность (Specificity) — доля истинно отрицательных случаев, которые были правильно идентифицированы моделью:
S_p = \frac{TN}{TN\,+\,FP}\,\cdot\,100 \,\%
Заметим, что FPR=100-Sp
Попытаемся разобраться в этих определениях.
Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (обнаруживает положительные примеры). Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (обнаруживает отрицательные примеры). Если рассуждать в терминах медицины — задачи диагностики заболевания, где модель классификации пациентов на больных и здоровых называется диагностическим тестом, то получится следующее:
- Чувствительный диагностический тест проявляется в гипердиагностике — максимальном предотвращении пропуска больных.
- Специфичный диагностический тест диагностирует только доподлинно больных. Это важно в случае, когда, например, лечение больного связано с серьезными побочными эффектами и гипердиагностика пациентов не желательна.
ROC-кривая получается следующим образом:
Для каждого значения порога отсечения, которое меняется от 0 до 1 с шагом d_x (например, 0,01) рассчитываются значения чувствительности Se и специфичности Sp. В качестве альтернативы порогом может являться каждое последующее значение примера в выборке.
Строится график зависимости: по оси Y откладывается чувствительность Se, по оси X — FPR=100-Sp — доля ложно положительных случаев.
Канонический алгоритм построения ROC-кривой
Входы: L — множество примеров f[i] — рейтинг, полученный моделью, или вероятность того, что i-й пример имеет положительный исход; min и max — минимальное и максимальное значения, возвращаемые f; d_x — шаг; P и N — количество положительных и отрицательных примеров соответственно.
- t=min
- повторять
- FP=TP=0
- для всех примеров i принадлежит L {
- если f[i]>=t тогда // этот пример находится за порогом
- если i положительный пример тогда
- { TP=TP+1 }
- иначе // это отрицательный пример
- { FP=FP+1 }
- }
- Se=TP/P*100
- point=FP/N // расчет (100 минус Sp)
- Добавить точку (point, Se) в ROC-кривую
- t=t+d_x
- пока (t>max)
В результате вырисовывается некоторая кривая (рис. 3).
Рис. 3 — ROC-кривая
График часто дополняют прямой y=x.
Заметим, что имеется более экономичный способ расчета точек ROC-кривой, чем тот, который приводился выше, т.к. его вычислительная сложность нелинейная и равна O(n^2): для каждого порога необходимо «пробегать» по записям и каждый раз рассчитывать TP и FP. Если же двигаться вниз по набору данных, отсортированному по убыванию выходного поля классификатора (рейтингу), то можно за один проход вычислить значения всех точек ROC-кривой, последовательно обновляя значения TP и FP.
Для идеального классификатора график ROC-кривой проходит через верхний левый угол, где доля истинно положительных случаев составляет 100% или 1,0 (идеальная чувствительность), а доля ложно положительных примеров равна нулю. Поэтому чем ближе кривая к верхнему левому углу, тем выше предсказательная способность модели. Наоборот, чем меньше изгиб кривой и чем ближе она расположена к диагональной прямой, тем менее эффективна модель. Диагональная линия соответствует «бесполезному» классификатору, т.е. полной неразличимости двух классов.
При визуальной оценке ROC-кривых расположение их относительно друг друга указывает на их сравнительную эффективность. Кривая, расположенная выше и левее, свидетельствует о большей предсказательной способности модели. Так, на рис. 4 две ROC-кривые совмещены на одном графике. Видно, что модель «A» лучше.
Рис. 4 — Сравнение ROC-кривых
Визуальное сравнение кривых ROC не всегда позволяет выявить наиболее эффективную модель. Своеобразным методом сравнения ROC-кривых является оценка площади под кривыми. Теоретически она изменяется от 0 до 1,0, но, поскольку модель всегда характеризуются кривой, расположенной выше положительной диагонали, то обычно говорят об изменениях от 0,5 («бесполезный» классификатор) до 1,0 («идеальная» модель).
Эта оценка может быть получена непосредственно вычислением площади под многогранником, ограниченным справа и снизу осями координат и слева вверху — экспериментально полученными точками (рис. 5). Численный показатель площади под кривой называется AUC (Area Under Curve). Вычислить его можно, например, с помощью численного метода трапеций:
AUC = \int f(x)\,dx = \sum_i \Bigl[ \frac{X_{i+1}\,+\,X_i}{2}\Bigr]\,\cdot \,(Y_{i+1}\,-\, Y_i)
Рис. 5 — Площадь под ROC-кривой
С большими допущениями можно считать, что чем больше показатель AUC, тем лучшей прогностической силой обладает модель. Однако следует знать, что:
- показатель AUC предназначен скорее для сравнительного анализа нескольких моделей;
- AUC не содержит никакой информации о чувствительности и специфичности модели.
В литературе иногда приводится следующая экспертная шкала для значений AUC, по которой можно судить о качестве модели:
| Интервал AUC | Качество модели |
|---|---|
| 0,9-1,0 | Отличное |
| 0,8-0,9 | Очень хорошее |
| 0,7-0,8 | Хорошее |
| 0,6-0,7 | Среднее |
| 0,5-0,6 | Неудовлетворительное |
Идеальная модель обладает 100% чувствительностью и специфичностью. Однако на практике добиться этого невозможно, более того, невозможно одновременно повысить и чувствительность, и специфичность модели. Компромисс находится с помощью порога отсечения, т.к. пороговое значение влияет на соотношение Se и Sp. Можно говорить о задаче нахождения оптимального порога отсечения (optimal cut-off value).
Порог отсечения нужен для того, чтобы применять модель на практике: относить новые примеры к одному из двух классов. Для определения оптимального порога нужно задать критерий его определения, т.к. в разных задачах присутствует своя оптимальная стратегия. Критериями выбора порога отсечения могут выступать:
- Требование минимальной величины чувствительности (специфичности) модели. Например, нужно обеспечить чувствительность теста не менее 80%. В этом случае оптимальным порогом будет максимальная специфичность (чувствительность), которая достигается при 80% (или значение, близкое к нему «справа» из-за дискретности ряда) чувствительности (специфичности).
- Требование максимальной суммарной чувствительности и специфичности модели, т.е. Cutt\underline{\,\,\,}off_o = \max_k (Se_k\,+\,Sp_k)
- Требование баланса между чувствительностью и специфичностью, т.е. когда Se \approx Sp: Cutt\underline{\,\,\,}off_o = \min_k \,\bigl |Se_k\,-\,Sp_k \bigr |
Второе значение порога обычно предлагается пользователю по умолчанию. В третьем случае порог есть точка пересечения двух кривых, когда по оси X откладывается порог отсечения, а по оси Y — чувствительность или специфичность модели (рис. 6).
Рис. 6 — «Точка баланса» между чувствительностью и специфичностью
Существуют и другие подходы, когда ошибкам I и II рода назначается вес, который интерпретируется как цена ошибок. Но здесь встает проблема определения этих весов, что само по себе является сложной, а часто не разрешимой задачей.
Литература
- Цыплаков А. А. Некоторые эконометрические методы. Метод максимального правдоподобия в эконометрии. Учебное пособие.
- Fawcett T. ROC Graphs: Notes and Practical Considerations for Researchers // 2004 Kluwer Academic Publishers.
- Zweig M.H., Campbell G. ROC Plots: A Fundamental Evaluation Tool in Clinical Medicine // Clinical Chemistry, Vol. 39, No. 4, 1993.
- Davis J., Goadrich M. The Relationship Between Precision-Recall and ROC Curves // Proc. Of 23 International Conference on Machine Learning, Pittsburgh, PA, 2006.
Другие материалы по теме:
Применение логистической регрессии в медицине и скоринге
Machine learning в Loginom на примере задачи c Kaggle
Смотрите также
 Внедрение элементов Индустрии 4.0: «Умный карьер». Вебинар
Внедрение элементов Индустрии 4.0: «Умный карьер». Вебинар  Loginom Scorecard Modeler. Построение скоринговых карт. Деморолик
Loginom Scorecard Modeler. Построение скоринговых карт. Деморолик  Самоорганизующиеся карты Кохонена — математический аппарат
Самоорганизующиеся карты Кохонена — математический аппарат  Английская версия Loginom
Английская версия Loginom  Прогнозирование аварий и обнаружение потерь на объектах газоснабжения. Вебинар
Прогнозирование аварий и обнаружение потерь на объектах газоснабжения. Вебинар  Простой визуальный ETL для BI. Интеграция Loginom и Visiology. Вебинар
Простой визуальный ETL для BI. Интеграция Loginom и Visiology. Вебинар 这篇关于threshold的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!