最大子列和算法

本文主要是介绍最大子列和算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

作者：whj95

算法一：双边界单扫描

　　该算法为三变量三循环，
　　核心思想：分别设两个变量确立左边界和右边界，然后再用一个变量当做光标从左边界到右边界扫描求和。
　　伪码：

int maxsubseqsum（const int A[],int N）
{循环体（i,i < N,i++）循环体（j=i,j < N;j++）抛弃当前和循环体（k=i;k<=j;k++）维护当前和与最大和
}

　　C++参考代码如下：

int maxsubseqsum(const int A[],int N)
{int thissum = 0,maxsum = 0;for(int i = 0; i <N; i++)for(int j = i; j < N; j++){thissum = 0;//每次更新边界抛弃之前的thisum值for(int k = i; k <= j; k++)thissum += A[k];if(thissum > maxsum)maxsum = thissum;}return maxsum;
}

　　缺陷：所谓光标设置完全没有用，时间复杂度T(N) = O(N $^3$ )达到了比较恐怖的时间。

算法二：单边界单扫描

　　该算法为双变量双循环，
　　核心思想：设一个变量为左边界，另一个变量从左边界往后扫描即可。
　　伪码：

int maxsubseqsum（const int A[],int N）
{循环体（i,i < N,i++）抛弃当前和循环体（j=i,j < N;j++）维护当前和与最大和
}

　　C++参考代码如下：

int maxsubseqsum(const int A[],int N)
{int thissum = 0,maxsum = 0;for(int i = 0; i < N; i++){thisnum = 0;//每次更新边界抛弃之前的thisum值for(int j = i; j < N; j++)thissum += A[j];if(thissum > maxsum)maxsum = thissum;}return maxsum;
}

　　缺陷：时间复杂度为T(N) = O(N $^2$ )还是不够优，考虑如何降到O(NlogN)，于是有了算法三。
　　

算法三：分治法

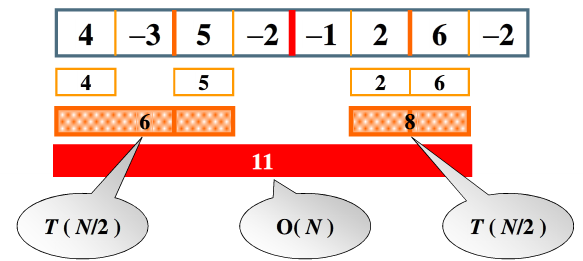
　这里写图片描述
　　图片源于浙大陈越老师的数据结构课件
　　可将问题分治，即分解为规模更小的类似的问题：每次将子列对半拆分，最大子列即为max(①最大左子列②最大右子列③横跨划分线的最大子列)
　　伪码：

int maxsubseqmax(int A[],int left,int right)
{/*递归部*/递归基类左子列递归，右子列递归/*跨越中部的情况*/循环体{维护当前子列和与最大子列和和}//中部向左最大子列循环体{维护当前子列和与最大子列和和}//中部向右最大子列/*三分归一*/返回max(最大左子列，最大右子列，中部向左最大子列+中部向右最大子列)
}

　　C++参考代码如下：

int maxsubseqsum(int A[],int left,int right)
{/*递归基准*/if(left == right){if(A[left] > 0)return A[left];elsereturn 0;}/*左半边右半边递归*/int center = (left + right) / 2;int maxLeftSum = maxsubseqsum(A,left,center);int maxRightSum = maxsubseqsum(A,center + 1,right);/*穿过中部的子列 = 中部往左最大子列+中部往右最大子列*/int thisLeftBorderSum = 0,maxLeftBorderSum = 0;for(int i = center; i >= left; i--){thisLeftBorderSum += A[i];if(thisLeftBorderSum > maxLeftBorderSum)maxLeftBorderSum = thisLeftBorderSum;}for(int i = center + 1; i >= right; i++){thisRightBorderSum += A[i];if(thisRightBorderSum > maxRightBorderSum)maxRightBorderSum = thisRightBorderSum;}return max3(maxLeftSum,maxRightSum,maxLeftBorderSum + maxRightBorderSum);
}/*三分归一*/
int max3(int a,int b,int c)
{int max = 0;if(a > b)max= a;elsemax = b;max = (max,c)?max:c;return max;
}

　　缺陷：相比以上两种算法，该算法拥有足够优秀的时间复杂度T(N) = O(NlogN)。推导如下：T(N) = 2T(N/2)+cN = 2[2T(N/2 $^2$ ) + cN/2] + cN = 2 $^k$ O(1) + ckN
　　∵N/2 $^k$ = 1
　　∴k = log $_2$ N
　　即T(N) = O(NlogN)
　　但由于算法四达到了线性时间，所以此算法还并非最优算法。其实该算法在递归基准中也蕴含了算法四的思想。

算法四：单变量在线处理

　　核心思想：最大子列和要求的是连续和最大。既然连续则扫到的当前子列可以看成一个数，而要求最大则每次维护的当前子列和不能为负（注：不是指单个元素不能为负），否则舍去。
　　伪码：

int maxsubseqsum(const int A[],int N)
{循环体{当前子列和 += A[i];if(当前子列和>=0)维护当前子列和与最大子列和if(当前子列和<0)舍去当前子列和（令当前子列和=0）}
}

　　C++参考代码如下：

int maxsubseqsum(const int A[],int N)
{int thissum = 0,maxsum = 0;for(int i = 0; i < N; i++){thissum += A[i];if(thissum > maxsum)maxsum = thissum;if(thissum < 0)thissum = 0;}
}