代码随想录算法训练营第十八天 | 前中后序构造二叉树

513.找树左下角的值

        这道题依然可以用递归和迭代两种方法来做，与以往不同的是，这道题用迭代会更简单一些

递归

如果使用递归法，如何判断是最后一行呢，其实就是深度最大的叶子节点一定是最后一行。

所以要找深度最大的叶子节点。

那么如何找最左边的呢？可以使用前序遍历（当然中序，后序都可以，因为本题没有 中间节点的处理逻辑，只要左优先就行），保证优先左边搜索，然后记录深度最大的叶子节点，此时就是树的最后一行最左边的值。

递归三部曲：

• 确定递归函数的参数和返回值

参数必须有要遍历的树的根节点，还有就是一个int型的变量用来记录最长深度。 这里就不需要返回值了，所以递归函数的返回类型为void。

本题还需要类里的两个全局变量，maxLen用来记录最大深度，result记录最大深度最左节点的数值。

代码如下：

int maxDepth = INT_MIN;   // 全局变量 记录最大深度
int result;       // 全局变量 最大深度最左节点的数值
void traversal(TreeNode* root, int depth)

• 确定终止条件

当遇到叶子节点的时候，就需要统计一下最大的深度了，所以需要遇到叶子节点来更新最大深度。

代码如下：

if (root->left == NULL && root->right == NULL) {if (depth > maxDepth) {maxDepth = depth;           // 更新最大深度result = root->val;   // 最大深度最左面的数值}return;
}

• 确定单层递归的逻辑

在找最大深度的时候，递归的过程中依然要使用回溯，代码如下：

                    // 中
if (root->left) {   // 左depth++; // 深度加一traversal(root->left, depth);depth--; // 回溯，深度减一
}
if (root->right) { // 右depth++; // 深度加一traversal(root->right, depth);depth--; // 回溯，深度减一
}
return;

完整代码如下：

class Solution {
public:int maxDepth = INT_MIN;int result;void traversal(TreeNode* root, int depth) {if (root->left == NULL && root->right == NULL) {if (depth > maxDepth) {maxDepth = depth;result = root->val;}return;}if (root->left) {depth++;traversal(root->left, depth);depth--; // 回溯}if (root->right) {depth++;traversal(root->right, depth);depth--; // 回溯}return;}int findBottomLeftValue(TreeNode* root) {traversal(root, 0);return result;}
};

当然回溯的地方可以精简，精简代码如下：

class Solution {
public:int maxDepth = INT_MIN;int result;void traversal(TreeNode* root, int depth) {if (root->left == NULL && root->right == NULL) {if (depth > maxDepth) {maxDepth = depth;result = root->val;}return;}if (root->left) {traversal(root->left, depth + 1); // 隐藏着回溯}if (root->right) {traversal(root->right, depth + 1); // 隐藏着回溯}return;}int findBottomLeftValue(TreeNode* root) {traversal(root, 0);return result;}
};

迭代法

本题使用层序遍历再合适不过了，比递归要好理解得多！

只需要记录最后一行第一个节点的数值就可以了。

代码如下：

class Solution {
public:int findBottomLeftValue(TreeNode* root) {queue<TreeNode*> que;if (root != NULL) que.push(root);int result = 0;while (!que.empty()) {int size = que.size();for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();if (i == 0) result = node->val; // 记录最后一行第一个元素if (node->left) que.push(node->left);if (node->right) que.push(node->right);}}return result;}
};

总结

本题涉及如下几点：

• 递归求深度的写法，我们在110.平衡二叉树 (opens new window)中详细的分析了深度应该怎么求，高度应该怎么求。
• 递归中其实隐藏了回溯，在257. 二叉树的所有路径 (opens new window)中讲解了究竟哪里使用了回溯，哪里隐藏了回溯。
• 层次遍历，在二叉树：层序遍历登场！ (opens new window)深度讲解了二叉树层次遍历。 所以本题涉及到的点，我们之前都讲解过，这些知识点需要同学们灵活运用，这样就举一反三了。

112. 路径总和

可以使用深度优先遍历的方式（本题前中后序都可以，无所谓，因为中节点也没有处理逻辑）来遍历二叉树

• 确定递归函数的参数和返回类型

参数：需要二叉树的根节点，还需要一个计数器，这个计数器用来计算二叉树的一条边之和是否正好是目标和，计数器为int型。

再来看返回值，递归函数什么时候需要返回值？什么时候不需要返回值？这里总结如下三点：

• 如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。（这种情况就是本文下半部分介绍的113.路径总和ii）
• 如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。 （这种情况我们在236. 二叉树的最近公共祖先 (opens new window)中介绍）
• 如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。（本题的情况）

而本题我们要找一条符合条件的路径，所以递归函数需要返回值，及时返回，那么返回类型是什么呢？

如图所示：

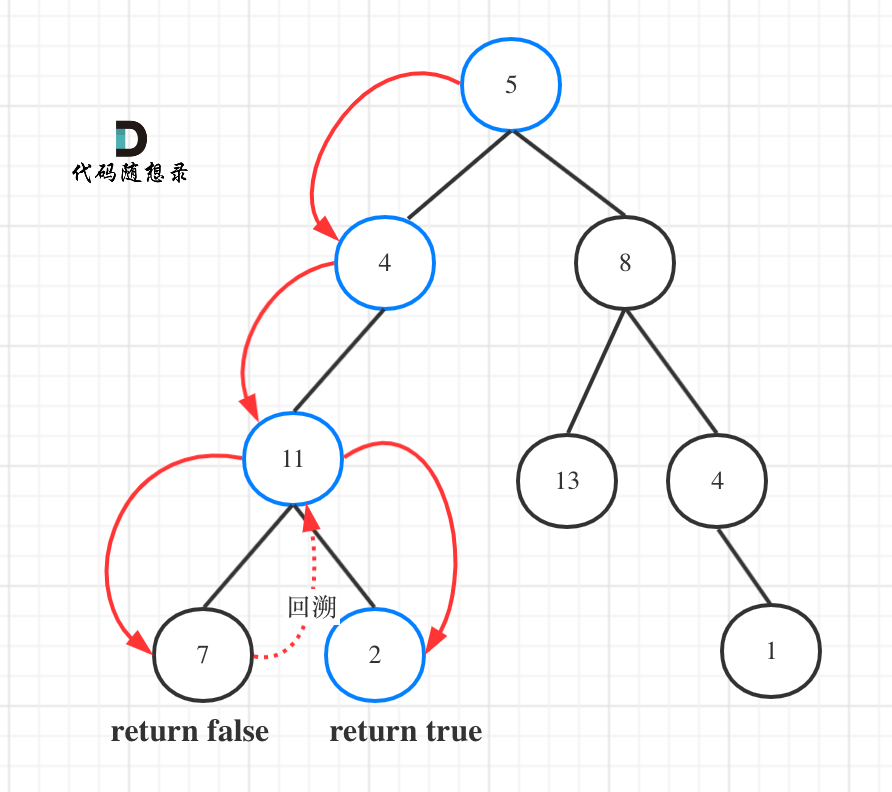
图中可以看出，遍历的路线，并不要遍历整棵树，所以递归函数需要返回值，可以用bool类型表示。

所以代码如下：

bool traversal(treenode* cur, int count)   // 注意函数的返回类型

• 确定终止条件

首先计数器如何统计这一条路径的和呢？

不要去累加然后判断是否等于目标和，那么代码比较麻烦，可以用递减，让计数器count初始为目标和，然后每次减去遍历路径节点上的数值。

如果最后count == 0，同时到了叶子节点的话，说明找到了目标和。

如果遍历到了叶子节点，count不为0，就是没找到。

递归终止条件代码如下：

if (!cur->left && !cur->right && count == 0) return true; // 遇到叶子节点，并且计数为0
if (!cur->left && !cur->right) return false; // 遇到叶子节点而没有找到合适的边，直接返回

• 确定单层递归的逻辑

因为终止条件是判断叶子节点，所以递归的过程中就不要让空节点进入递归了。

递归函数是有返回值的，如果递归函数返回true，说明找到了合适的路径，应该立刻返回。

代码如下：

if (cur->left) { // 左 （空节点不遍历）// 遇到叶子节点返回true，则直接返回trueif (traversal(cur->left, count - cur->left->val)) return true; // 注意这里有回溯的逻辑
}
if (cur->right) { // 右 （空节点不遍历）// 遇到叶子节点返回true，则直接返回trueif (traversal(cur->right, count - cur->right->val)) return true; // 注意这里有回溯的逻辑
}
return false;

以上代码中是包含着回溯的，没有回溯，如何后撤重新找另一条路径呢。

回溯隐藏在traversal(cur->left, count - cur->left->val)这里， 因为把count - cur->left->val 直接作为参数传进去，函数结束，count的数值没有改变。

为了把回溯的过程体现出来，可以改为如下代码：

if (cur->left) { // 左count -= cur->left->val; // 递归，处理节点;if (traversal(cur->left, count)) return true;count += cur->left->val; // 回溯，撤销处理结果
}
if (cur->right) { // 右count -= cur->right->val;if (traversal(cur->right, count)) return true;count += cur->right->val;
}
return false;

整体代码如下：

class Solution {
private:bool traversal(TreeNode* cur, int count) {if (!cur->left && !cur->right && count == 0) return true; // 遇到叶子节点，并且计数为0if (!cur->left && !cur->right) return false; // 遇到叶子节点直接返回if (cur->left) { // 左count -= cur->left->val; // 递归，处理节点;if (traversal(cur->left, count)) return true;count += cur->left->val; // 回溯，撤销处理结果}if (cur->right) { // 右count -= cur->right->val; // 递归，处理节点;if (traversal(cur->right, count)) return true;count += cur->right->val; // 回溯，撤销处理结果}return false;}public:bool hasPathSum(TreeNode* root, int sum) {if (root == NULL) return false;return traversal(root, sum - root->val);}
};

以上代码精简之后如下：

class Solution {
public:bool hasPathSum(TreeNode* root, int sum) {if (!root) return false;if (!root->left && !root->right && sum == root->val) {return true;}return hasPathSum(root->left, sum - root->val) || hasPathSum(root->right, sum - root->val);}
};

class Solution {
private:TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {if (postorder.size() == 0) return NULL;// 后序遍历数组最后一个元素，就是当前的中间节点int rootValue = postorder[postorder.size() - 1];TreeNode* root = new TreeNode(rootValue);// 叶子节点if (postorder.size() == 1) return root;// 找到中序遍历的切割点int delimiterIndex;for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {if (inorder[delimiterIndex] == rootValue) break;}// 切割中序数组// 左闭右开区间：[0, delimiterIndex)vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);// [delimiterIndex + 1, end)vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );// postorder 舍弃末尾元素postorder.resize(postorder.size() - 1);// 切割后序数组// 依然左闭右开，注意这里使用了左中序数组大小作为切割点// [0, leftInorder.size)vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());// [leftInorder.size(), end)vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());root->left = traversal(leftInorder, leftPostorder);root->right = traversal(rightInorder, rightPostorder);return root;}
public:TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {if (inorder.size() == 0 || postorder.size() == 0) return NULL;return traversal(inorder, postorder);}
};