1277：【例9.21】方格取数

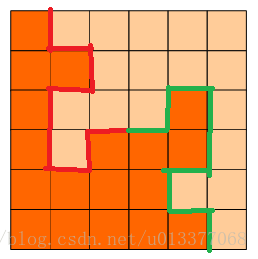
本文主要是介绍1277：【例9.21】方格取数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【算法分析】
 动态规划：坐标型动规
1. 状态定义
阶段：第一趟走到的位置(i,j)与第二趟走到的位置(k,l)
决策：第一趟如何走，同时第二趟如何走
策略：第一趟从(1,1)走到(i,j)，第二趟从(1,1)走到(k,l)的路径。
策略集合：第一趟从(1,1)走到(i,j)，第二趟从(1,1)走到(k,l)的所有路径方案。
条件：取到的数字加和最大
统计量：数字加和
状态定义：dp[i][j][k][l]:第一趟从(1,1)走到(i,j)，第二趟从(1,1)走到(k,l)取到的数字加和最大的路径方案的数字加和。

2. 状态转移方程
记：a[i][j]为(i,j)位置的数字。
分割集合：从(1,1)走到(i,j)，再从(1,1)走到(k,l)的路径方案
由于每次只能向右或下走，那么第一趟走到(i,j)前，只可能在(i,j)上面一格(i-1,j)或左侧一格(i,j-1)。同理，第二趟走到(k,l)前，只可能在(k-1,l)或(k,l-1)。
因此，第一趟到达(i,j)前的位置与第二趟到达(k,l)前的位置就有4种组合:

(i-1,j)与(k-1,l)
(i,j-1)与(k-1,l)
(i-1,j)与(k,l-1)
(i,j-1)与(k,l-1)
先求出第一趟到达(i,j)前的位置与第二趟到达(k,l)前的位置的路线上的数字加和，如果(i,j)与(k,l)不是同一位置，就加上a[i][j]与a[k][l]，否则只加上a[i][j]，即为第一趟到达(i,j)与第二趟到达(k,l)的路线上是数字加和。多种情况求最大值。
详细情况如下：
如果如果(i,j)与(k,l)是同一位置：

第一趟到达(i-1,j)后到达(i,j)，第二趟到达(k-1,l)后到达(k,l)，数字加和为dp[i][j][k][l]=dp[i-1][j][k-1][l]+a[i][j]
第一趟到达(i,j-1)后到达(i,j)，第二趟到达(k-1,l)后到达(k,l)，数字加和为dp[i][j][k][l]=dp[i][j-1][k-1][l]+a[i][j]
第一趟到达(i-1,j)后到达(i,j)，第二趟到达(k,l-1)后到达(k,l)，数字加和为dp[i][j][k][l]=dp[i-1][j][k][l-1]+a[i][j]
第一趟到达(i,j-1)后到达(i,j)，第二趟到达(k,l-1)后到达(k,l)，数字加和为dp[i][j][k][l]=dp[i][j-1][k][l-1]+a[i][j]
以上四种情况取最大值。
如果(i,j)与(k,l)不是同一位置：

第一趟到达(i-1,j)后到达(i,j)，第二趟到达(k-1,l)后到达(k,l)，数字加和为dp[i][j][k][l]=dp[i-1][j][k-1][l]+a[i][j]+a[k][l]
第一趟到达(i,j-1)后到达(i,j)，第二趟到达(k-1,l)后到达(k,l)，数字加和为dp[i][j][k][l]=dp[i][j-1][k-1][l]+a[i][j]+a[k][l]
第一趟到达(i-1,j)后到达(i,j)，第二趟到达(k,l-1)后到达(k,l)，数字加和为dp[i][j][k][l]=dp[i-1][j][k][l-1]+a[i][j]+a[k][l]
第一趟到达(i,j-1)后到达(i,j)，第二趟到达(k,l-1)后到达(k,l)，数字加和为dp[i][j][k][l]=dp[i][j-1][k][l-1]+a[i][j]+a[k][l]
以上四种情况取最大值。

【参考代码】
 

#include <bits/stdc++.h>
using namespace std;
#define N 11
int dp[N][N][N][N], a[N][N];//dp[i][j][k][l]:第一趟从(1,1)走到(i,j)，第二趟从(1,1)走到(k,l)取到的数字加和最大的方案的数字加和。
int main()
{int n, l, r, v;//l:行 r:列 v:值cin >> n;while(cin >> l >> r >> v) {if(l == 0 && r == 0 && v == 0)break;a[l][r] = v;       }for(int i = 1; i <= n; ++i)for(int j = 1; j <= n; ++j)for(int k = 1; k <= n; ++k)for(int l = 1; l <= n; ++l){if(k == i && l == j)//如果是同一位置 dp[i][j][k][l] = max(max(dp[i-1][j][k-1][l], dp[i-1][j][k][l-1]), max(dp[i][j-1][k-1][l], dp[i][j-1][k][l-1])) + a[i][j];else//如果不是同一位置 dp[i][j][k][l] = max(max(dp[i-1][j][k-1][l], dp[i-1][j][k][l-1]), max(dp[i][j-1][k-1][l], dp[i][j-1][k][l-1])) + a[i][j] + a[k][l];       }cout << dp[n][n][n][n];return 0;
}

这篇关于1277：【例9.21】方格取数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---