技术背景
JAX-MD是一款基于JAX的纯Python高性能分子动力学模拟软件,应该说在纯Python的软件中很难超越其性能。当然,比一部分直接基于CUDA的分子动力学模拟软件性能还是有些差距。而在计算过程中,近邻表的计算是占了较大时间和空间比重的模块,我们通过源码分析,看看JAX-MD中使用了哪些的奇技淫巧,感兴趣的童鞋可以直接参考JAX-MD下的partition模块。
Verlet List和Cell List的使用
关于Verlet List,其实更多的是使用在动力学模拟的过程中,而Cell List则更常用于近邻表的计算优化,也就是我们通俗所说的打格点算法。可以参考下图的一个示例,将一个体系中的多个原子,划分到一个空间中均匀分布的格子里面: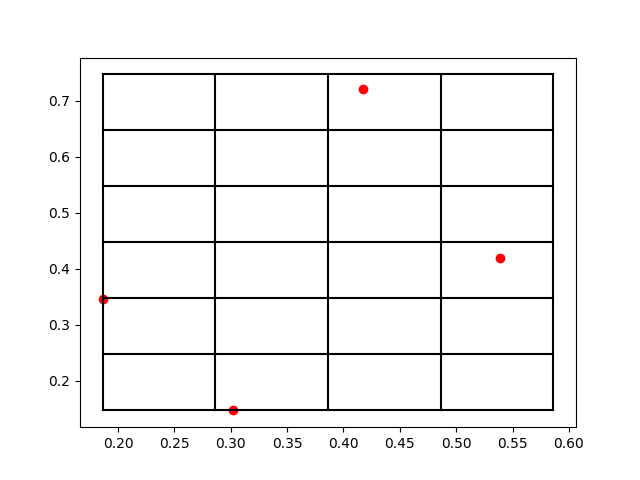
如此一来,我们只需要设定好这些格子的长度,比如长度直接定为判断近邻的cutoff数值,这样我们在计算的过程中,就只需要对当前原子所在格子的周边的格子进行检索即可,大大缩减了计算复杂度。原本不加格子的近邻表计算复杂度为\(O(N^2)\),而加了格子之后近邻表计算的复杂度为\(O(Nlog N)\),其中\(N\)为体系的原子数目。在前面的一篇博客中,我们大致的使用Python中的Numba写了一个简单的打格点算法代码(不包含近邻表的检索),感兴趣的童鞋可以参考一下。
当然,这些都是比较高层次的算法,我们可以阅读JAX-MD中的代码实现,来看看他是怎么一步一步去实现这个算法的。
计算格点长度
在JAX-MD中,周期性盒子的大小是给定的,但是格点大小不是一个固定值,而是先给定一个格点大小的下界,然后计算格点数量并取了一个floor的操作,再根据格点的数量计算得到每个格点的最终大小:
cells_per_side = onp.floor(box_size / minimum_cell_size)
cell_size = box_size / cells_per_side
cells_per_side = onp.array(cells_per_side, dtype=i32)
cell_count = reduce(mul, flat_cells_per_side, 1)这里使用的floor操作确保了最终的cell_size一定是大于给定的minimum_cell_size的。这里还有一行代码用于计算总的格点数,这里用了一个非常优雅的实现,是functools中的reduce方法,其实实现的内容就将数组中的元素按照给定的函数逐两个的叠加计算,可以参考详细说明:
def reduce(function, sequence, initial=_initial_missing):"""reduce(function, sequence[, initial]) -> valueApply a function of two arguments cumulatively to the items of a sequence,from left to right, so as to reduce the sequence to a single value.For example, reduce(lambda x, y: x+y, [1, 2, 3, 4, 5]) calculates((((1+2)+3)+4)+5). If initial is present, it is placed before the itemsof the sequence in the calculation, and serves as a default when thesequence is empty."""或者用一个更加贴合算法中示例的代码来说明下更简单些:
In [1]: from operator import mulIn [2]: from functools import reduceIn [3]: reduce(mul,[4,5,6],1)
Out[3]: 120In [4]: reduce(mul,[4,5,6],2)
Out[4]: 240最后一个输入给定的initial值是一个基础值。
哈希乘子
在JAX-MD的源码中称之为哈希常量,我们可以先简单的描述下这个乘子的作用场景:在前面介绍的打格点算法中,每一个原子会获得1个格点的编号,如果是在三维空间,这个编号中会包含3个元素,分别对应\((x,y,z)\)三个轴方向的格点编号。但是如果我们需要确认“2个不同的原子是否在同一个格子中?目标原子在具体哪一个格子中?指定的格子中有几个原子?”这些问题的话,我们最好是将一个三维的格点转换成一维的格点排列。比如一个\(10\times10\times10\)的网格,其中\((0,0,0)\)号网格就会被编码成第0个网格,第\((0,1,0)\)号网格会被编码成第10个网格,第\((0,0,1)\)号网格会被编码成第100个网格。换句话说,要实现这个三维到一维的转化,每一个维度都会带有不同大小的权重,这个权重值,就是我们所谓的哈希乘子:
one = jnp.array([[1]], dtype=i32)
cells_per_side = jnp.concatenate((one, cells_per_side[:, :-1]), axis=1)
hash_constant = jnp.array(jnp.cumprod(cells_per_side), dtype=i32)也可以用一个更加浅显的示例来展示下这个计算的过程:
In [5]: import numpy as npIn [6]: one = np.array([[1]],dtype=np.int32)In [7]: cells_per_side = np.array([[10,20,30]])In [8]: cells_per_side = np.concatenate((one,cells_per_side[:,:-1]),axis=1)In [9]: cells_per_side
Out[9]: array([[ 1, 10, 20]])In [10]: np.cumprod(cells_per_side)
Out[10]: array([ 1, 10, 200])先是完成了一个维度替换,再是累计做乘法,最后再放到具体编号列表中一点乘,不同的原子如果在同一个格点中,就会得到相同的计算结果。还有一点说明是,在将3维的格点转化成1维格点之后,如果需要再转化回3维的格点,只需要一个reshape即可。
格点原子数统计
获得每个原子对应的格点编号是容易的,通过广播机制直接一步就可以计算出来。而上一步中我们提到了哈希乘子,在这里就要派上用场,得到每个原子所在的格点编号,然后做一个段求和的操作,就可以得到每个格点中对应的原子数目:
particle_index = jnp.array(position / cell_size, dtype=i32)
particle_hash = jnp.sum(particle_index * hash_multipliers, axis=1)
filling = ops.segment_sum(jnp.ones_like(particle_hash),particle_hash,cell_count)关于这里面使用到的段求和操作,可以参考如下图片(图片来自于参考链接2)所表示的算法过程: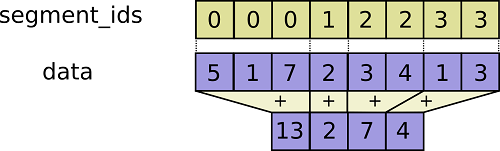
在得到每个格点中的原子数之后,还有一个很重要的意义是我们可以以其中最大的原子数作为计算近邻表的一个padding长度的基准。我们很难在python之中去高效的处理循环,尽可能是直接使用numpy和jax所集成的操作,而这些操作的对象都要求维度上的统一,因此我们需要一个padding的操作,保障每一个原子的近邻表size一致。当然,这里面多出来的位置可以用非合法值进行填充,常用的有-1等。
获取近邻格点编号
因为在近邻检索过程中,我们只检索当前原子的近邻格点中的原子。对于一维的体系,只需要检索2个周边格点即可,对于2维的体系,需要检索周边的8个格点,而对于3维的体系,需要检索周边的26个格点。在JAX-MD中使用了ndindex的迭代器来生成近邻格点的id:
for dindex in onp.ndindex(*([3] * dimension)):yield onp.array(dindex, dtype=i32) - 1其实实现的效果与itertools.product是一致的:
In [11]: from itertools import productIn [12]: product(range(3),repeat=3)
Out[12]: <itertools.product at 0x7f79a3035fc0>In [13]: list(product(range(3),repeat=3))
Out[13]:
[(0, 0, 0),(0, 0, 1),(0, 0, 2),(0, 1, 0),(0, 1, 1),(0, 1, 2),(0, 2, 0),(0, 2, 1),(0, 2, 2),(1, 0, 0),(1, 0, 1),(1, 0, 2),(1, 1, 0),(1, 1, 1),(1, 1, 2),(1, 2, 0),(1, 2, 1),(1, 2, 2),(2, 0, 0),(2, 0, 1),(2, 0, 2),(2, 1, 0),(2, 1, 1),(2, 1, 2),(2, 2, 0),(2, 2, 1),(2, 2, 2)]当然,这个得到的id列表还需要进一步的操作,比如全部-1,就可以将中心的格点id变成\((0,0,0)\),考虑近邻元素时,需要忽略自身跟自身的近邻,再有就是,转化成一维之后的格点id,还需要多乘一个上面提到过的哈希乘子。
GPU的循环链表
因为GPU上的计算模式的特殊性,加上JAX的封装,我们很难去构造一些真实意义的数据结构,比如链表、栈和队列等等。那么当我们需要类似的功能的时候,就只能用矩阵移位的方法:
def _shift_array(arr: Array, dindex: Array) -> Array:if len(dindex) == 2:dx, dy = dindexdz = 0elif len(dindex) == 3:dx, dy, dz = dindexif dx < 0:arr = jnp.concatenate((arr[1:], arr[:1]))elif dx > 0:arr = jnp.concatenate((arr[-1:], arr[:-1]))if dy < 0:arr = jnp.concatenate((arr[:, 1:], arr[:, :1]), axis=1)elif dy > 0:arr = jnp.concatenate((arr[:, -1:], arr[:, :-1]), axis=1)if dz < 0:arr = jnp.concatenate((arr[:, :, 1:], arr[:, :, :1]), axis=2)elif dz > 0:arr = jnp.concatenate((arr[:, :, -1:], arr[:, :, :-1]), axis=2)return arr比如正常的一个循环链表,应该是有一个指针来读取下一个元素的,只是最后一个元素又指向了第一个元素,因此形成了一个如下图(图片来自于参考链接3)所示的循环链表:
那么在JAX中去实现循环链表时,我们只能将头部元素转接到尾部去,也就是这里JAX-MD所使用的方法。
排序
由于在前面的计算中,3维的格点编号被转换成了1维,因此我们就可以根据格点编号对坐标等参量同步进行排序:
indices = jnp.array(position / cell_size, dtype=i32)
hashes = jnp.sum(indices * hash_multipliers, axis=1)
sort_map = jnp.argsort(hashes)
sorted_position = position[sort_map]
sorted_hash = hashes[sort_map]
sorted_id = particle_id[sort_map]这里JAX-MD是直接用了argsort的功能,排序后只返回对应排序的一个映射id,这样就可以把排序关系同步到其他的参数如坐标中。再获得到排序之后,再初始化一个格点数*格点容量的cell_position和cell_id,再逐一将排序之后的position和id填进去,得到一个可能为稀疏的cell_list:
sorted_cell_id = jnp.mod(lax.iota(i32, N), cell_capacity)
sorted_cell_id = sorted_hash * cell_capacity + sorted_cell_id
cell_position = cell_position.at[sorted_cell_id].set(sorted_position)
cell_id = cell_id.at[sorted_cell_id].set(sorted_id)在Jax中是不支持原位操作的,需要使用Jax的object.at[id].set(value)这样的功能模块来实现。而在JAX-MD中大量的使用了一个叫lax.iota的操作,其实这个操作就相当于numpy.arange,但是不清楚为什么非得用这个函数,于是测试了下几个方案的速度:
In [1]: from jax import laxIn [2]: from jax import numpy as jnpIn [3]: import numpy as npIn [4]: %timeit np.arange(1000000,dtype=np.int32)
377 µs ± 2 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)In [5]: %timeit jnp.arange(1000000,dtype=jnp.int32)
118 µs ± 53.9 µs per loop (mean ± std. dev. of 7 runs, 1 loop each)In [6]: %timeit lax.iota(jnp.int32,1000000)
52.6 µs ± 402 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)结果我们发现lax.iota这个操作的速度确实是快于使用jnp.arange的,只是看起来还不太习惯。
构建Neighbor List
在上一步完成了格点近邻表的构建之后,开始正式搜索每个原子的近邻表。那么在定义原子的近邻原子时,我们就需要给定一个cutoff值,当原子距离小于这个值时,我们就认为这一对原子是近邻原子。但是这里就有一个关联性的问题,我们通过打格点的方法来搜索近邻表,那么格点大小的选取,是否要与cutoff的值相关呢?在JAX-MD中,直接选取了cutoff的值作为格点大小(实际上是cutoff加上一个松弛小量dr_threshold,在松弛范围内不改变近邻关系,所以不影响这部分的算法复杂性推断):
cell_size = cutoff关于Cell Size选取的思考
至于为什么这样选取,我们可以做一个简单的思考。如果\(cutoff<cell\_size\),那么就意味着,我们同样需要在3维空间搜索27个格子中的近邻原子,只是每个格子中的平均原子数更多了,但是这其实相当于做了更多的无用功,所以我们选择cell_size时最好不要超过cutoff的值。而如果是\(cutoff>cell\_size\)的情况,相对而言就比较复杂,比如当\(cutoff=2cell\_size\)时,相当于要在空间中搜索125个盒子,当然,每个盒子中的平均原子数也随之下降了,这就看具体的取舍了。在算法中我们知道,对于一个有序的数组的搜索复杂性是\(O(log\ n)\)的。那么一个比较粗糙的估计下的结果就是(如下图所示),格点长度取半长的cutoff可以达到一个相对更低的复杂性,不过一般还是得具体情况具体分析,至少我们现在已经知道,JAX-MD是直接取了cutoff的长度作为格点长度。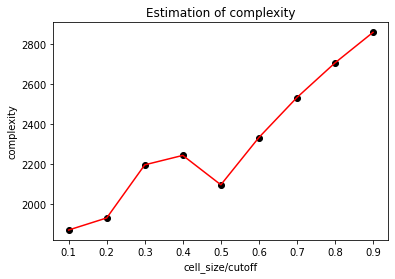
上图用于估计复杂度的代码如下所示:
import matplotlib.pyplot as plt
import numpy as npN = 300
l = 1.
c = 0.3
s = np.arange(0.1,1,0.1)*c
y = N*np.log2((np.ceil(c/s)*2+1)**3*N*s**3/l**3)
plt.figure()
plt.title('Estimation of complexity')
plt.xlabel('cell_size/cutoff')
plt.ylabel('complexity')
plt.plot(s/c,y,'o',color='black')
plt.plot(s/c,y,color='red')
plt.show()Neighbor List的初始化
在JAX-MD的源码中又学到了一个扩维的小技巧,可以使用array[None,:]的形式来替代numpy.expand_dims,输出是完全一样的,关键是速度要快上10倍:
In [1]: import numpy as npIn [2]: a=np.arange(10)In [3]: a[None,:]
Out[3]: array([[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]])In [4]: np.expand_dims(a,axis=0)
Out[4]: array([[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]])In [5]: %timeit b=a[None,:]
164 ns ± 0.774 ns per loop (mean ± std. dev. of 7 runs, 10000000 loops each)In [6]: %timeit b=np.expand_dims(a,axis=0)
2.43 µs ± 9.05 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)一般机器学习框架中都会经常用到扩维这个函数,目前并不确定这个算子加速是否适用于所有的框架,至少在numpy和jax里面我们发现应该是适用的。
总结概要
本文是第一篇关于JAX-MD的源码学习的文章,主要关注点在于JAX-MD中对于近邻表的检索和优化。本文的主要内容是其中构建CellList的部分,通过打格点的方法可以大大降低近邻表搜索算法的复杂度,在GPU计算的过程中更是可以极大的降低显存的占用,从而允许我们去运行更大规模的体系。
版权声明
本文首发链接为:https://www.cnblogs.com/dechinphy/p/jaxnb1.html
作者ID:DechinPhy
更多原著文章请参考:https://www.cnblogs.com/dechinphy/
打赏专用链接:https://www.cnblogs.com/dechinphy/gallery/image/379634.html
腾讯云专栏同步:https://cloud.tencent.com/developer/column/91958
参考链接
- https://github.com/google/jax-md
- https://www.w3cschool.cn/tensorflow_python/tensorflow_python-ua7w2jip.html
- http://data.biancheng.net/view/7.html







