本文主要是介绍2020 ICPC·小米邀请赛 决赛 J. Rikka with Book(状压dp),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目
登录—专业IT笔试面试备考平台_牛客网
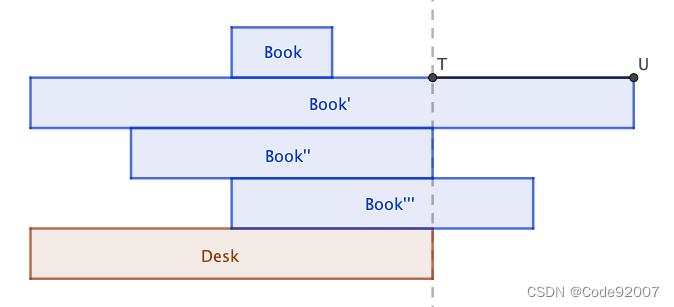
n(n<=20)本书,放在桌子上,
第i本书的可以看成是li(li<=1e3)*1*1的物体,其中长为li,宽为1,高为1,
质量均匀分布,且为wi(wi<=1e3)
求n本书摞在一起,使得任意一本书都不掉下桌子时,书能伸出桌沿的长度的最大值是多少
思路来源
官方题解&申老师
题解
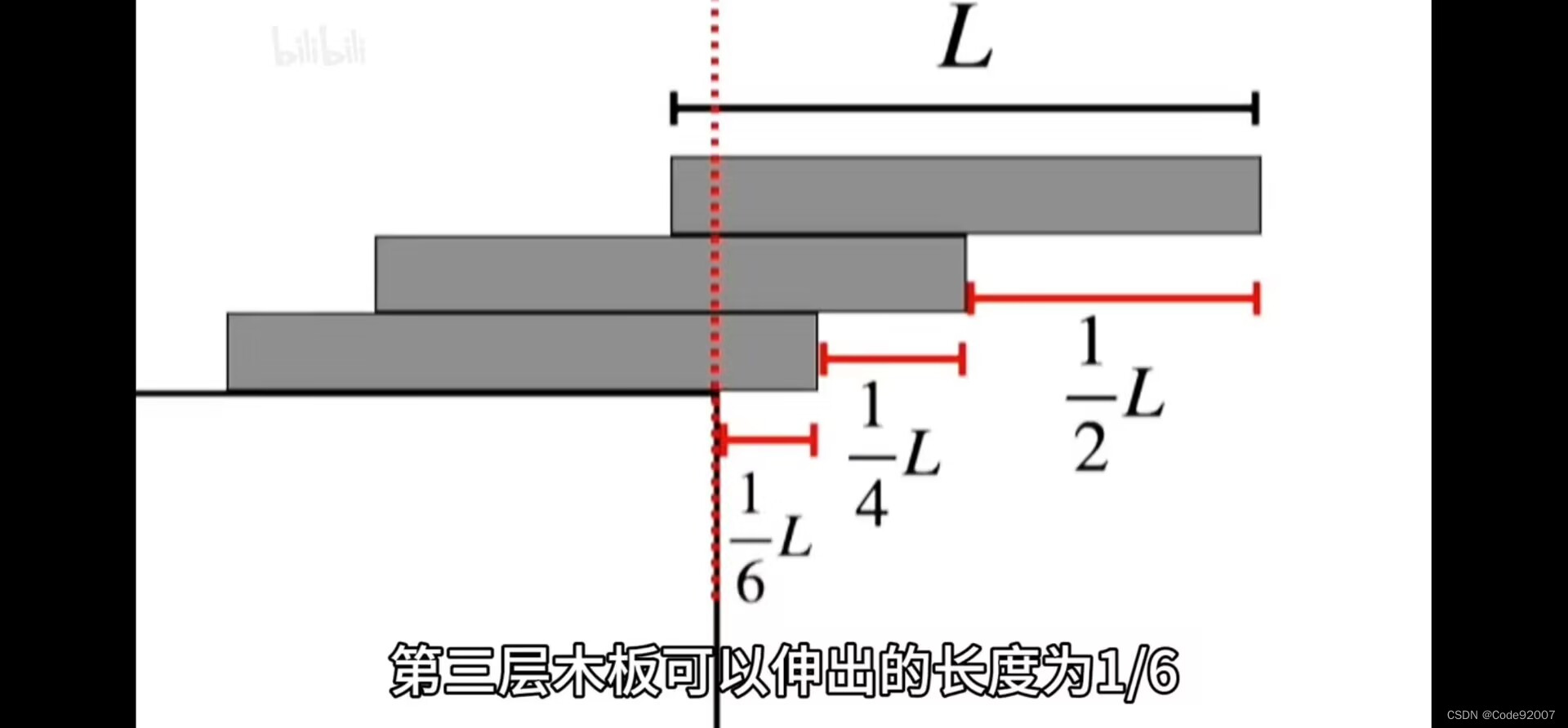
放的话肯定是从上往下放,这样已经放上去的可以看成是一个物体,
并且当b物品摞在a物品之上时,一定是把b物品的重心放到a物品的边沿上,
好比把a物品当成桌子,一定是放到桌沿上,
再将a和b看成同一个物品时,一定是放到下一个物品的边沿上,
一旦一个物体的质量和重心的位置确定了,这个物品的其他属性就无关紧要了,从而无后效性
所以状压每次往下垫的书是哪一本,确定放的顺序,关注的是伸出去的最大值
往下垫的书的重心位于l/2处,质量为a;
上面的书看成一体时,重心位于边沿,质量为b
那么新的重心,根据杠杆原理,位于距边沿a/(a+b)的位置,记add=a/(a+b)
记原来的伸出去的最大值为x,则新的最大值为x+add,
此外,可以旋转一下整个物体,使整个物体的重心仍落在边沿上不落下去,
但是伸出边沿的是往下垫的书的另外半边,也就是l-add这半边,二者取max即可
所以,如果最优解是第i本书伸的最远,最上面的书是1,最下面的书是n,
一定是对于j∈[1,i-1]来说,把[1,j]看成一体时,[1,j]的重心压在j+1的左边沿,
对于j∈[i+1,n]来说,将[1,j-1]看成一体时,[1,j-1]的重心压在j的右边沿
每次枚举的时候,旋转or不旋转二选一都试一下,显然可以覆盖这种情况
代码1
维护的是长度l、到左边沿的距离p、整体的质量w
// Problem: Rikka with Book
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/9328/J?&headNav=acm
// Memory Limit: 1048576 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
const int N=20,M=(1<<20)+5;
int n;
db dp[M];
int lb(int x){return x&(-x);
}
struct node{db l,p;//长度 离左侧距离int w;//质量node(){l=0;p=1e7;w=0;}db dis(){return l-p;}void show(int i=-1){printf("i:%d l:%lf p:%lf w:%d\n",i,l,p,w);}
}e[M];
//b放在a上
bool operator>(node a,node b){return a.dis()>b.dis();
}
node mer(node a,node b){db x=a.l-a.p;node c;db B=a.w*x/(a.w+b.w);if(b.p>a.l){//b更左c.l=b.l;c.p=b.p-B;//b.l-b.p+B}else{//a更左c.l=a.l+b.l-b.p;c.p=a.l-B;//b.l-b.p+B}c.w=a.w+b.w;if(c.p>c.l-c.p)c.p=c.l-c.p;//puts("");//a.show();b.show();c.show();//puts("");return c;
}
void sol(){sci(n);rep(i,0,n-1){int x=1<<i;scanf("%lf",&e[x].l);e[x].p=e[x].l/2.0;}rep(i,0,n-1){int x=1<<i;scanf("%d",&e[x].w);}int up=(1<<n)-1;rep(i,1,up){if(lb(i)==i)continue;//printf("i:%d\n",i);rep(j,0,n-1){if(!(i>>j&1))continue;int v=1<<j,oth=i^v;node w=mer(e[v],e[oth]);//只枚举最底下那个是什么if(w>e[i])e[i]=w;//e[oth].p=e[oth].l-e[oth].p;//w=mer(e[v],e[oth]);//if(w>e[i])e[i]=w;//w.show();}//if(e[i].p>e[i].l-e[i].p)e[i].p=e[i].l-e[i].p;//b[1].p=b[1].l-b[1].p;//e[i].show(i);}printf("%.10lf\n",e[up].dis());
}
int main(){sol();return 0;
}代码2(三个顶俩代码)
发现无需维护长度l和距一端的位置p,只维护右半边伸出去的最大值即可
每次尝试一下翻或不翻
#include <bits/stdc++.h>using namespace std;
int n,l[30],w[30],x[1100000];
double f[1100000];int main()
{int i,j;scanf("%d",&n);for(i=0;i<n;i++)scanf("%d",&l[i]);for(i=0;i<n;i++)scanf("%d",&w[i]);for(i=1;i<(1<<n);i++){for(j=0;j<n;j++)if(i&(1<<j))break;x[i]=x[i-(1<<j)]+w[j];}for(i=1;i<(1<<n);i++){for(j=0;j<n;j++)if(i&(1<<j))f[i]=max(f[i],max(f[i^(1<<j)]+double(0.5*w[j]*l[j])/x[i],l[j]-double(0.5*w[j]*l[j])/x[i]));}printf("%.12lf\n",f[(1<<n)-1]);return 0;
}这篇关于2020 ICPC·小米邀请赛 决赛 J. Rikka with Book(状压dp)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



