本文主要是介绍WGAN 优势小结,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
我在上一篇博文为什么 GAN 不好训练中,分析了原始 GAN 难以训练的原因,本篇博文将分析下 WGAN 的优势。
1. Wasserstein 距离
W 是指 Wasserstein,Wasserstein 距离又叫Earth-Mover(EM)距离。Wasserstein距离相比KL散度、JS散度的优越性在于,即便两个分布没有重叠,Wasserstein距离仍然能够反映它们的远近。WGAN本作通过简单的例子展示了这一点。考虑如下二维空间中的两个分布P1和P2,P1在线段AB上均匀分布,P2在线段CD上均匀分布,通过控制参数θ可以控制着两个分布的距离远近。
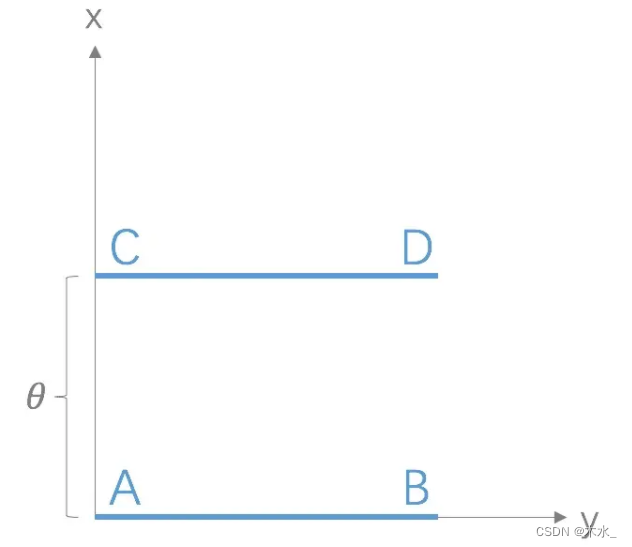

KL 散度和 JS 散度是突变的,要么最大要么最小,Wasserstein 距离却是平滑的,如果我们要用梯度下降法优化 θ 这个参数,前两者根本提供不了梯度,Wasserstein 距离却可以。类似地,在高维空间中如果两个分布不重叠或者重叠部分可忽略,则KL和JS既反映不了远近,也提供不了梯度,但是 Wasserstein 却可以提供有意义的梯度。
2. WGAN 应用
WGAN 的核心思想就是通过数学变换将 Wasserstein 距离写成可求解的形式,利用一个参数数值范围受限的判别器神经网络来最大化这个形式,就可以近似 Wasserstein 距离。在此近似最优判别器下优化生成器使得 Wasserstein 距离缩小,就能有效拉近生成分布与真实分布。
WGAN 的优势如下:
1、彻底解决GAN训练不稳定的问题,不再需要小心平衡生成器和判别器的训练程度。
2、基本解决了collapse mode的问题,确保了生成样本的多样性 。
3、训练过程中终于有一个像交叉熵、准确率这样的数值来指示训练的进程,这个数值越小代表GAN 训练得越好,代表生成器产生的图像质量越高。
4、以上一切好处不需要精心设计的网络架构,最简单的多层全连接网络就可以做到。
实现步骤如下:
1、判别器最后一层去掉 sigmoid。sigmoid 函数容易出现梯度消失的情况。
2、生成器和判别器的 loss 不取 log
3、每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c
4、不要用基于动量的优化算法(包括 momentum 和 Adam),推荐 RMSProp,SGD 也行(原作者的实验经验)
算法流程如下:

这篇关于WGAN 优势小结的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





