DWZ中添加对其它状态的拦截

本文主要是介绍DWZ中添加对其它状态的拦截，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

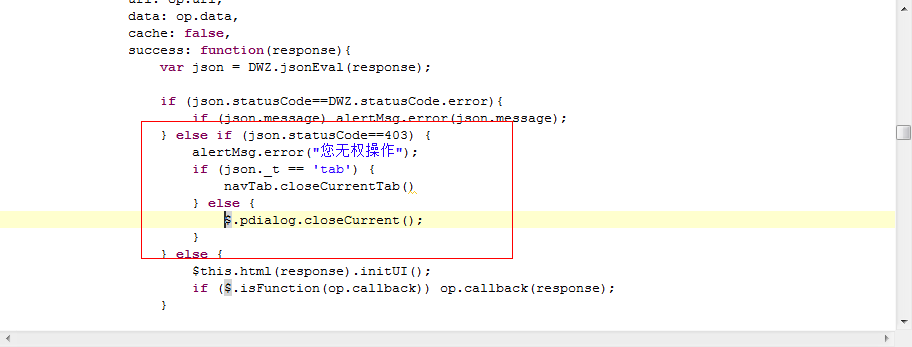
默认DWZ添加了对执行正确、错误以及登录超时的拦截和友好提示，由于需要一个加入权限的东西，想做统一的处理，看了下代码，找到这个地方dwz.cors.js大概192行左右加入下列代码：

红色地方就是我圈出来，加入的。在统一的filter地方根据url判断没权限的话直接返回：

array('statusCode'=>403, 'message'=>'您无权该操作', "navTabId"=>"","forwardUrl"=>"","callbackType"=>"closeCurrent", "_t"=>$this->getRequest()->getParam("_t"))

由于这个地方没办法判断是tab还是dialog，而他们的关闭方式不一样，所以我对每个a都加上了个参数，标明了当前是dialog打开还是tab打开。。没别的好方法了。。我看到下面有个例子

if ($.pdialog) $.pdialog.checkTimeout();
if (navTab) navTab.checkTimeout();

猜测了下是不是判断当前打开的是dialog还是nav，但是我用这个方法不行。。

这篇关于DWZ中添加对其它状态的拦截的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---