L2-043 龙龙送外卖 - java

L2-043 龙龙送外卖

Java (javac)
时间限制
1400 ms
内存限制
256 MB

Python (python3)
时间限制
600 ms
内存限制
64 MB

其他编译器
时间限制
400 ms
内存限制
64 MB

题目描述：
龙龙是“饱了呀”外卖软件的注册骑手，负责送帕特小区的外卖。帕特小区的构造非常特别，都是双向道路且没有构成环 —— 你可以简单地认为小区的路构成了一棵树，根结点是外卖站，树上的结点就是要送餐的地址。

每到中午 12 点，帕特小区就进入了点餐高峰。一开始，只有一两个地方点外卖，龙龙简单就送好了；但随着大数据的分析，龙龙被派了更多的单子，也就送得越来越累……

看着一大堆订单，龙龙想知道，从外卖站出发，访问所有点了外卖的地方至少一次（这样才能把外卖送到）所需的最短路程的距离到底是多少？每次新增一个点外卖的地址，他就想估算一遍整体工作量，这样他就可以搞明白新增一个地址给他带来了多少负担。

输入格式:
输入第一行是两个数 N 和 M (2 ≤ N ≤ $10^5$ , 1 ≤ M ≤ $10^5$)，分别对应树上节点的个数（包括外卖站），以及新增的送餐地址的个数。

接下来首先是一行 N 个数，第 i 个数表示第 i 个点的双亲节点的编号。节点编号从 1 到 N，外卖站的双亲编号定义为 −1。

接下来有 M 行，每行给出一个新增的送餐地点的编号 $X_i$ 。保证送餐地点中不会有外卖站，但地点有可能会重复。

为了方便计算，我们可以假设龙龙一开始一个地址的外卖都不用送，两个相邻的地点之间的路径长度统一设为 1，且从外卖站出发可以访问到所有地点。

注意：所有送餐地址可以按任意顺序访问，且完成送餐后无需返回外卖站。

输出格式:
对于每个新增的地点，在一行内输出题目需要求的最短路程的距离。

输入样例:
7 4
-1 1 1 1 2 2 3
5
6
2
4
输出样例:
2
4
4
6

给定一棵树 以及m个送餐地点

求出前 i 次的送 i 餐的最短距离总和是多少

(注： 每次送的时候外卖都是拿好的， 所以只需要求出每次最短送餐距离)

也就是我们一共要送m个外卖，一次一次来。
假设每次为 i (也就是 i=1 送前1个外卖, i = 2 送前两个外卖，以此类推）
问外卖员送前 i 个外卖最少要走几段

emmmmmmm

给个样例解释吧

样例的情况可以是这样走的

到 5

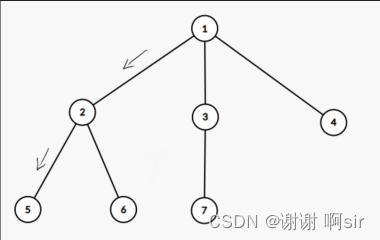
顺序 1 > 2 > 5

到 5、6

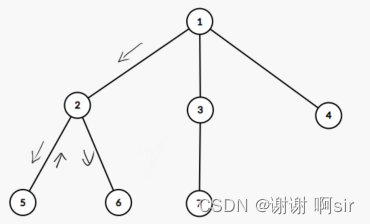
顺序 1 > 2 > 5 > 2 > 6
也可以是 1 > 2 > 6 > 2 > 5

到 5、6、2

顺序 1 > 2 > 5 > 2 > 6
也可以是 1 > 2 > 6 > 2 > 5

到 5、6、2、4

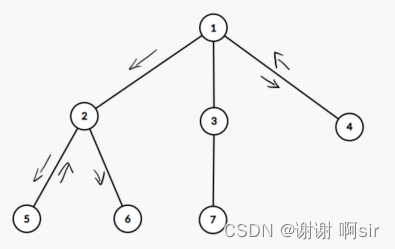
顺序 1 > 4 > 1 > 2 > 5 > 2 > 6
也可以是 1 > 4 > 1 > 2 > 6 > 2 > 5

再给一个样例

样例输入
7 3
-1 1 1 1 2 2 3
2
7
4
样例输出
1
4
6

到 2

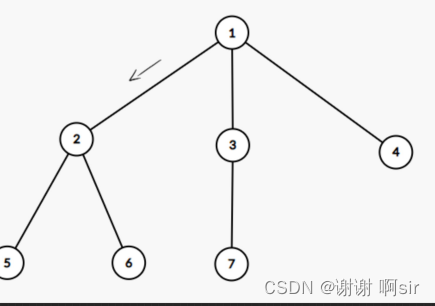
顺序 1 > 2

到 2、7

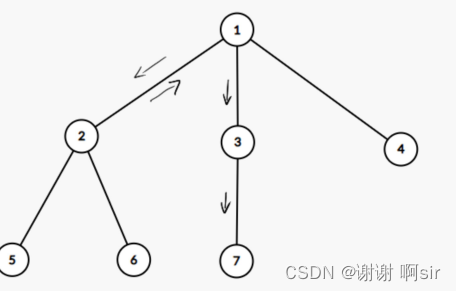
顺序 1 > 2 > 1 > 3 > 7

到 2、7、4

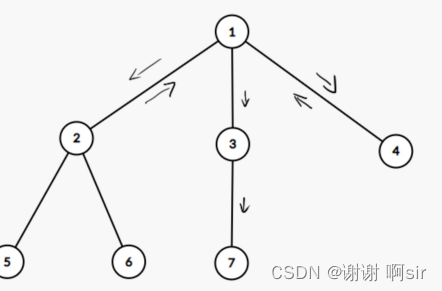
顺序 1 > 2 > 1 > 4 > 1 > 3 > 7
也可以是 1 > 4 > 1 > 2 > 1 > 3 > 7

直接看 i = 3 的情况， 如果先走到 4 然后再走到 7 的话，那么就是 6 步， 否则无论怎么走都是 7 步

可以再试着多画几个，可以推出，无论当前怎么走，只要是最后一段是走到距离根节点最远的那个节点就是最优解（如果有多个最远的相同节点，那么任选一个即可）。

有两种做法

1

可以先算出所有节点到根节点的距离

然后每一次去加上送餐点的时候
求出到最远的节点的距离 和 送完之后有多少条边

每次答案 = 边 * 2 - 到最远的节点的距离

2

每次dfs去看当前到达这个送餐点的时候 会增加多少条边
顺带着求出 根节点到最远节点的距离

每次答案 = 边 * 2 - 到最远的节点的距离

两种方法c++都可以直接过 但是java 莫名其妙的答案错误了

1

import java.io.*;
import java.math.*;
import java.util.*;public class Main
{static int N = (int) 1e5, M = N << 1;static int h[] = new int[N + 10], shu[] = new int[M + 10], ne[] = new int[M + 10], idx = 1;static int d[] = new int[N + 10];static void add(int a, int b){shu[idx] = b;ne[idx] = h[a];h[a] = idx++;}static void dfs(int u){for (int i = h[u]; i != 0; i = ne[i]){int j = shu[i];d[j] = d[u] + 1;dfs(j);}}public static void main(String[] args){int n = sc.nextInt(), m = sc.nextInt();int fa[] = new int[n + 10];int root = 0;for (int i = 1; i <= n; i++){fa[i] = sc.nextInt();if (fa[i] == -1)root = i;elseadd(fa[i], i);}dfs(root);int ans = 0, max = 0;boolean vis[] = new boolean[n + 10];while (m-- > 0){int x = sc.nextInt();max = Math.max(max, d[x]);while (x != root && !vis[x]){vis[x] = true;x = fa[x];ans++;}out.println(ans * 2 - max);}out.flush();out.close();}static Scanner sc = new Scanner(System.in);static PrintWriter out = new PrintWriter(System.out);
}

c++

#include <cstdio>
#include <algorithm>using namespace std;const int N = 1e5, M = N << 1;
int h[N + 10], shu[M + 10], ne[M + 10], idx = 1;
int fa[N + 10];
int d[N + 10];
bool vis[N + 10];void add(int a, int b)
{shu[idx] = b;ne[idx] = h[a];h[a] = idx++;
}void dfs(int u)
{for (int i = h[u]; i != 0; i = ne[i]){int j = shu[i];d[j] = d[u] + 1;dfs(j);}
}int main()
{int n, m; scanf("%d%d", &n, &m);int root = 0;for (int i = 1; i <= n; i++){scanf("%d", &fa[i]);if (fa[i] == -1)root = i;elseadd(fa[i], i);}dfs(root);int ans = 0, mx = 0;while (m-- > 0){int x; scanf("%d", &x);mx = max(mx, d[x]);while (x != root && !vis[x]){vis[x] = true;x = fa[x];ans++;}printf("%d\n", ans * 2 - mx);}return 0;
}

2

很奇怪c++能过 但是java错第四个

import java.io.*;
import java.math.*;
import java.util.*;public class Main
{static int N = (int) 1e5;static int fa[] = new int[N + 10];static int d[] = new int[N + 10];static int root = 0, max = 0;static int dfs(int u, int depth){if (u == root || d[u] != 0){max = Math.max(max, d[u] + depth);return depth * 2;}int p = dfs(fa[u], depth + 1);d[u] = d[fa[u]] + 1;return p;}public static void main(String[] args){int n = sc.nextInt(), m = sc.nextInt();for (int i = 1; i <= n; i++){fa[i] = sc.nextInt();if (fa[i] == -1)root = i;}int ans = 0;while (m-- > 0){int x = sc.nextInt();ans += dfs(x, 0);out.println(ans - max);}out.flush();out.close();}static Scanner sc = new Scanner(System.in);static PrintWriter out = new PrintWriter(System.out);
}

c++

#include <cstdio>
#include <algorithm>using namespace std;const int N = 1e5;
int fa[N + 10];
int d[N + 10];
int root = 0, mx = 0;int dfs(int u, int depth)
{if (u == root || d[u] != 0){mx = max(mx, d[u] + depth);return depth * 2;}int p = dfs(fa[u], depth + 1);d[u] = d[fa[u]] + 1;return p;
}int main()
{int n, m; scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++){scanf("%d", &fa[i]);if (fa[i] == -1)root = i;}int ans = 0;while (m-- > 0){int x; scanf("%d", &x);ans += dfs(x, 0);printf("%d\n", ans - mx);}return 0;
}

链表
链表

dfs
dfs

树的深度dfs

如果有说错的 或者 不懂的 尽管提 嘻嘻

一起进步！！！

闪现