Day60力扣打卡

本文主要是介绍Day60力扣打卡，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

打卡记录

1682分了记录下，希望下回能突破1700捏🤣🤣。作为一个菜鸟😨，知道自己不太行😭👊，从以前的周赛稳定1题到稳定2题🥺，到现在的时有时无的3题🤔，快乐捏🥰。每次刷题都期盼有所长进，虽然更多的时候收到的是遗憾🤣👉😭。最近六级 + 期末，尽量维持每日一题，等后面有空的时候再多刷刷题。😇🙏🙏

用邮票贴满网格图（二维前缀和 + 二维差分）

链接
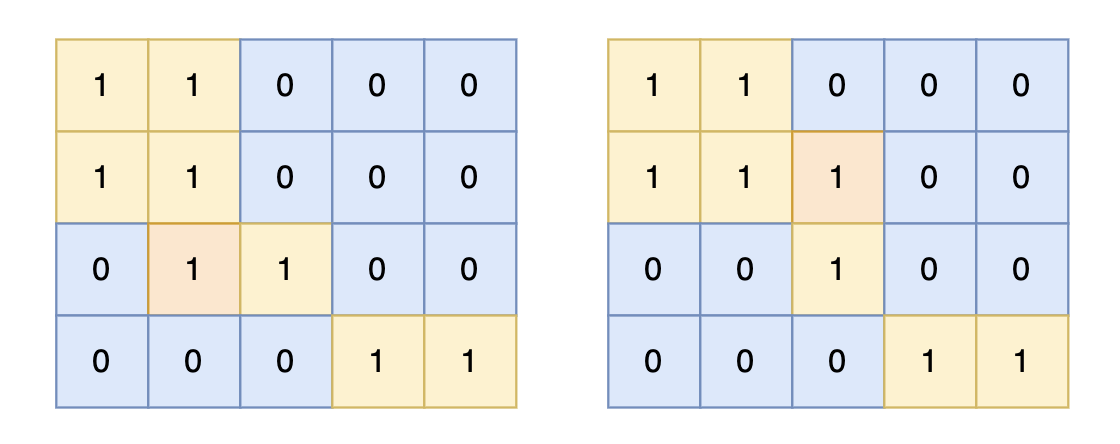
通过贪心，在能贴邮票的地方就直接贴入尽管重叠。如何判断能贴邮票的位置，通过判断枚举不同位置上的二位前缀和，若为0则邮票可以粘贴，粘贴部分用二维差分收集，最后再累加起来，得到贴完邮票的网格图，若无位置为0则可以贴满。

class Solution:def possibleToStamp(self, grid: List[List[int]], stampHeight: int, stampWidth: int) -> bool:n, m = len(grid), len(grid[0])s = [[0] * (m + 1) for _ in range(n + 1)]for i, row in enumerate(grid):for j, w in enumerate(row):s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + wd = [[0] * (m + 2) for _ in range(n + 2)]for ex in range(stampHeight, n + 1):for ey in range(stampWidth, m + 1):sx, sy = ex - stampHeight + 1, ey - stampWidth + 1if s[ex][ey] - s[sx - 1][ey] - s[ex][sy - 1] + s[sx - 1][sy - 1] == 0:d[sx][sy] += 1d[sx][ey + 1] -= 1d[ex + 1][sy] -= 1d[ex + 1][ey + 1] += 1for i, row in enumerate(grid):for j, w in enumerate(row):d[i + 1][j + 1] += d[i + 1][j] + d[i][j + 1] - d[i][j]if w == 0 and d[i + 1][j + 1] == 0:return Falsereturn True

这篇关于Day60力扣打卡的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---