本文主要是介绍Math:处理数学计算的工具,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在软件开发过程中,我们有时候需要进行些数学计算,除了简单的四则运算外,我们也许会涉及到三角函数、对数等数学应用。.Net提供了System.Math类辅助我们完成工作。
以下代码演示了Math的基本能力:
System.Console.WriteLine(System.Math.Abs(-12.01));//绝对值
System.Console.WriteLine(System.Math.PI);//圆周率
System.Console.WriteLine(System.Math.Max(12,14));//最大值
System.Console.WriteLine(System.Math.Min(12,14));//最小值
以下代码描述了Math对数据进行求接近值的不同方式:
System.Console.WriteLine(System.Math.Ceiling(12.34));//最高整数
System.Console.WriteLine(System.Math.Floor(12.34));//最低整数
System.Console.WriteLine(System.Math.Truncate(12.34));//取整
Math提供了对三角函数的处理能力:
System.Console.WriteLine(System.Math.Acos(0.45));//余弦值
System.Console.WriteLine(System.Math.Asin(0.45));//正弦值
System.Console.WriteLine(System.Math.Atan(0.45));//正切值
System.Console.WriteLine(System.Math.Sin(90));//正弦值
System.Console.WriteLine(System.Math.Sinh(90));//双曲正弦值
System.Console.WriteLine(System.Math.Tan(90));//正切值
System.Console.WriteLine(System.Math.Tanh(90));//双曲正切值
Math提供对应对数、幂等计算的方式:
System.Console.WriteLine(System.Math.Log(3, 10));//对数
System.Console.WriteLine(System.Math.Log10(3));//以 10 为底的对
System.Console.WriteLine(System.Math.Pow(2, 10));//次幂
System.Console.WriteLine(System.Math.Sqrt(9));//平方根
以下代码向我们演示了如何计算五角星每个点的位置:
int r = 50;
System.Drawing.Point[] apt = new System.Drawing.Point[5];
for (int i = 0; i < apt.Length; i++)
{
apt[i] = new System.Drawing.Point(
(int)(20 + r / 2 + Math.Sin(Math.PI * 54.0 / 180) * r *
Math.Sin(Math.PI * (i * 72.0 + 36) / 180)),
(int)(20 + r / 2 + Math.Sin(Math.PI * 54.0 / 180) * r *
Math.Cos(Math.PI * (i * 72.0 + 36) / 180)));
}
System.Drawing.Point[] aptA = new System.Drawing.Point[5];
for (int i = 0; i < aptA.Length; i++)
{
aptA[i] = new System.Drawing.Point(
(int)(20 + r / 2 + Math.Sin(Math.PI * 14.0 / 180) /
Math.Sin(Math.PI * 54.0 / 180) * r * Math.Sin(Math.PI * (i * 72.0 + 72) / 180)),
(int)(20 + r / 2 + Math.Sin(Math.PI * 14.0 / 180) /
Math.Sin(Math.PI * 54.0 / 180) * r * Math.Cos(Math.PI * (i * 72.0 + 72) / 180))
);
}
Math中最有意思的是Math.Round方法,该方法是将小数值舍入到指定精度,如果你认为这个方法是我们传统意义上的四舍五入,那你会以下代码的运行结果会非常惊讶
System.Console.WriteLine(System.Math.Round(3.25, 1));
System.Console.WriteLine(System.Math.Round(3.15, 1));
你会非常惊讶的发现运行结果并不是你所相信的3.3和3.2,而是如图3.1.16所示:
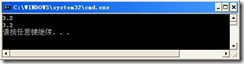
图3.1.16
原因是Round的默认精度控制是遵循 IEEE 标准 754 的第 4 节。这种舍入有时称为就近舍入或四舍六入五成双。它可以将因单方向持续舍入中点值而导致的舍入误差降到最低。说的通俗点就是,逢六必进位,逢五看奇偶,奇进偶不进。
如果我们希望精度的控制和我们目前的国内传统一致,请编写以下代码:
System.Console.WriteLine(System.Math.Round(3.25, 1, MidpointRounding.AwayFromZero));
System.Console.WriteLine(System.Math.Round(3.15, 1, MidpointRounding.AwayFromZero));
上述代码的结果则如图3.1.17所示:
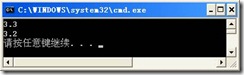
图3.1.17
这篇关于Math:处理数学计算的工具的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


