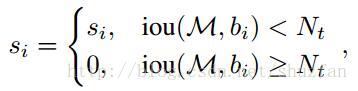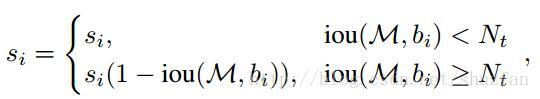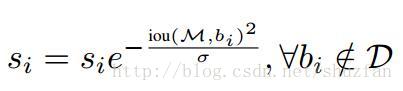一行代码改进NMS

本文主要是介绍一行代码改进NMS，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一篇讲通过改进NMS来提高检测效果的论文。

文章链接： 《Improving Object Detection With One Line of Code》

Github链接： https://github.com/bharatsingh430/soft-nms

Motivation

绝大部分目标检测方法，最后都要用到 NMS-非极大值抑制进行后处理。 通常的做法是将检测框按得分排序，然后保留得分最高的框，同时删除与该框重叠面积大于一定比例的其它框。

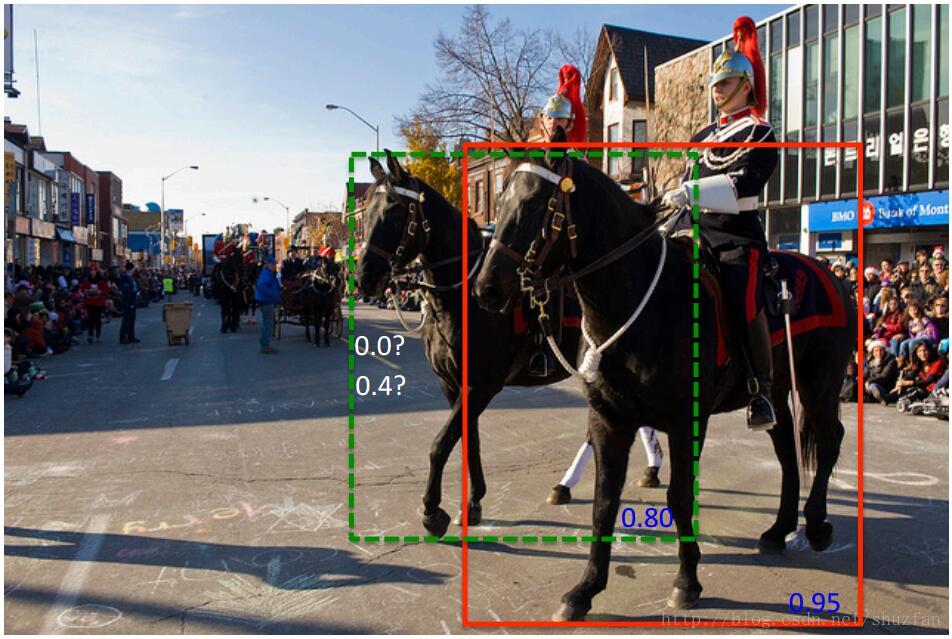
这种贪心式方法存在如下图所示的问题： 红色框和绿色框是当前的检测结果，二者的得分分别是0.95和0.80。如果按照传统的NMS进行处理，首先选中得分最高的红色框，然后绿色框就会因为与之重叠面积过大而被删掉。

另一方面，NMS的阈值也不太容易确定，设小了会出现下图的情况（绿色框因为和红色框重叠面积较大而被删掉），设置过高又容易增大误检。

思路：不要粗鲁地删除所有IOU大于阈值的框，而是降低其置信度。

Method

先直接上伪代码，如下图：如文章题目而言，就是用一行代码来替换掉原来的NMS。按照下图整个处理一遍之后，指定一个置信度阈值，然后最后得分大于该阈值的检测框得以保留

原来的NMS可以描述如下：将IOU大于阈值的窗口的得分全部置为0。

文章的改进有两种形式，一种是线性加权的：

一种是高斯加权的：

分析上面的两种改进形式，思想都是：M为当前得分最高框，\(b_i\) 为待处理框，\(b_i\) 和M的IOU越大，\(b_i\) 的得分\(s_i\) 就下降的越厉害。

具体地，下面是作者给出的代码：(当然不止一行T_T)

def cpu_soft_nms(np.ndarray[float, ndim=2] boxes, float sigma=0.5, float Nt=0.3, float threshold=0.001, unsigned int method=0):cdef unsigned int N = boxes.shape[0]cdef float iw, ih, box_areacdef float uacdef int pos = 0cdef float maxscore = 0cdef int maxpos = 0cdef float x1,x2,y1,y2,tx1,tx2,ty1,ty2,ts,area,weight,ovfor i in range(N):maxscore = boxes[i, 4]maxpos = itx1 = boxes[i,0]ty1 = boxes[i,1]tx2 = boxes[i,2]ty2 = boxes[i,3]ts = boxes[i,4]pos = i + 1# get max boxwhile pos < N:if maxscore < boxes[pos, 4]:maxscore = boxes[pos, 4]maxpos = pospos = pos + 1# add max box as a detection boxes[i,0] = boxes[maxpos,0]boxes[i,1] = boxes[maxpos,1]boxes[i,2] = boxes[maxpos,2]boxes[i,3] = boxes[maxpos,3]boxes[i,4] = boxes[maxpos,4]# swap ith box with position of max boxboxes[maxpos,0] = tx1boxes[maxpos,1] = ty1boxes[maxpos,2] = tx2boxes[maxpos,3] = ty2boxes[maxpos,4] = tstx1 = boxes[i,0]ty1 = boxes[i,1]tx2 = boxes[i,2]ty2 = boxes[i,3]ts = boxes[i,4]pos = i + 1# NMS iterations, note that N changes if detection boxes fall below thresholdwhile pos < N:x1 = boxes[pos, 0]y1 = boxes[pos, 1]x2 = boxes[pos, 2]y2 = boxes[pos, 3]s = boxes[pos, 4]area = (x2 - x1 + 1) * (y2 - y1 + 1)iw = (min(tx2, x2) - max(tx1, x1) + 1)if iw > 0:ih = (min(ty2, y2) - max(ty1, y1) + 1)if ih > 0:ua = float((tx2 - tx1 + 1) * (ty2 - ty1 + 1) + area - iw * ih)ov = iw * ih / ua #iou between max box and detection boxif method == 1: # linearif ov > Nt: weight = 1 - ovelse:weight = 1elif method == 2: # gaussianweight = np.exp(-(ov * ov)/sigma)else: # original NMSif ov > Nt: weight = 0else:weight = 1boxes[pos, 4] = weight*boxes[pos, 4]# if box score falls below threshold, discard the box by swapping with last box# update Nif boxes[pos, 4] < threshold:boxes[pos,0] = boxes[N-1, 0]boxes[pos,1] = boxes[N-1, 1]boxes[pos,2] = boxes[N-1, 2]boxes[pos,3] = boxes[N-1, 3]boxes[pos,4] = boxes[N-1, 4]N = N - 1pos = pos - 1pos = pos + 1keep = [i for i in range(N)]return keep

Experiments

下图可以看出，基本可以获得平均1%的提升，且不增加额外的训练和计算负担。

高斯方差以及NMS的IOU阈值的敏感性测试：

这篇关于一行代码改进NMS的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---