本文主要是介绍Beyond triplet loss—— Re-ID,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一篇讲Person Re-ID的论文,来自CVPR2017,同样是改进了Triplet Loss。
文章链接: 《Beyond triplet loss: a deep quadruplet network for person re-identification》
Introduction
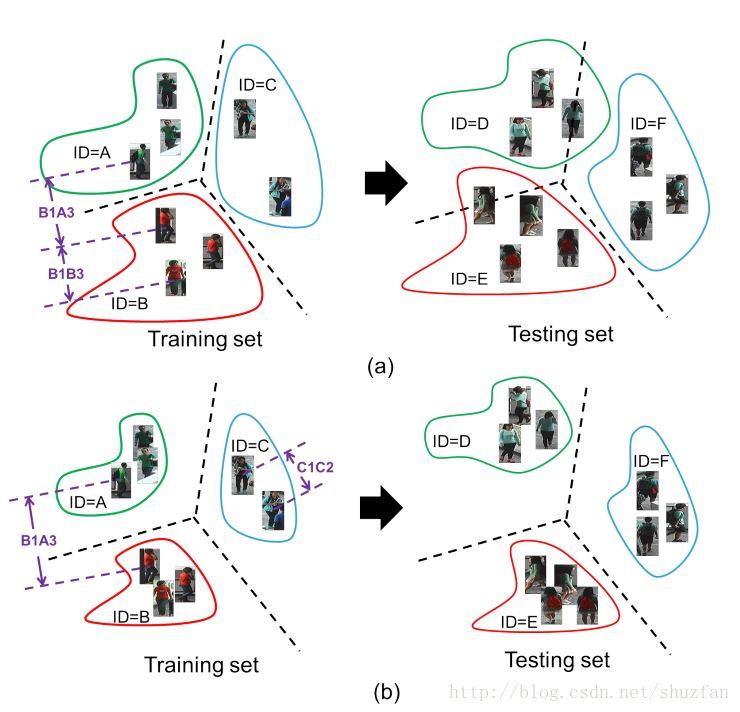
文章的出发点就在上面这张图。 如上图a,传统的Triplet Loss可能在test集上泛化效果一般,主要是因为类内方差依然比较大。文章对此增加了新的约束,用于 减小类内方差 和 增加类间方差。
即,新的Loss不仅要求 \(B_1B_3< B_1A_3\) 同时要求 \(C_1C_2< B_1A_3\)。
减小类内方差 和 增加类间方差 这一经典思想早期主要流行在线性判别分析(LDA)上。 Deep Learning时代,DeepLDA(参考文献[1])将这一思想继续发扬光大,不过好像训练难度比较大。 ImpTrpLoss(参考文献[2]) 同样考虑到进一步约束类内误差,他们在Triplet Loss的基础上进一步约束属于同类的pair的距离应当小于一个预设值。
Method
首先是传统的Triplet Loss,如下式: \(x_i\) 、 \(x_j\)属于同一类,\(x_k\)属于另一类,\(\alpha_{trp}\) 表示预设的margin, \(f(x_i)\)表示归一化的高度嵌入的特征。 其描述的网络结构如上图a所示。
上式直接使用欧式距离作为相似性度量,作者准备用一种可以学习的方式来代替,于是就有了下式: \(g(x_i,x_j)\)表示一种新的相似性测度,其描述的网络结构如上图b所示。
上式中的\(g(x_i,x_j)\)还有必要约束一下范围,否则会造成学习很不稳定。(比如要求 \(g_1-g_2<0.1\), 如果\(g\)不约束范围,那么\(g_1 和g_2\) 同时放大10000倍将会使得约束阈值毫无意义。)于是作者在后面增加了一个Softmax约束来获得
[0,1]的相似度,同时作者也增加了一个softmax loss,整体网络结构如上图c所示。
在上面的基础上,作者完善了自己的Quadruplet Loss:
上式共有两项,前一项是传统的Triplet Loss,后一项用于进一步缩小类内差距。 由于前一项的重要更大,因此作者控制 \(\alpha_1 > \alpha_2\).
另一方面,如何确定margin的值也是一件让人很头疼的事情,选择小了收敛不好,选择大了不好收敛。 文章为此采用了一种自适应margin设定策略:
即margin设定为同类距离均值与异类距离均值之差,w用来调整大小,具体地对于\(\alpha_1\),\(w=1\);对于\(\alpha_2\),\(w=0.5\)。
训练初期,上面的margin策略可能导致难以收敛,因此作者前期先使用固定的margin,稳定后再实行该策略。
具体训练时,作者采用了如下图所示的四元组:
评价
实验部分就不分析了。 最近改进Triplet Loss来做Re-ID的很多,虽然各各都声称效果不错,但实际上也都没有特别明显的提高。 同时,很多文章里面的一些结论或者说经验都有相互冲突的地方。因此,我还是比较欣赏那个说法:
我只能保证我的方法在这个任务上比较好,对于其它任务,还需要实际的检验。
参考文献
[1] L. Wu, C. Shen, and A. van den Hengel. Deep linear discriminant analysis on fisher networks: A hybrid architecture for person re-identification. Pattern Recognition, 2016
[2] D. Cheng, Y. Gong, S. Zhou, J. Wang, and N. Zheng. Person re-identification by multi-channel parts-based cnn with improved triplet loss function. In CVPR, 2016
这篇关于Beyond triplet loss—— Re-ID的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!