自编码器 AutoEncoder

本文主要是介绍自编码器 AutoEncoder，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

自编码器（AutoEncoder），也称自编码模型，是一种基于无监督学习的数据维度压缩和特征表示方法，目的是对一组数据学习出一种表示。1986年 Rumelhart 提出自编码模型用于高维复杂数据的降维。由于自动编码器通常应用于无监督学习，所以不需要对训练样本进行标记。自动编码器在图像重构、聚类、降维、自然语言翻译等方面应用广泛。

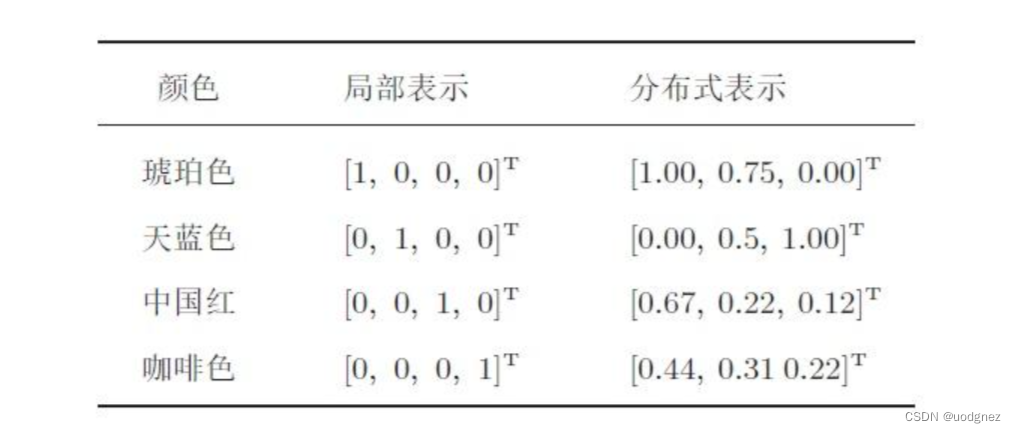
1. 数据表示

数据表示（Data Representation）是使用另一种形式呈现原始数据的方法，这一技术也被称为隐式表示（Latent Representation）或者转码（Coding）。

• 原始数据为 $[2,4,6,8,10]$：
  我们可以使用文字以2开头，以10结尾的偶数列来表示该原始数据，也可以使用 $[x,2x,3x,4x,5x]$ 且 $x=2$ 来表示该原始数据。
• 原始数据为 ${[}^{\prime }苹{果}^{\prime }{,}^{\prime }{梨}^{\prime }{,}^{\prime }百香{果}^{\prime }]$：
  我们可以使用序列 $[0,1,2]$ 来表示该原始数据，也可以使用水果这一概括性的词汇来表示原始数据。

很显然，一个数据的数据表示并不是唯一的，且这种表示可以是精确的、也可以是有些模糊的，甚至可以看起来与原始数据毫不相关，但无论如何，数据表示的结果必须携带原始数据上大部分的信息。广义地表示，只要数据B是以另一种形式呈现数据A、并且数据B上携带数据A大部分的信息，我们就可以说B是A的数据表示。同时，“另一种形式”既可以是文字-数字这样不同类别的数据之间的形式差异，也可以是数字-数字这样相同类别，但不同大小、不同数量的数据之间的形式差异。在实际计算当中，当数据B是数据A的数据表示时，数据B通常是从数据A总结出的规律、或直接在数据A上计算得出的新数据。

根据以上数据表示的广义定义可以得知，我们非常熟悉的数据编码（独热编码、顺序编码等操作）、特征提取、升维降维、Embedding等方法都可以囊括到数据表示领域当中。在这领域当中，使用机器学习或深度学习手段令算法自己求解出数据表示结果的领域被称之为表征学习。自编码器是表征学习中极具特色的代表架构。为了实现数据表示的功能，自编码器能够“接收数据A，并输出另一种形式的数据B”，因此自编码器是为“生产新数据”而生的架构。

2. 自编码器模型简介

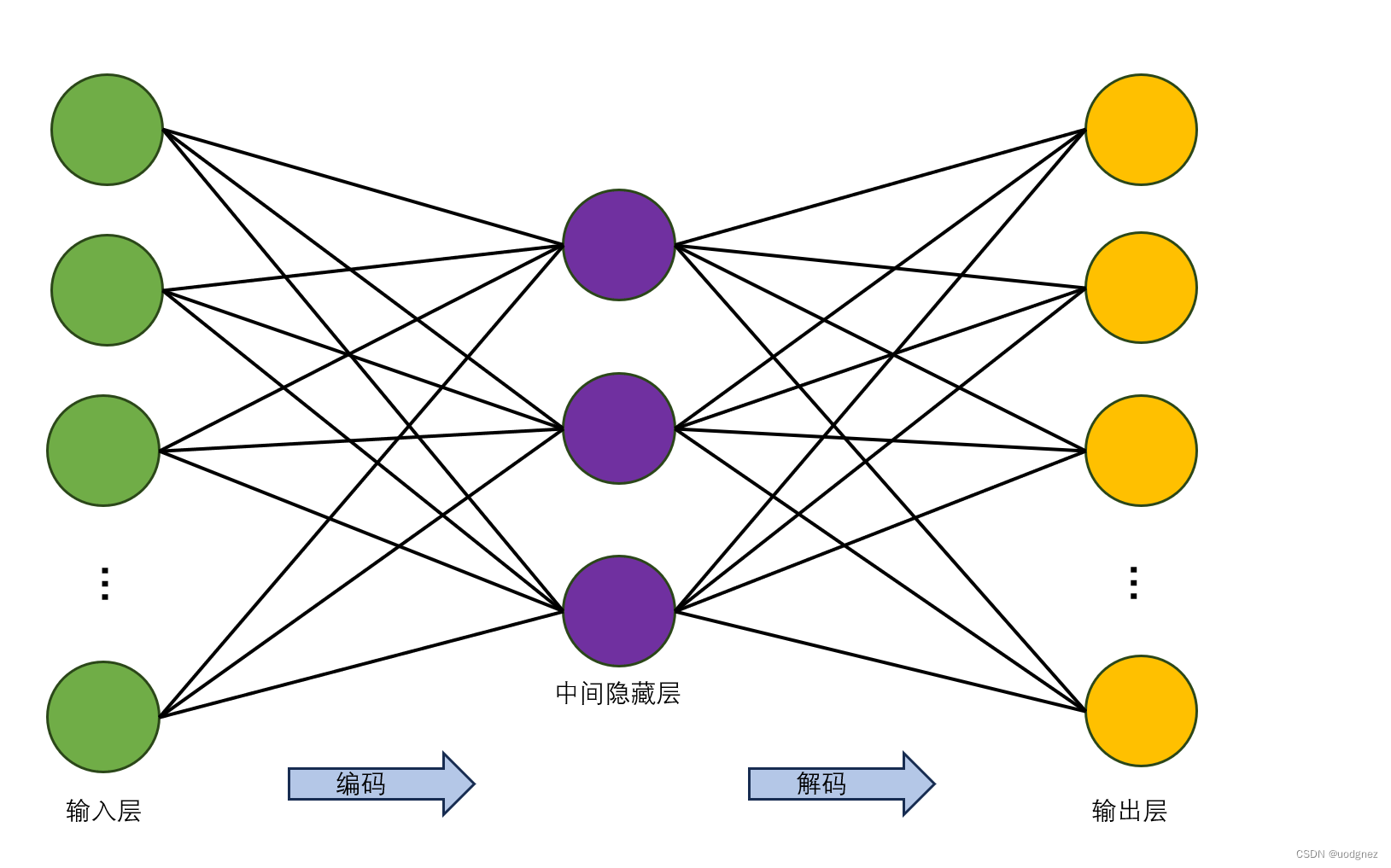
最初的自编码器是一个三层网络结构，即输入层、中间隐藏层以及输出层，其中输入层和输出层的神经元个数相同。如下图所示：

深度自编码器是将自编码器堆积起来，可以包含多个中间隐藏层。由于其可以有更多的中间隐藏层，所以对数据的表示和编码能力更强，而且在实际应用中也更加常用。如下图所示：

稀疏自编码器，是在原有自编码器的基础上，对隐层单元施加稀疏性约束，这样会得到对输入数据更加紧凑的表示，在网络中仅有小部分神经元会被激活。常用的稀疏约束是使用 $\text{L1}$ 范数约束，目的是让不重要的神经元的权重为0。

卷积自编码器是使用卷积层搭建获得的自编码网络。当输入数据为图像时，由于卷积操作可以从图像数据中获取更丰富的信息，所以使用卷积层作为自编码器隐藏层，通常可以对图像数据进行更好的表示。在实际应用中，用于处理图像的自动编码器的隐藏层几乎都是基于卷积的自编码器。在卷积自编码器的编码器部分，通常可以通过池化层负责对数据进行下采样，卷积层负责对数据进行表示，而解码器则通常使用可以对特征映射进行上采样的操作来完成。

这篇关于自编码器 AutoEncoder的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---