本文主要是介绍U2 文法和语言,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 一、预备知识
- 1、字母表和符号串
- 2、符号串形式定义
- 3、符号串相等
- 4、延申
- 二、文法
- 1、 一些概念
- 2、文法的定义
- 3、推导的形式定义
- 4、规范推导
- 5、语言的形式定义
- 6、递归文法
- 7、BNF范式
- 总结
- 三、短语、简单短语和句柄
- 四、语法树(推导树)
- 1、概念
- 2、语法树推导--句型的推导
- 3、规约
- 五、二义性
- 1、二义性文法
- 2、二义性的改进
- 3、有害文法
- 六、乔姆斯基文法体系
- 1、概念
- 2、分类
一、预备知识
1、字母表和符号串
字母表: 符号的非空有限集 例: ∑ \sum ∑= a , b , c {a,b,c} a,b,c
符号: 字母表中的元素 例: a , b , c a,b,c a,b,c
符号串: 符号的有穷序列 例: a , a a , a c , a b c , . . a, aa, ac, abc,.. a,aa,ac,abc,..
空符号串:无任何符号的符号串 ( ε ) (ε) (ε)
2、符号串形式定义
有字母表 ∑ \sum ∑,定义:
(1)ε是 ∑ \sum ∑上的符号串;
(2)若x是 ∑ \sum ∑上的符号串,且a ∈ \in ∈ ∑ \sum ∑,则 ax 或 xa 是 ∑ \sum ∑上的符号串;
(3)y是 ∑ \sum ∑上的符号串, i f f iff iff (当且仅当)y可由(1)和(2)产生。
3、符号串相等
- 符号串相等:若x、y是集合上的两个符号串,则x=y iff(当且仅当)组成x的每一个符号和组成y的每一个符号依次相等
- 符号串的长度:x为符号串,其长度 ∣ x ∣ |x| ∣x∣等于组成该符号串的符号个数。
- 符号串的联接:若x、y是定义在Σ上的符号串, 且 x = X Y , y = Y X x=XY,y=YX x=XY,y=YX,则x和y的联接 x y = X Y Y X xy=XYYX xy=XYYX也是 Σ Σ Σ上的符号串。
- 符号串集合的乘积运算:令A、B为符号串集合,定义 A B = AB= AB={ x y ∣ x ∈ A , y ∈ B xy |x∈A, y∈B xy∣x∈A,y∈B}
A = A= A={ s , t s, t s,t}, B = B = B= { u , v u,v u,v}, A B = AB= AB={ s u , s v , t u , t v su,sv,tu,tv su,sv,tu,tv}
注意因为 ε x = x ε = x εx=xε=x εx=xε=x,所以{ ε ε ε} A = A A=A A=A { ε ε ε} = A =A =A。但 ε A εA εA= A ε Aε Aε= ∅ ∅ ∅ - 符号串集合的幂运算: A 2 A^2 A2=AA , A n = A n − 1 A = A A n − 1 A^n=A^{n-1}A=AA^{n-1} An=An−1A=AAn−1
- 符号串集合的闭包运算:设A是符号串集合,定义
A + = A 1 ∪ A 2 ∪ A 3 ∪ … … ∪ A n ∪ … A^+= A^1 ∪ A^2 ∪ A^3 ∪……∪ A^n ∪… A+=A1∪A2∪A3∪……∪An∪… 称为集合A的正闭包。
A ∗ = A 0 ∪ A + A*= A^0 ∪A^+ A∗=A0∪A+ 称为集合A的闭包
4、延申
- 若A为某语言的基本字符集( 把字符看作符号)
A = A= A={ a , b , … … z , 0 , 1 , … … , 9 , + , - , × , , / , ( , ) , = , … … a, b, ……z, 0, 1, ……, 9, +, -, ×, _, /, ( , ), =, …… a,b,……z,0,1,……,9,+,-,×,,/,(,),=,……} - B为单词集 (单词是符号串)
B = B = B={ b e g i n , e n d , i f , t h e n , e l s e , f o r , … … , < 标识符 > , < 常量 > , … … begin, end, if, then, else, for, ……,<标识符>,<常量>, …… begin,end,if,then,else,for,……,<标识符>,<常量>,……} - C是句子(语言的句子是定义在B上的符号串。)
若令C为句子集合,则 C ⊂ B ∗ C \subset B* C⊂B∗ , 程序 ⊂ C \subset C ⊂C - 词法:若把字符看作符号,则单词就是符号串,单词集合就是符号串的集合。
- 句法:若把单词看作符号,则句子就是符号串,而所有句子的集合(即语言)就是符号串的集合。
二、文法
1、 一些概念
- 文法:对语言结构的定义与描述。即从形式上用于描述和规定语言结构的称为“文法”(或称为“语法”)。
- 语法规则:我们通过建立一组规则,来描述句子的语法结构。规定用“ : : = ::= ::=”表示“由…组成”(或“定义为…”)。 eg. < 句子 > : : = < 主语 > < 谓语 > <句子>::=<主语><谓语> <句子>::=<主语><谓语>
- 由规则推导句子:有了一组规则之后,可以按照一定的方式用它们去推导或产生句子。
- 推导方法:从一个要识别的符号开始推导,即用相应规则的右部来替代规则的左部,每次仅用一条规则去进行推导。
这种推导一直进行下去,直到所有带< >的符号都由终结符号替代为止
有若干语法成分同时存在时,我们总是从最左的语法成分进行推导,这称之为最左推导,类似的有最右推导(还有一般推导)。
从一组语法规则可推出不同的句子,如以上规则还可推出“大象吃象”、“大花生吃象”、“大花生吃花生”等句子,它们 在语法上都正确,但在语义上都不正确。
所谓文法是在形式上对句子结构的定义与描述,而未涉及语义问题。
5. 语法(推导)树:我们用语法(推导)树 来描述一个句子的语法结构。
语法成分:在形式语言中又称“非终结符”
单词符号:在形式语言中又称“终结符号”
2、文法的定义
文法 G = ( V n , V t , P , Z ) 文法G=(V_n,V_t,P,Z) 文法G=(Vn,Vt,P,Z)
V n :非终结符号集 V_n:非终结符号集 Vn:非终结符号集
V t :终结符号集 V_t:终结符号集 Vt:终结符号集
P :产生式或规则的集合 P:产生式或规则的集合 P:产生式或规则的集合
Z :开始符号(识别符号) Z ∈ V n Z:开始符号(识别符号) Z∈Vn Z:开始符号(识别符号)Z∈Vn
其中, V = V n ∪ V t V=V_n ∪V_t V=Vn∪Vt称为文法的字汇表。
规则: U : : = x U ∈ V n , x ∈ V ∗ 规则:U ::= x \ \ \ \ U ∈V_n, x∈V^* 规则:U::=x U∈Vn,x∈V∗
规则的定义:规则是一个有序对(U, x), 通常写为: U : : = x U ::= x U::=x 或 U → x U → x U→x , ∣ U ∣ = 1 | U| = 1 ∣U∣=1 ∣ x ∣ |x| ∣x∣ >= 0 0 0
3、推导的形式定义
文法 G : v = x U y , w = x u y 文法G:v=xUy,w=xuy 文法G:v=xUy,w=xuy
其中 x 、 y ∈ V ∗ , U ∈ V n , u ∈ V ∗ 其中x、y ∈V^*,U∈V_n , u ∈V^* 其中x、y∈V∗,U∈Vn,u∈V∗
若 U : : = u ∈ P ,则 v = > G w 若U ::= u∈P,则v =>^G w 若U::=u∈P,则v=>Gw
若 x = y = ε 有 U : : = u ,则 U = > G u 若x=y=ε \ \ 有U ::= u,则U =>^G u 若x=y=ε 有U::=u,则U=>Gu
文法 G , u 0 , u 1 , u 2 , … … , u n ∈ V + 文法G,u_0, u_1, u_2, ……,u_n∈V^+ 文法G,u0,u1,u2,……,un∈V+
i f v = u 0 = > G u 1 = > G u 2 = > G … … = > G u n = w if \ \ \ v= u_0=>^G u_1=>^G u_2 =>^G…… =>^G u_n=w if v=u0=>Gu1=>Gu2=>G……=>Gun=w
则 v = > G + w 则 v =>_G^+w 则v=>G+w
文法 G ,有 v , w ∈ V + 文法G,有v,w ∈V^+ 文法G,有v,w∈V+
i f v = > G + w , 或 v = w ,则 v = > G ∗ w if v =>_G^+w , 或v=w,则 v =>_G^*w ifv=>G+w,或v=w,则v=>G∗w
4、规范推导
有 x U y = = > x u y , 若 y ∈ V t ∗ , 则此推导为规范的,记为 x U y 有xUy ==> xuy, 若 y ∈V_t^* , 则此推导为规范的,记为 xUy 有xUy==>xuy,若y∈Vt∗,则此推导为规范的,记为xUy =|=> x u y xuy xuy
直观意义:规范推导=最右推导
最右推导:若规则右端符号串中有两个以上的非终结符时,先推右边的。
最左推导:若规则右端符号串中有两个以上的非终结符时,先推左边的
若有v = u0 =|=> u1=|=> u2=|=>……=|=> un= w, 则 v v v = ∣ = > + =|=>^+ =∣=>+ w w w
5、语言的形式定义
- 句型: x 是句型 等价于 Z = > ∗ x , 且 x ∈ V ∗ ; 句型:x是句型\ \ \ 等价于\ \ \ Z =>^* x , 且 x∈V^* ; 句型:x是句型 等价于 Z=>∗x,且x∈V∗;
- 句子: x 是句型 等价于 Z = > + x , 且 x ∈ V t ∗ ; 句子:x是句型\ \ \ 等价于\ \ \ Z =>^+ x , 且 x∈V_t^* ; 句子:x是句型 等价于 Z=>+x,且x∈Vt∗;
- 语言: L ( G [ Z ] ) = 语言:L(G[Z])= 语言:L(G[Z])={ x ∣ x ∈ V t ∗ , Z = > + x x | x∈V_t^*, Z =>^+ x x∣x∈Vt∗,Z=>+x} ;
G 和 G ’是两个不同的文法,若 L ( G ) = L ( G ’ ) , 则 G 和 G ’为等价文法。 G和G’是两个不同的文法,若 L(G) = L(G’) ,则G和G’为等价文法。 G和G’是两个不同的文法,若L(G)=L(G’),则G和G’为等价文法。
6、递归文法
递归规则:规则右部有与左部相同的符号(非终结符)对于 U : : = x U y U::= xUy U::=xUy
- 若 x = ε , 即 U : : = U y ,左递归 若x=ε, 即U::= Uy, 左递归 若x=ε,即U::=Uy,左递归
- 若 y = ε , 即 U : : = x U ,右递归 若y=ε, 即U::= xU, 右递归 若y=ε,即U::=xU,右递归
- 若 x , y ≠ ε ,即 U : : = x U y ,自嵌入递归 若x, y≠ε,即U::= xUy,自嵌入递归 若x,y=ε,即U::=xUy,自嵌入递归
递归文法:文法G,存在 U ∈ V n U ∈V_n U∈Vn
i f U = = > + … U … , 则 G 为递归文法; if \ \ U==>^+…U…, 则G为递归文法; if U==>+…U…,则G为递归文法;
i f U = = > U + … , 则 G 为左递归文法; if\ \ U==>U^+…, 则G为左递归文法; if U==>U+…,则G为左递归文法;
i f U = = > + … U , 则 G 为右递归文法。 if\ \ U==>^+…U, 则G为右递归文法。 if U==>+…U,则G为右递归文法。
递归文法的优点:可用有穷条规则,定义无穷语言
左递归文法的缺点:不能用自顶向下的方法来进行语法分析
7、BNF范式
巴克斯范式(Backus-Naur Form,简称BNF)是一种用于描述上下文无关文法(Context-Free Grammar,简称CFG)的形式化表示方法,具体规则如下:
- 非终结符(Non-terminal symbols):用尖括号括起来,表示语法规则的左侧。非终结符表示一类语法结构,可以根据产生式规则进行替换。
- 终结符(Terminal symbols):用引号括起来,表示语法规则的右侧。终结符是构成实际句子的基本符号,是语言中的实际词汇或符号。
expr -> expr '+' term | expr '-' term | term
term -> term '*' factor | term '/' factor | factor
factor -> '(' expr ')' | NUMBER
总结
编译主要的目的是: 给定 C 语言程序 x 以及语言规范 G , 求 x ∈ L ( G ) ? 给定C语言程序 x 以及语言规范 G , 求x ∈L(G) ? 给定C语言程序x以及语言规范G,求x∈L(G)?
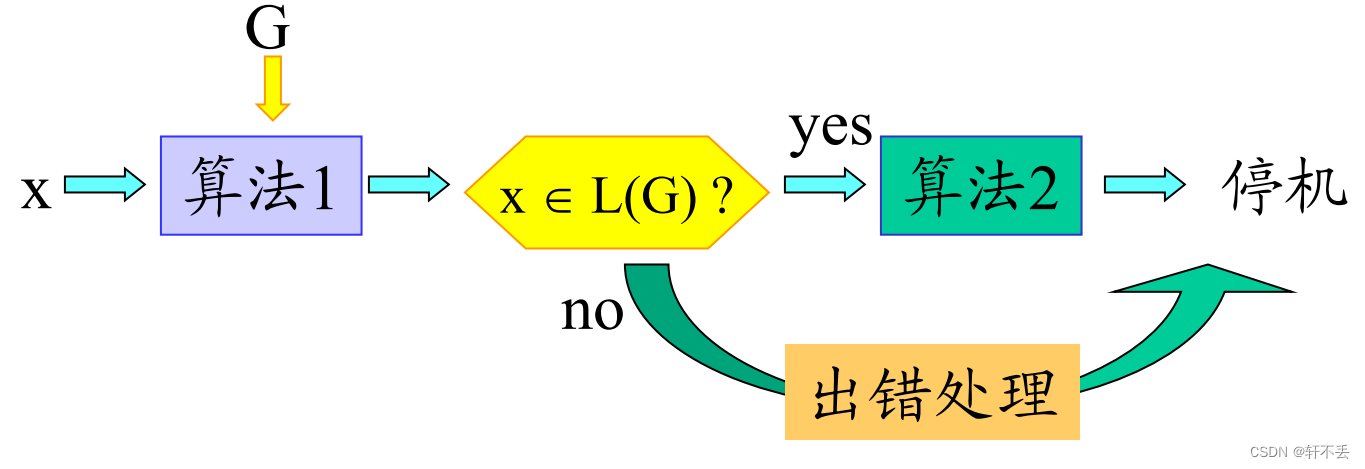
三、短语、简单短语和句柄
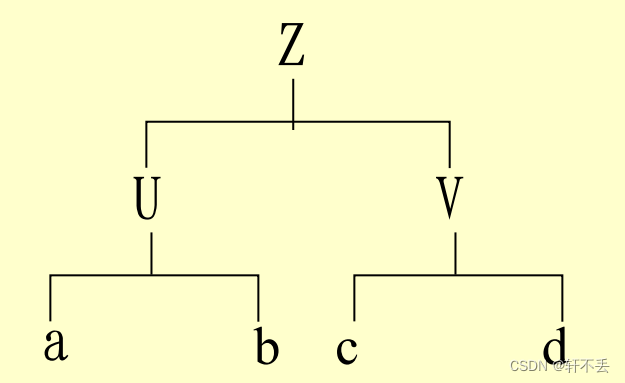
给定文法 G [ Z ] , w = x u y ∈ V + ,为该文法的句型 给定文法G[Z], w = xuy∈V+,为该文法的句型 给定文法G[Z],w=xuy∈V+,为该文法的句型
若 Z = = > ∗ x U y , 且 U = = > + u , 则 u 是句型 w 相对于 U 的 若 Z ==>^* xUy, 且U ==>^+u, 则u是句型w相对于U的 若Z==>∗xUy,且U==>+u,则u是句型w相对于U的短语;
若 Z = = > ∗ x U y , 且 U = = > u , 则 u 是句型 w 相对于 U 的 若 Z ==>^* xUy, 且U ==>u, 则u是句型w相对于U的 若Z==>∗xUy,且U==>u,则u是句型w相对于U的简单短语。
其中 U ∈ V n , u ∈ V + , x , y ∈ V ∗ 其中U ∈V_n,u ∈V^+,x , y ∈V^* 其中U∈Vn,u∈V+,x,y∈V∗
任一句型的最左简单短语称为该句型的 任一句型的最左简单短语称为该句型的 任一句型的最左简单短语称为该句型的句柄。

直观理解:短语u 是目标句型w的一部分或全部,是推导过程的前面某个句型(xUy)中的某个非终结符(U)所能推出的符号串。
任何句型本身一定是相对于识别符号Z的短语
四、语法树(推导树)
1、概念
句子( 句型)结构的图示表示法,它是有向图,由结点和有向边组成。
根结点: 识别符号(非终结符)。
中间结点:非终结符。
叶结点: 终结符或非终结符。
有向边:表示结点间的派生关系。
2、语法树推导–句型的推导
一般采用自顶向下分析法
给定G[Z],句型w:可建立推导序列, Z = = > G ∗ w Z ==>_G^* w Z==>G∗w
可建立语法树,以Z为树根结点,每步推导生成语法树的一枝,最终可生成句型w的语法树。
3、规约
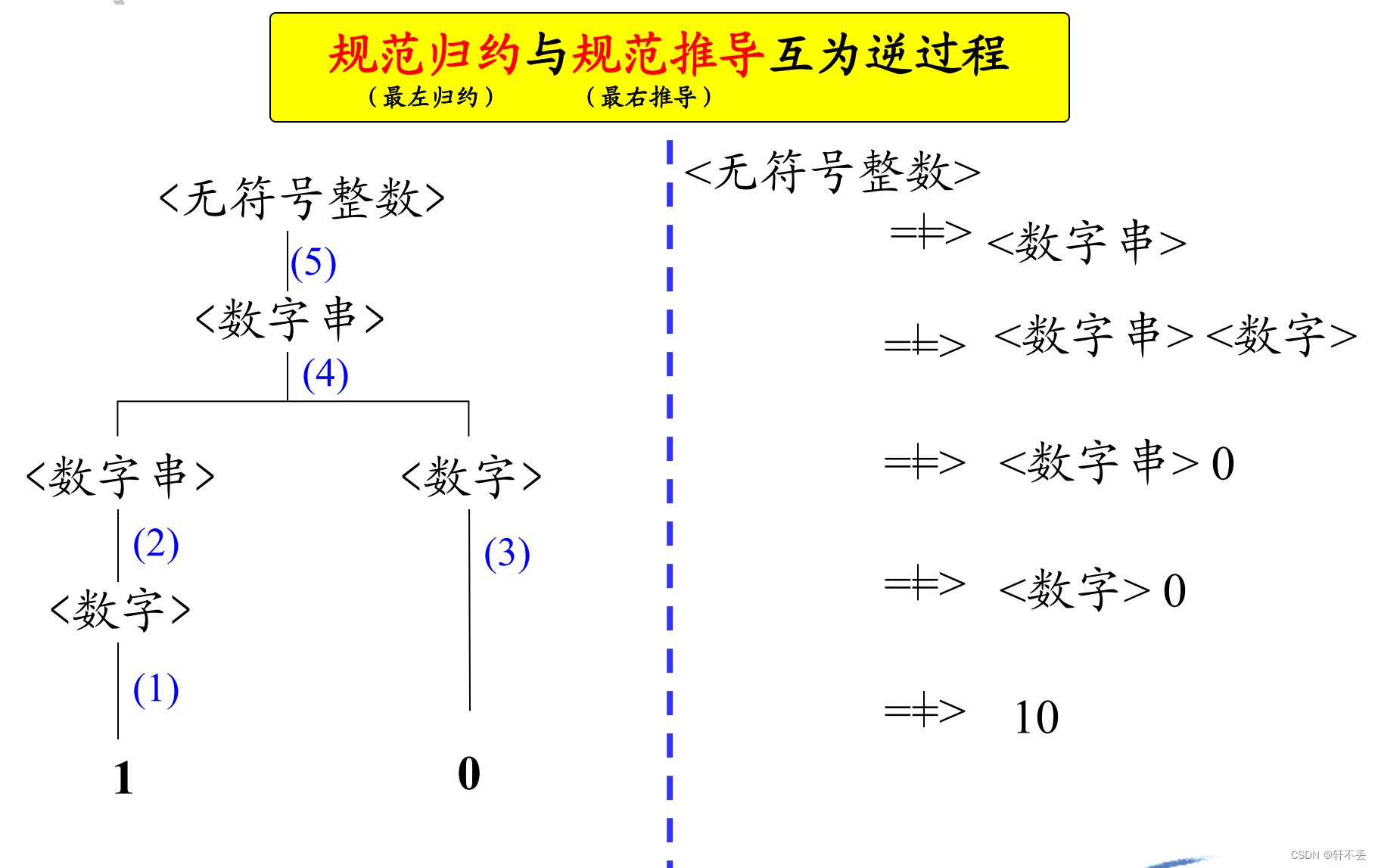
自下而上地修剪子树的某些末端结点(短语),直至把整棵树剪掉(留根),每剪一次对应一次归约。
从句型开始,自右向左地逐步进行归约,建立推导序列。
通常我们每次都剪掉当前句型的句柄(最左简单短语)即每次均进行规范归约。即对句型中最左简单短语(句柄) 进行的归约称为 规范归约
五、二义性
1、二义性文法
若对于一个文法的某一句子(或句型)存在两棵不同的语法树,则该文法是二义性文法,否则是无二义性文法。
无二义性文法的句子只有一棵语法树,尽管推导过程可以不同。(如最左推导,规范推导等)
若一个文法的某句子存在两个不同的规范推导,则该文法是二义性的,否则是无二义性的。
若文法是二义性的,则在编译时就会产生不确定性,遗憾的是在理论上已经证明:文法的二义性是不可判定的,即不可能构造出一个算法,通过有限步骤来判定任一文法是否有二义性。
现在的解决办法是:提出一些限制条件,称为无二义性的充分条件,当文法满足这些条件时,就可以判定文法是无二义性的。
2、二义性的改进
优先级的实现:层次定义:越靠上层,优先级越低;越靠下层,优先级越高

3、有害文法
- 若文法中有如U::=U的规则,则这就是有害规则,它会引起二义性

- 多余规则:在推导文法的所有句子中,始终用不到的规则。即该规则的左部非终结符不出现在任何句型中(不可达符号)
在推导句子的过程中,一旦使用了该规则,将推不出任何终结符号串。即该规则中含有推不出任何终结符号串的非终结符(不活动符号)
六、乔姆斯基文法体系
1、概念
形式语言:用文法和自动机所描述的没有语义的语言。
文法定义:乔姆斯基将所有文法都定义为一个四元组:
文法 G = ( V n , V t , P , Z ) 文法G=(V_n,V_t,P,Z) 文法G=(Vn,Vt,P,Z)
V n :非终结符号集 V_n:非终结符号集 Vn:非终结符号集
V t :终结符号集 V_t:终结符号集 Vt:终结符号集
P :产生式或规则的集合 P:产生式或规则的集合 P:产生式或规则的集合
Z :开始符号(识别符号) Z ∈ V n Z:开始符号(识别符号) Z∈Vn Z:开始符号(识别符号)Z∈Vn
2、分类
文法和语言分类:0型、1型、2型、3型
这几类文法的差别在于对产生式(语法规则)施加不同的限制。
- 0型——PSG
P : u : : = v 其中 u ∈ V + , v ∈ V ∗ V = V n ∪ V t P: u ::= v其中 u∈V^+,v∈V^* \ \ \ V = V_n∪ V_t P:u::=v其中u∈V+,v∈V∗ V=Vn∪Vt
0型文法称为短语结构文法。规则的左部和右部都可以是符号串,一个短语可以产生另一个短语 - 1型——CSG(上下文有关文法)
P : x U y : : = x u y 其中 U ∈ V n , x 、 y 、 u ∈ V ∗ P: xUy ::= xuy\ \ 其中 U∈V_n, x、y、u∈V^* P:xUy::=xuy 其中U∈Vn,x、y、u∈V∗
称为上下文敏感或上下文有关。也即只有在x、y这样的上下文中才能把U改写为u。
左边即要有多个终结符或者非终结符,一定要有终结符。
1型和0型区别是左边与右边长度比较,1型右边一定比左边长 - 2型——CFG(上下文无关文法)
P : U : : = u 其中 U ∈ V n , u ∈ V ∗ P: U ::= u其中 U∈V_n, u∈V^* P:U::=u其中U∈Vn,u∈V∗
称为上下文无关文法。也即把U改写为u时,不必考虑上下文。(1型文法的规则中x,y均为 ε 时即为2型文法)
箭头左边一般一个字符,因此推导不受上下文约束
2型文法与BNF表示相等价 - 3型——RG(正则文法)

3型文法称为正则文法。它是对2型文法进行进一步限制,一个规则中只允许一个终结符和一个非终结符组合。
3、总结
二义性和这些文法的关系
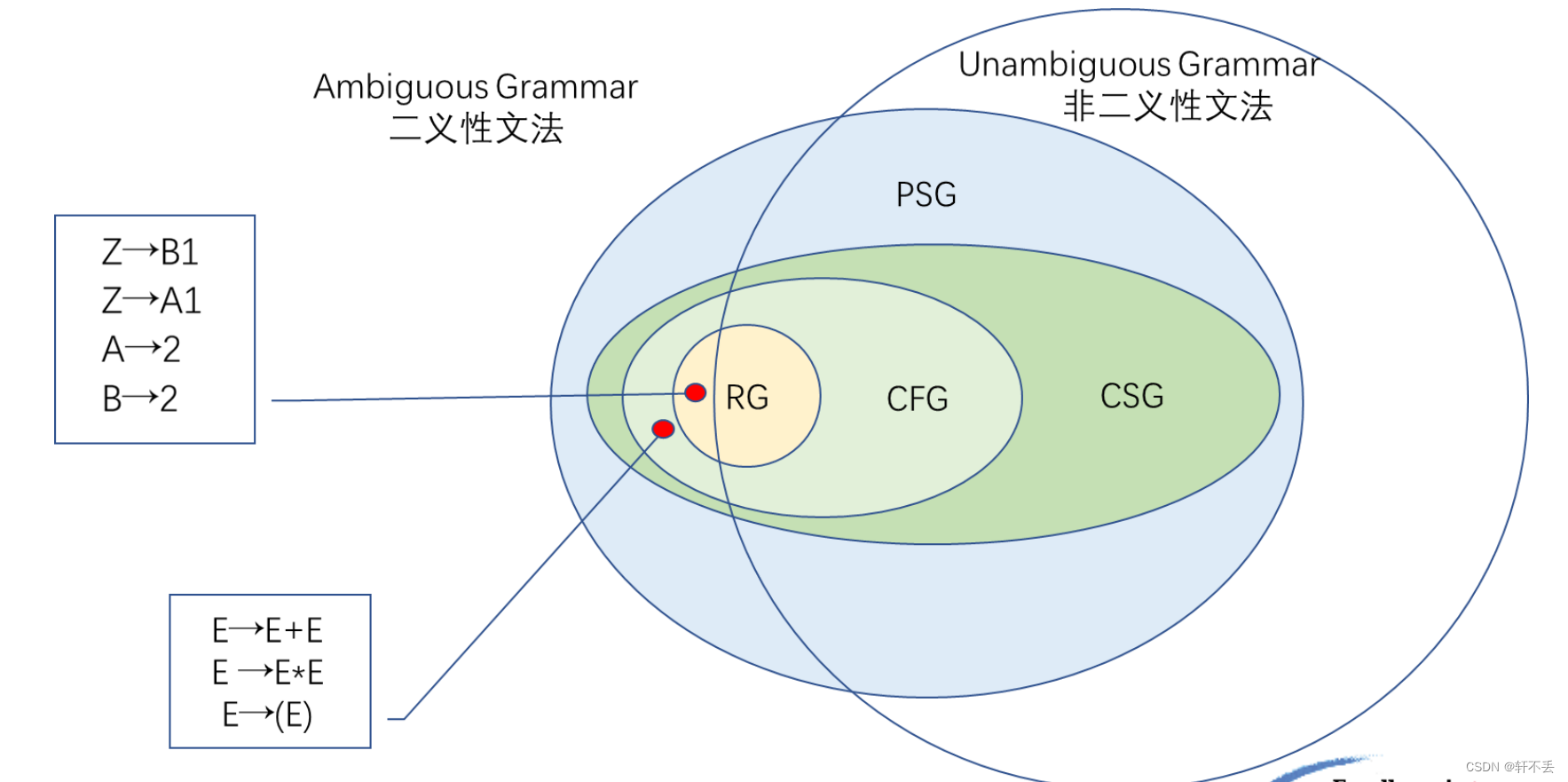
这篇关于U2 文法和语言的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






