Nested Dfs算法——判断Büchi自动机接受语言是否为空

前言

本文是写给学生看的系统分析与验证笔记（十二）——验证ω-正则属性的代码实现篇，因为想把课程笔记与自己的实现代码分离，所以就单独列出来

该算法在《Model Checking》与《Principles of Model Checking》上均给出了解释与伪码，实现由我自己实现，部分基础性的代码来自《算法》（第四版）的图部分。

Büchi自动机判断接受语言是否为空

根据前文所说，假设p是一个Büchi自动机的可接受运行，那么p中肯定会经过接受状态F无限多次，因此，p中肯定有一部分的序列重复了无限多次，这重复的状态肯定处在一个环里面，也就是说，这些个状态节点组成了强连通图。

基于上述分析，我们将Büchi自动机A接受的语言是否空的问题，转化成如下的形式

如果语言L(A)是非空的，当且仅当有接受状态在一个环里面出现

Tarjan提出的查找强连通图上的深度优先遍历算法（DFS）可以在时间复杂度O(|Q|+|Δ|)内判定一个Büchi自动机是否为空，下面介绍的是一种更加有效的算法，该算法采用双DFS来查找带有接受状态的环，因为嵌套地使用了DSF，该算法被称为Nested Dfs。

算法伪码

算法解释

算法输入：

• Büchi自动机A所代表的的图
• 初始状态集
• 接受状态集

算法输出：

• 是否存在接受状态在图中的环上

我把算法的流程分为如下几个步骤：
1、从初始状态出发，利用深度优先算法搜索某个接受状态是否是可达的
2、如果接受状态是可达的，那么从该接受状态出发，利用第二个深度优先算法搜索该接受状态是否处于在一个环上，同时，标记搜索过的状态
3、如果发现该接受状态处于环上，则终止搜索，算法输出True以及对应的环的路径，如果该接受状态不在环上，则继续第一个搜索，看看下一个接受状态是否可达，并尝试找环
4、直到找到了某个接受状态处于环上，或者搜索完了所有的接受状态，算法结束

代码实现

Digraph.java 带权有向图的数据结构类，采用的是邻接表的方式

import java.util.ArrayList;
import java.util.LinkedHashMap;
import java.util.List;/*** Created on 2020/12/4.* Description：带权有向图类*/
public class Digraph {private int V;  // 有向图的顶点private int E;  // 有向图的边private LinkedHashMap<Integer, List<Integer>> adj;  // 邻接表/*** 使用顶点数初始化有向图** @param V* @throws IllegalArgumentException if(@code V < 0)*/public Digraph(int V) {if (V < 0) throw new IllegalArgumentException("Number of vertices in a Digraph must be nonnegative");this.V = V;this.E = 0;adj = new LinkedHashMap<>();for (int v = 0; v < V; v++)adj.put(v, new ArrayList<>());}/*** 使用另一个图来初始化图** @param digraph*/public Digraph(Digraph digraph) {this.V = digraph.V();this.E = digraph.E();this.adj = digraph.adj();}/*** 返回顶点数** @return*/public int V() {return V;}/*** 返回边的数量** @return*/public int E() {return E;}/*** 返回邻接表** @return*/public LinkedHashMap adj() {return adj;}/*** 添加一条边,id1指向id2** @param id1,id2*/public void addEdge(Integer id1, Integer id2) {// 判断该边是否已经存在for (Integer i: (List<Integer>)adj(id1)) {// 如果已经存在，那么直接返回if (i.equals(id2) )return;}// 如果不存在则加入该边((List<Integer>) adj(id1)).add(id2);}/*** 查找某个顶点的邻接链表** @param id* @return*/public Iterable adj(Integer id) {validateVertex(id);return adj.get(id);}/*** 使用id验证顶点是否存在于图中** @param id*/private void validateVertex(Integer id) {if (adj.get(id) == null) {throw new IllegalArgumentException("vertex " + V + "not in the graph");}}@Overridepublic String toString() {return adj.toString();}
}

Nested Dfs算法类，用于处理算法的计算逻辑

• marked是用于标记第一个Dfs算法遍历过的图节点
• cycleMarked是用于标记第二个Dfs遍历过的图节点，这个标记可以提高算法的效率，因为如果在查找通过第一个接受状态的环时，没有找到环，那么说明再查找之后的接受状态时无需考虑上述已经被遍历过的节点
• 关于查找通过某个接受状态环的算法，其实只需要利用Dfs算法，外加一个辅助栈，栈的作用是记录当前搜索中遍历的路径，如果进入深层的搜索就将状态压入栈，如果结束一次搜索就将状态弹出栈，如果查找到下一个状态就是搜索开始的状态，那么就说明找到了一个环，输出栈中的元素，就是一条环的路径（就如同边走迷宫边放线，走着走着发现从另外路径又回到了起点，那么就找到了一个环）

注意：这个算法只不过是普通查找环算法的小小变种，一般的查找环算法是判断下一个状态是否已经处于栈中，如果是就说明存在环，而这里找的是下一个状态是否是搜索开始的状态。所以该算法仍然只能判断是否存在通过接受状态的环，而且找到哪个环也要看遍历的循序，并不能找到所有的环。

import java.util.HashMap;
import java.util.List;
import java.util.Map;
import java.util.Stack;/*** Created on 2020/12/5.* Description：嵌套dsf算法解决查找某可达节点是否存在通过该节点的环*/
public class NestedDfs {private Map marked;         // marked[v] 是否被标记，用于深度优先搜索private Map cycleMarked;         // cycleMarked[v] 是否被标记，用于查找环private Map edgeTo;            // edgeTo[v] 是否连通private Map onStack;       // onStack[v] 是否有顶点在栈里面private Stack<Integer> cycle;    // 递归调用的栈上的所有顶点public NestedDfs(Digraph graph, Integer[] initStates, Integer[] checkStates) {marked = new HashMap<Number, Boolean>();// 查看它是否能从初始状态开始可达for (Integer initState : initStates) {if (cycle != null) break;for (Integer checkState : checkStates) {dfs(graph, initState, checkState);if (cycle != null) break;}}}/*** 深度优搜索算法，判断两个点之间是否可达** @param G* @param initState* @param checkState*/private void dfs(Digraph G, Integer initState, Integer checkState) {marked.put(initState, true);// 如果有环节退出if (cycle != null)return;// 如果初始状态到检查状态是可达的，那么开始检查是否有通过检查状态的环if (initState.equals(checkState)) {onStack = new HashMap<Integer, Boolean>();edgeTo = new HashMap<Integer, Integer>();cycleMarked = new HashMap<Integer, Boolean>();dfsWithCheck(G, checkState, checkState);}for (Integer i : (List<Integer>) G.adj(initState)) {if (!(boolean) marked.getOrDefault(i, false))dfs(G, i, checkState);}}/*** 到某个顶点是否可达** @param id 顶点id* @return*/public boolean marked(Integer id) {return (boolean) marked.getOrDefault(id, false);}private void dfsWithCheck(Digraph G, Integer id, Integer checkId) {onStack.put(id, true);cycleMarked.put(id, true);for (Integer i : (List<Integer>) G.adj(id)) {if (this.hasCycle()) return;else if (!(Boolean) cycleMarked.getOrDefault(i, false)) {edgeTo.put(i, id);dfsWithCheck(G, i, checkId);} else if ((Boolean) onStack.getOrDefault(i, false) && i.equals(checkId)) {cycle = new Stack<>();for (Integer x = id; !x.equals(i); x = (Integer) edgeTo.get(x)) {cycle.push(x);}cycle.push(i);cycle.push(id);}}onStack.put(id, false);}/*** 是否有循环，有返回true，没有返回false** @return cycle is null?*/public boolean hasCycle() {return cycle != null;}/*** 返回环迭代序列** @return cycle*/public Iterable cycle() {return cycle;}
}

Main.java用于测试算法的准确性
测试用例就选取了红绿灯的例子，给每个TS中的状态表上序号，便于程序的处理，第一个不存在通过接受状态的环，输出为null，第二个存在，输出环的路径

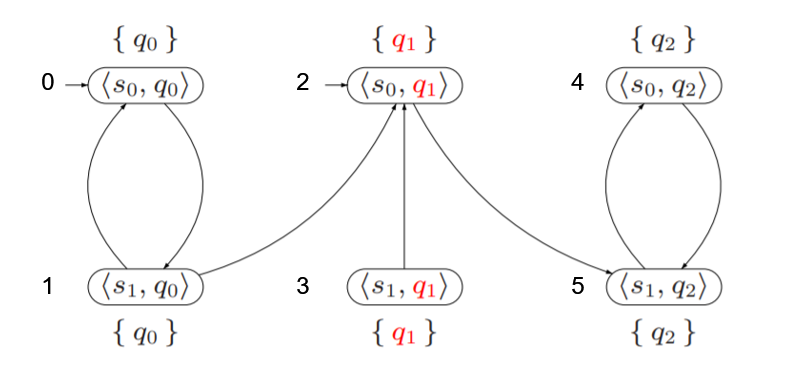
public class Main {public static void main(String[] args) {// 构建图Digraph graph = new Digraph(6);graph.addEdge(0,1);graph.addEdge(1,0);graph.addEdge(1,2);graph.addEdge(2,4);graph.addEdge(3,2);graph.addEdge(4,5);graph.addEdge(5,4);// 输入初始节点和需要判断的点Integer[] initStates = new Integer[]{0,2};Integer[] checkStates = new Integer[]{2};NestedDfs nestedDfs = new NestedDfs(graph, initStates, checkStates);// 输出是否有通过代检查节点的环 以及 输出环的路径System.out.println(nestedDfs.hasCycle());System.out.println(nestedDfs.cycle());// 测试例子2Digraph graph2 = new Digraph(9);graph2.addEdge(0,1);graph2.addEdge(1,0);graph2.addEdge(1,2);graph2.addEdge(2,1);graph2.addEdge(0,4);graph2.addEdge(1,3);graph2.addEdge(3,4);graph2.addEdge(4,3);graph2.addEdge(2,4);graph2.addEdge(5,4);graph2.addEdge(4,8);graph2.addEdge(6,7);graph2.addEdge(7,6);graph2.addEdge(7,8);graph2.addEdge(8,7);Integer[] initStates2 = new Integer[]{1,4};Integer[] checkStates2 = new Integer[]{3,4,5};NestedDfs nestedDfs2 = new NestedDfs(graph2, initStates2, checkStates2);System.out.println(nestedDfs2.hasCycle());System.out.println(nestedDfs2.cycle());}
}