本文主要是介绍【Flink系列二】如何计算Job并行度及slots数量,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
接上文的问题
- 并行的任务,需要占用多少slot ?
- 一个流处理程序,需要包含多少个任务
首先明确一下概念
slot:TM上分配资源的最小单元,它代表的是资源(比如1G内存,而非线程的概念,好多人把slot类比成线程,是不恰当的)
任务(task):线程调度的最小单元,和java中的类似。
---------------------------------------------------------------------------
为更好的去理解后面如何计算并行度及需要的slots数量,先介绍一下几个概念
并行度(Parallelism)

- 一个特定算子的子任务(subtask)的个数被称之为并行度(parallelism)一般情况下,一个stream的并行度,可以认为就是其所有算子中最大的并行度。
- 图中source算子的并行度=2,map算子的并行度=2,keyby算子的并行度=2,sink算子的并行度=1
ps:并行度的设置有3个地方,1=代码中指定,2=提交Job时指定-p参数,3=Flink配置文件conf中执行,其优先级1>2>3, 不详细展开,有问题可以评论区
由图1,我们可以算出stream的任务数=7(两个source + 两个map + 两个keyby + 一个sink)
TaskManager和Slots
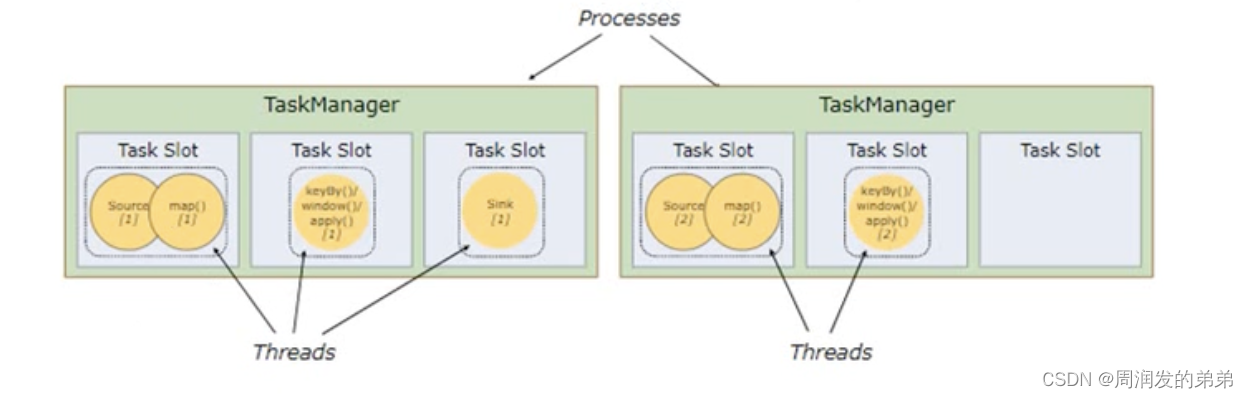
- Flink中每个TaskManager都是一个JVM进程,它可能会在独立的线程上执行一个或多个任务
- 为了控制一个TM(TaskManager缩写)能接受多少哥task,TM通过task slot来进行控制(一个TM至少有1个slot)
- 建议TM中slot数量设置为cpu核心数,因为一个TM中slot内存的独享的,但是cpu是共享的,为避免不同slot执行任务时争抢cpu资源,建议slot数量设置和cpu核心数一致
- 图中slot数量决定了TM上的最大线程并行能力,一个slot可以执行一个线程,也可以串行执行多个线程。
图2中我们看到
- source和map算子合并到一块了,那为什么可以合并呢?
- 合并后每个任务都占用一个slot,一共是占用了5个slot,现实真的是这样的吗?
带着问题,再看一个例子
source和map算子及keyby算子的并行都调整为6,sink算子的并行度还是1,排列方式如图
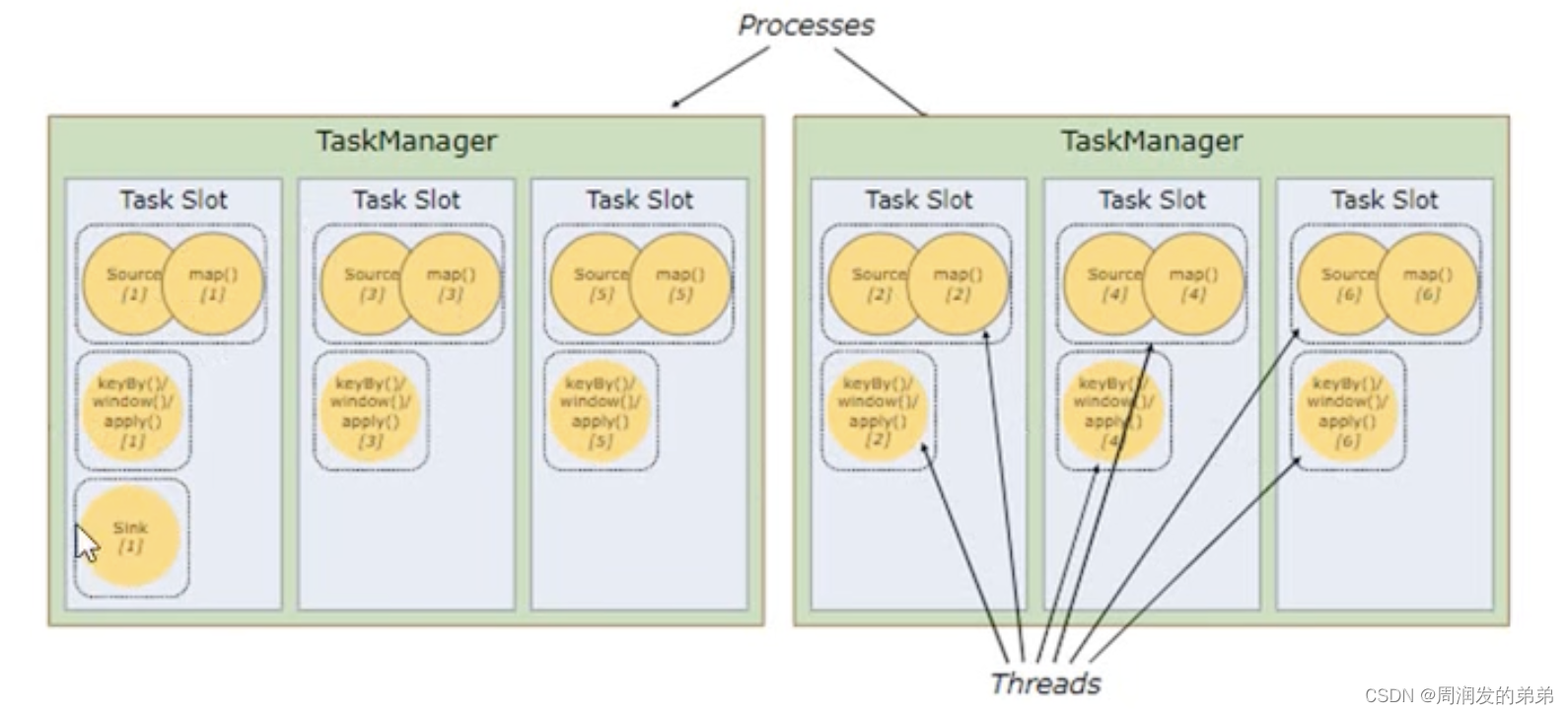
按照我们上面的理解,我们应该需要的slot数量=6+6+1=13,但是这样会造成slot资源的浪费(流处理任务第一个算子处理完了之后需要等后面的算子都执行完,再开始下一批次的任务处理),为此,Flink允许任务共享slot
- 默认情况下,Flink允许子任务共享slot(必须是前后执行的不同的任务),及时他们是不同任务的子任务。这样的结果是,一个slot可以保存作业的整个管道。
- Task slot是静态的概念,是指TM具有的并发的并行执行能力
所以,Flink优化后一共占用6个slot。
slot共享组
- 任务槽共享的好处:
1.Flink 集群所需的 task slot 和作业中使用的最大并行度恰好一样。无需计算程序总共包含多少个 task(具有不同并行度)。
2.资源 容易获得更好的资源利用。如果没有 slot 共享,非密集 subtask(source/map())将阻塞和密集型 subtask(window)
一样多的资源
默认情况下会设置一个默认的共享组, slotSharingGroup("default"),这样所有的算子都可以共享slot;如果想让两个算子任务不共享slot,通过调整共享组来实现。 不同的共享组一定在不同的slot上
// 1. 创建执行环境StreamExecutionEnvironment env = StreamExecutionEnvironment.getExecutionEnvironment(conf);//设置并行度,所有算子都默认这个并行度env.setParallelism(1);DataStreamSource<String> ds = env.socketTextStream("hadoop102", 8888);ds.flatmap(new WordCount.MyFlatMapper()).name("f1").setParallelism(2).slotSharingGroup("a").keyBy(0).sum(1).setParallelism(2).slotSharingGroup("c");.print().setParallelism(1)// 5. 启动执行env.execute();
show plan后我们可以看到slot没有共享,执行stream需要4个slot
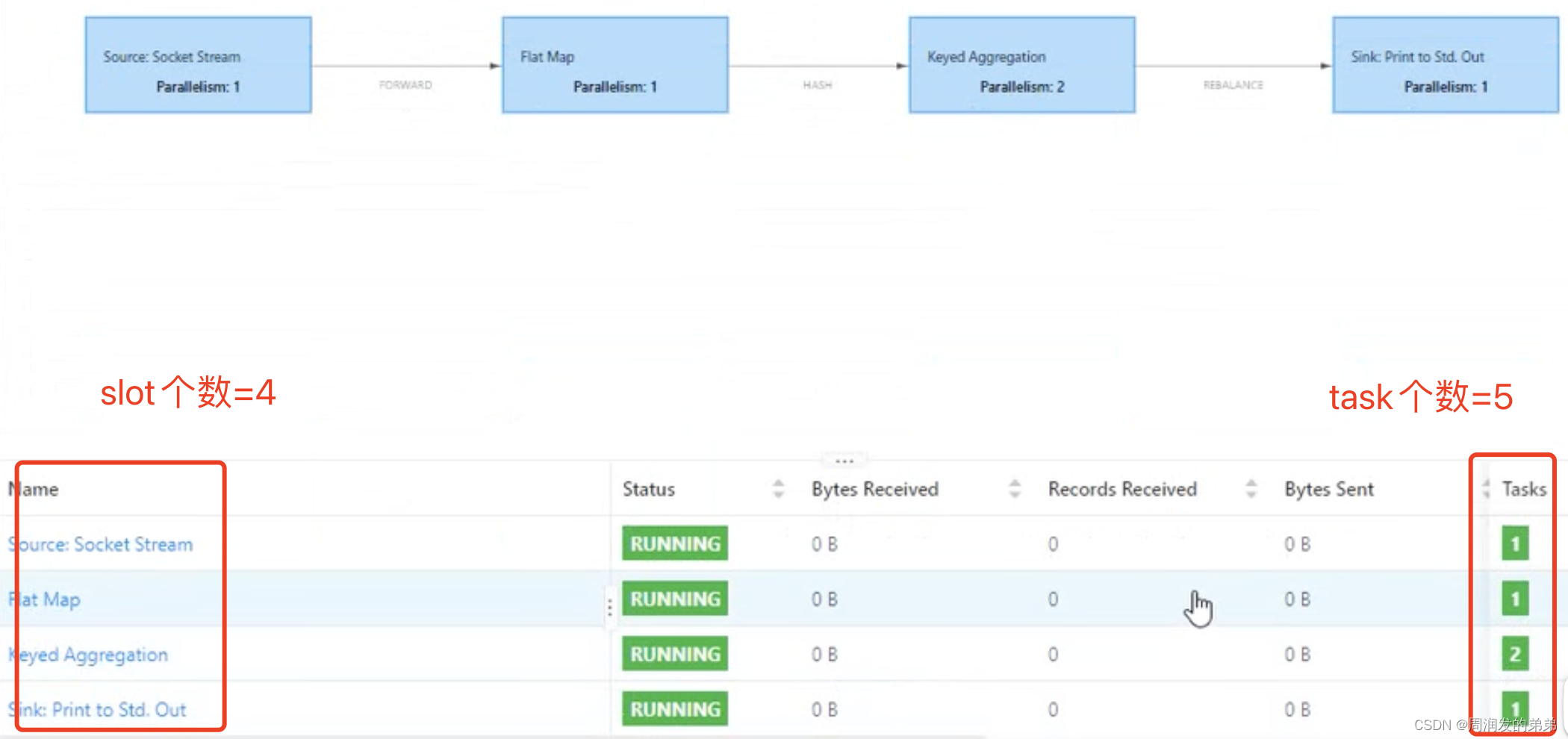
如果不单独设置slot共享组,那么该任务的slot个数=2,
并行子任务的分配
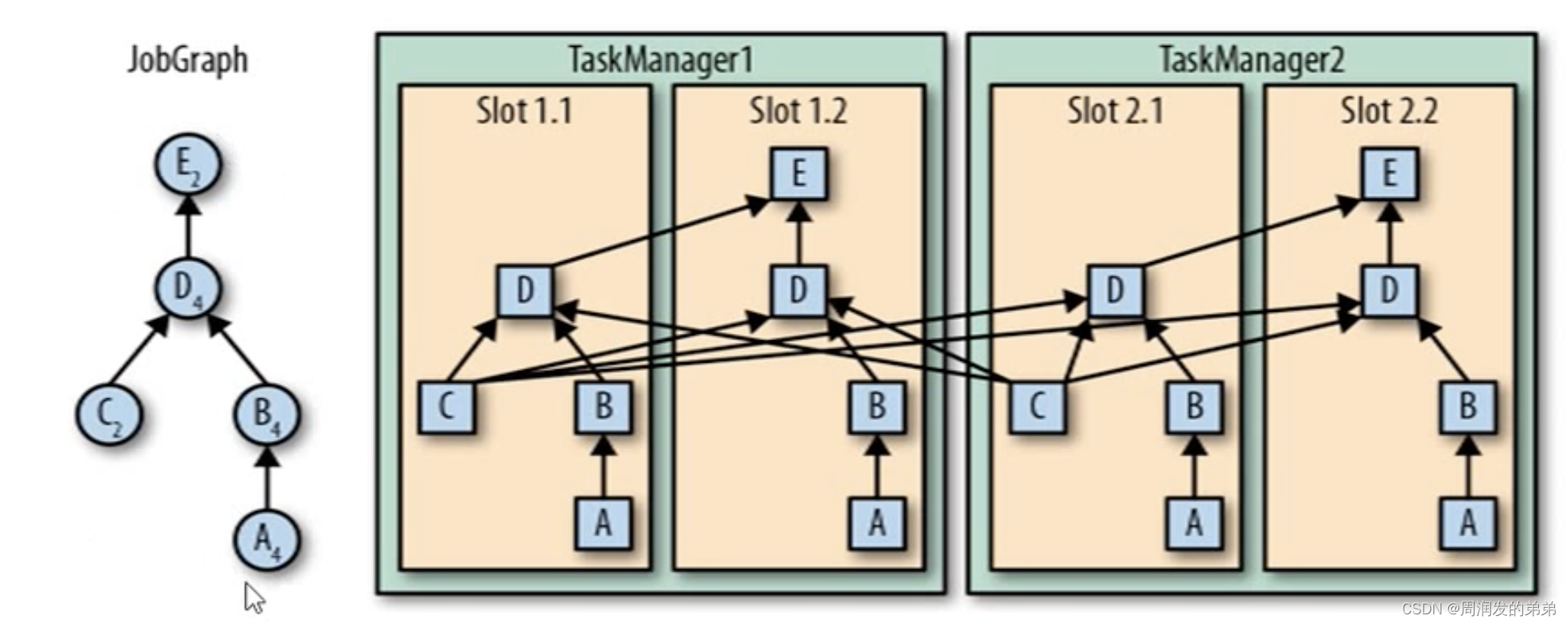
图5中有两条不同的流,每个字母右下角的下标代表并行度,A并行度=4,B并行度=4,C并行度=2,D并行度=4,E并行度=2;
整个任务开启slot共享后,一个会有4+4+4+2+2=16个任务,一共需要申请4个slot;
C->D过程涉及数据的合并,需要将数据copy到D的每个子任务中。
总结
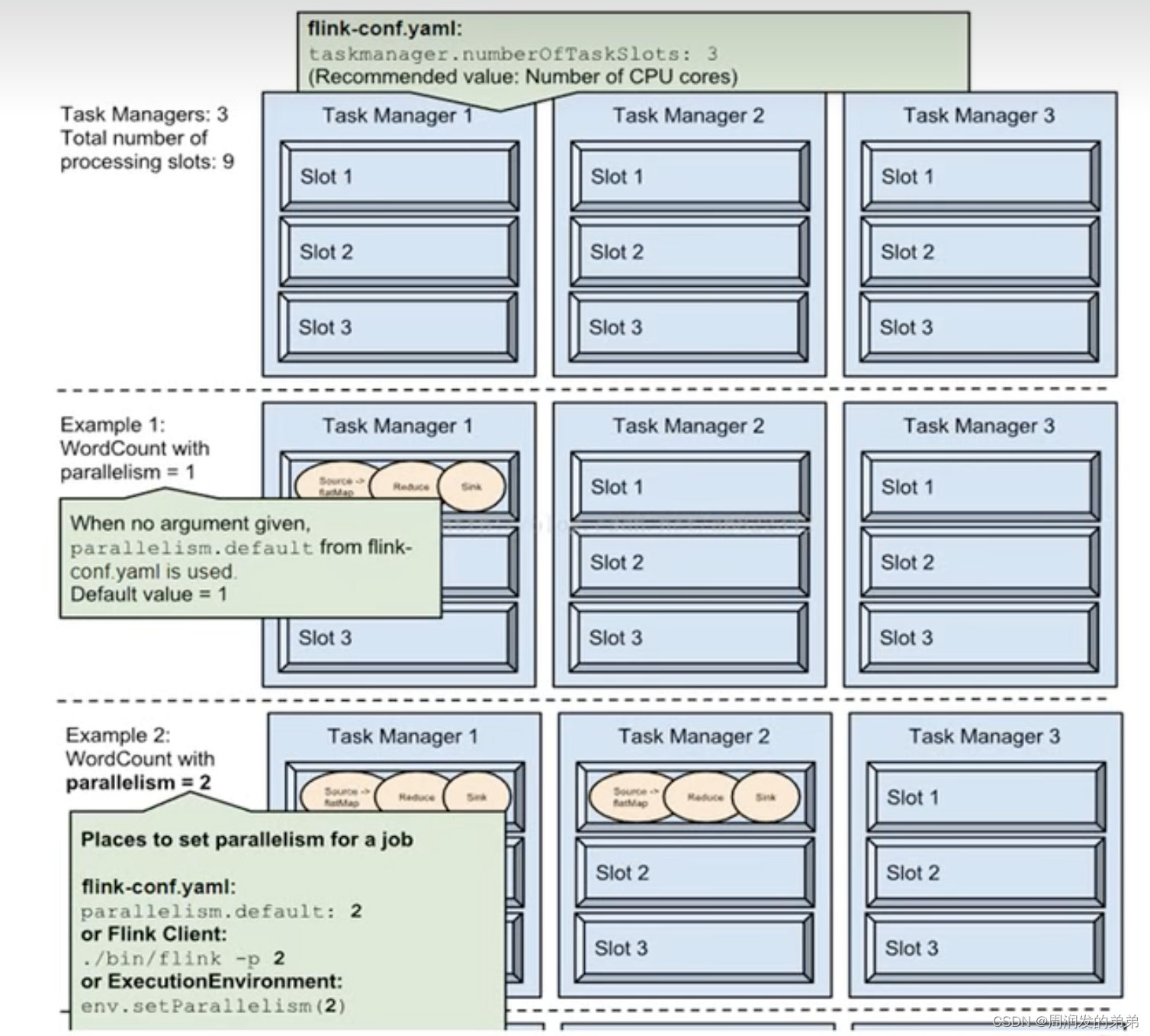
下图中在flink中配置文件flink-conf设置的并行度是3,flink集群中TM数量=3,每个TM中slot数量=3
Example1中代码中设置的paeallelism=1,并且允许slot共享,所以会占用1个slot,3个算子任务
Example1中代码中设置的paeallelism=2,并且允许slot共享,所以会占用2个slot,6个算子任务
这篇关于【Flink系列二】如何计算Job并行度及slots数量的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




