台湾国立大学郭彦甫Matlab教程笔记（16）数值微分 numerical differentiation

本文主要是介绍台湾国立大学郭彦甫Matlab教程笔记（16）数值微分 numerical differentiation，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

台湾国立大学郭彦甫Matlab教程笔记（16）数值微分 numeric differentiation

复习：diff()函数用来计算vector前后 entry的差异

数值微分继续

various step size 不同Δx大小

不同Δx大小，看近似值和真正函数值之间的差异大不大。

看题目，用不同的h值计算函数f(x)=sin(x)的导数，画出图形

The derivatives(导数) of f(x)=sin(x) calculated using various h values

codes：

g=colormap(lines);hold on;
for i=1:4%为了给出不同的h值x=0:power(10,-i):pi;%power(10,-i)表示10的-i次方
y=sin(x);
m=diff(y)./diff(x);%算是计算导数
plot(x(1:end-1),m,'color',g(i,:));%x(1:end-1)因为diff差值，vector维度少一
end
hold off;set(gca,'xlim',[0,pi/2]);%设置x轴横坐标范围
set(gca,'ylim',[0,1.2]);
set(gca,'xtick',0:pi/4:pi/2);%设置x轴坐标间隔
xticklabels({'0','\pi/4','\pi/2'});%显示pi
set(gca,'fontsize',18);%设置字体
h=legend('h=0.1','h=0.01','h=0.001','h=0.0001');%设置图像名称
set(h,'fontname','Times New Roman');
box on;%右上边框显示

代码的解释
colormap回顾：colormap输入参数的用法
在这里插入图片描述

plot(x(1:end-1),m,‘color’,g(i,:));的解释：
%x(1:end-1)因为diff差值，vector维度少一，所以需要end-1。这里color用的是g(i,:),由于g是colormap中的lines颜色图，颜色图是一个矩阵matrix，这里应该是二维的，g(i,:)取的是这个矩阵的第i行元素，我的理解是一个行向量，然后赋值给了color显示出来。

运行结果:

在这里插入图片描述
作业题：
给定一个函数，用不同的h值计算近似导数

在这里插入图片描述
我的代码：

g=colormap(lines);%颜色
hold on;
%先来确定x的范围：
for i=1:3x=0:power(10,-i):2*pi;%不同的h 步长y=exp(-x).*sin(x.^2/2);%函数表达式需要点乘m=diff(y)./diff(x);%差分，求导plot(x(1:end-1),m,'color',g(i,:));
end
hold off;%下面是一些设置
box on;
set(gca,'fontsize',18);
set(gca,'xlim',[0,2*pi]);%x轴范围
set(gca,'ylim',[-0.3,0.3]);%y轴范围
set(gca,'xtick',0:pi/2:2*pi);%刻度
xticklabels({'0','\pi/2','\pi','3\pi/2','2\pi'});%显示刻度
legend('h=0.1','h=0.01','h=0.001');%函数标头

有个问题:这个函数表达式是两个函数相乘的形式，中间是用*还是用.*点乘？
实验结果：
y=exp(-x).*sin(x^2/2);（错误）
在这里插入图片描述
计算这个表达式正确的形式

y=exp(-x).*sin(x.^2/2);

我的练习结果：

在这里插入图片描述
下一个题目是

二次和三次微分second and third derivatives

the second derivative f’’ and third derivative f’’’ can be obtained using similar approaches

举例子：
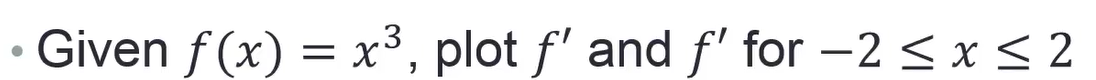
在这里插入图片描述

例程代码：

x=-2:0.005:2;
y=x.^3;
m=diff(y)./diff(x);%一次微分
m2=diff(m)./diff(x(1:end-1));%二次微分plot(x,y,x(1:end-1),m,x(1:end-2),m2);%作图
xlabel('x','fontsize',18);
ylabel('y','fontsize',18);
legend('f(x)=x^3','f''(x)','f'''(x)',4);%函数标头 
set(gca,'fontsize',18);

【注意】每做一次微分，entry就少一个。

运行结果：
在这里插入图片描述