USACO2023Feb Silver

T1 T2 AC, T3 RE, 722/1000 pts, promoted to Gold.

T1 Bakery

二分答案 - WA(0pts)

把$t_C,t_M$记作$C,M$以便书写。

$(x,y)$满足若干个形如$a_i(C-x)+b_i(M-y)\le c_i$的不等式，求$(x+y{)}_{min}$.
具备单调性，考虑二分答案。
设$x+y=s$, 则不等式化为$(a_i-b_i)x\ge a_{i}C+b_{i}M-b_{i}s-c_i$, 讨论$a_i-b_i$的正负，解出$x$的范围，大于等于或小于等于某个值。这里涉及到除法，我选择实数存储。
有多个这样的不等式，可得x的区间$[mn,mx]$，若区间不为空，即$mn\le mx$，则x有解，s合法——我当时是这样认为的。

时间复杂度$O(TNlogt)$.

无法把变量命名为tm，本机上编译错误，卡了我很久。

交上去WA，我先做了后面两题再回来，以为是浮点数的精度不够，改成分数交叉相乘比较大小，还是WA。

又读了一遍题目，发现C和M不能被减成非正数（做到一半忘了这一点），也就是说x有一个初始区间$[C-1,s-M+1]$, 以及$[0,s]$. 把这个加了上去，还是WA，我无计可施。

int tt, n;
ll a[MAXN], b[MAXN], c[MAXN], tc, m;bool check(ll s) {db mx = min(s, tc - 1), mn = max(0LL, s - m + 1);for (int i = 1; i <= n; ++i) {db val = (db)1.0 * (a[i] * tc - b[i] * s - c[i] + b[i] * m) / (a[i] - b[i]);if (a[i] > b[i]) ckmax(mn, val);else if (a[i] < b[i]) ckmin(mx, val);else if (a[i] * tc - b[i] * s > c[i] - b[i] * m) return false;}return mn <= mx + 1e-8;
}int main() {scanf("%d", &tt);while (tt--) {scanf("%d%lld%lld", &n, &tc, &m);for (int i = 1; i <= n; ++i) {scanf("%lld%lld%lld", a + i, b + i, c + i);}ll l = 0, r = tc + m - 2;while (l < r) {ll mid = (l + r) >> 1;if (check(mid)) r = mid;else l = mid + 1;}printf("%lld\n", l);}return 0;
}

ll gcd(ll x, ll y) {return x % y == 0 ? y : gcd(y, x % y);
}struct Node {ll a, b;Node(ll _a, ll _b) {if (_b < 0) a = -_a, b = -_b;else a = _a, b = _b;if (a * b) {ll g = gcd(abs(a), abs(b)); a /= g; b /= g;}}bool operator < (const Node &x) const {return a * x.b < b * x.a;}
};bool check(ll s) {Node mx = Node(min(s, tc - 1), 1), mn = Node(max(0LL, s - m + 1), 1);for (int i = 1; i <= n; ++i) {Node val = Node(a[i] * tc - b[i] * s - c[i] + b[i] * m, a[i] - b[i]);if (a[i] > b[i]) ckmax(mn, val);else if (a[i] < b[i]) ckmin(mx, val);else if (val.a > 0) return false;}return !(mx < mn);
}

二分答案 - AC

She can’t upgrade her oven a fractional amount of times,

我曾反复读题，每次读到这句话，我都认为这是一句废话，没考虑到自己就是因这一点而错了。
x是整数，所以解集并不是非空即可，而是有整数解。

bool check(ll s) {// ...... ......return ceil(mn) <= floor(mx);
}

T2 Cow-libi

二分查找 - AC

把所有案件按时间排序。

已知牛在时间点 $t$ 的位置，它要完成所有犯罪的必要条件是：它可能完成发生在 $t$ 之前最晚，以及 $t$ 之后最早的犯罪。
例如，有4起案件分别发生在100、200、300、400这三个时候。150时间点的牛如果无法证明自己无辜，那他可能完成100、200的犯罪；如果牛在300时间点，那就只考虑300这一起案件。

这个必要条件具备充分性吗？换言之，能完成前后最近的犯罪，就能完成所有犯罪吗？注意到题面中"It will always be possible for a single cow to travel between all grazings"，所以这个条件充要。

所以，只需要检测最多两起案件，就能完成检测：办不到其中任意一个，牛就是无辜的。时间复杂度$O(NlogG)$.

struct Node {ll x, y, t;bool operator < (const Node &X) const {return t < X.t;}
} a[MAXG];int g, n, ans;int search(ll tar) {if (tar > a[g].t) return g + 1;int l = 1, r = g;while (l < r) {int mid = (l + r) >> 1;if (a[mid].t >= tar) r = mid;else l = mid + 1;}return l;
}bool check(ll x, ll y, ll t, int p) {return (x - a[p].x) * (x - a[p].x) + (y - a[p].y) * (y - a[p].y) > (t - a[p].t) * (t- a[p].t);
}int main() {scanf("%d%d", &g, &n);for (int i = 1; i <= g; ++i) {scanf("%lld%lld%lld", &a[i].x, &a[i].y, &a[i].t);}sort(a + 1, a + g + 1);for (int i = 1; i <= n; ++i) {ll x, y, t; scanf("%lld%lld%lld", &x, &y, &t);int pos = search(t);bool flag = false;if (pos > 1) flag |= check(x, y, t, pos - 1);if (pos <= g) flag |= check(x, y, t, pos);ans += flag;}printf("%d\n", ans);return 0;
}

T3 Moo Route II

虚边、搜索 - RE

把所有到达时间加上到达机场的滞留时间，避免滞留时间带来的麻烦。

(k,m)表示一个状态（图中的一个节点），在k机场，时间是m。根据航班建边。
但是这还不够，因为Bessie可以在某个机场停留一段时间后，再进行下一次飞行。也就是说，时间流逝会带来在同一机场不同时间带来的状态改变。
我的第一反应是建虚边和虚点以实现状态的改变。如图，11连到12，12连到13……这显然会爆空间。
实际上，航班信息中如果只提到了(2,11)和(2,17)，那只需在这两个点之间建虚边即可，无需建虚点。所以在某个机场提到的所有时间点排序后，依次连边即可。

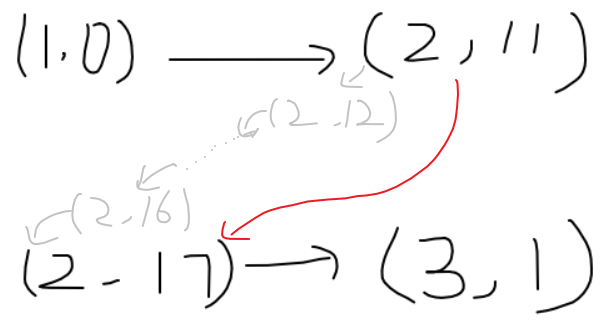
建完图后，从(1,0)开始搜索，连通到的点中打擂台。

最多$2\times M+1$个点，时间复杂度$O(MlogM)$. 不知为何RE.

struct Node {int k, t;
} nodes[MAXM << 1];int n, m, c[MAXN], r[MAXN], d[MAXN], s[MAXN], a[MAXN], cnt, ans[MAXN];
bool vis[MAXM << 1];
vector<int> g[MAXN], h[MAXM << 1];
map<pair<int, int>, int> ind;int get(int k, int t) {pair<int, int> p = make_pair(k, t);if (ind.find(p) == ind.end()) {nodes[++cnt].k = k; nodes[cnt].t = t;g[k].push_back(t);ind.insert(make_pair(p, cnt));return cnt;}return ind[p];
}void add(int u, int v) {h[u].push_back(v);
}void dfs(int u) {vis[u] = true;ckmin(ans[nodes[u].k], nodes[u].t);for (int i = 0; i < h[u].size(); ++i) {int v = h[u][i];if (!vis[v]) {dfs(v);}}
}int main() {memset(ans, 0x3f, sizeof(ans));scanf("%d%d", &n, &m);for (int i = 1; i <= m; ++i) {scanf("%d%d%d%d", c + i, r + i, d + i, s + i);}for (int i = 1; i <= n; ++i) {scanf("%d", a + i);}g[1].push_back(0); get(1, 0);for (int i = 1; i <= m; ++i) s[i] += a[d[i]];for (int i = 1; i <= m; ++i) {int u = get(c[i], r[i]), v = get(d[i], s[i]);add(u, v);}for (int i = 1; i <= n; ++i) {sort(g[i].begin(), g[i].end());for (int j = 0; j < g[i].size() - 1; ++j) {int u = get(i, g[i][j]), v = get(i, g[i][j + 1]);add(u, v);}}dfs(1);a[1] = 0;for (int i = 1; i <= n; ++i) {if (ans[i] < INF) printf("%d\n", ans[i] - a[i]);else printf("-1\n");}return 0;
}

RE的原因 - AC

g[i].size() - 1
不能直接减，应将STL容器的size强转为int.

另一种搜索（补）

上面的方法将每个机场根据时间维度拆成多个点。

也可以不拆。对于每条边，记录起飞和到达时间，对每个点以起飞时间为关键字排序出边。这样，某时间在一个机场，枚举所有能走的出边。
显然每条边只会被走一次，所以对每个机场记录一个指针，标记从某个时间往后的出边都被走过了，保证时间复杂度。