串匹配之bm算法

本文主要是介绍串匹配之bm算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

以终为始

在串匹配之kmp算法中，已经简单介绍了kmp算法的基本原理与实现。kmp算法的基本思想，是利用已经成功匹配的字符的信息，快速跳过无意义的对齐位置，从而实现更高的效率。下面，我们首先对这样的思想进行更深入的研究。

在实际的串匹配问题中，字符集的规模往往是挺大的，比如说英文字符集，就至少有52个字符，更不要提ASCII码，还有中文字符集了。这样，在随机的情况下，一次比对成功的概率只有1/52，并且多次比对成功的概率以指数的速率减小，比对的次数服从几何分布，期望的比对次数仅有一次。在这种情况下，即使是蛮力算法，其时间复杂度也只有O(n + m)。

在一般的串匹配问题中，模式串的规模较小而文本串的规模往往极大，比如在一篇论文中查找某个英文单词的情形，在这种情况下，文本串中往往具有大量模式串中不会出现的字符。设想如果在任意一个对齐位置，模式串与文本串是从后往前比对，此时一旦在文本串中出现模式串中不存在的字符，就可以将整个模式串移出这个字符，从而跳过大量无意义的对齐位置。如下图所示：

compare_backwards

如我们前面指出的那样，这种情况在头几次比对中出现的概率是极高的，因此相对于自左向右的比对，将比对的方向变成自右向左，的确可以极大地提高串匹配的效率。

bm-bc策略

坏字符(bad character, bc)策略是一种非常简明的策略。它的基本思想是，在自后向前的某次匹配中，一旦在某个位置k比对失败，则将模式串整体右移，并且重新从右至左开始新一轮的比对，将比对失败的字符称为坏字符。而要使下一个对齐位置能够匹配，则至少要在坏字符处能够匹配才行，如下图所示：

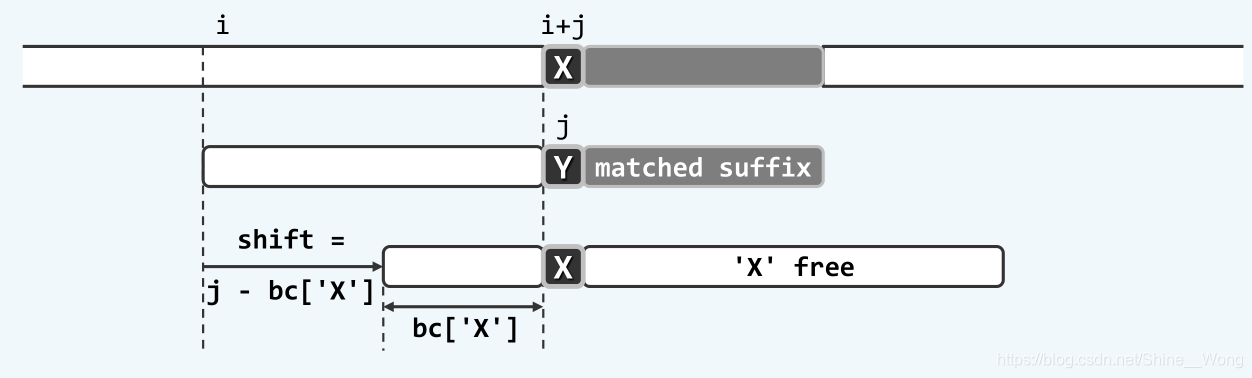
bad_character

因此，坏字符策略实现的关键，就在于找到模式串中，位于坏字符Y左侧，并且与字符X能够匹配的下一个字符。应该指出的是，这样的字符能够有多个，也就对应了多个移动距离，所有这些移动距离都是值得对齐的。因此，为了不错过其中的任意一个字符，应该取移动距离最小的那一个，使之与文本串中的X对齐。

为了快速地确定下一个对齐位置，可以仿照kmp算法的思路，对于模式串中出现过的所有字符，保存每个字符出现的最后位置，构成bc表，以便在字符匹配时迅速更新对齐位置。因此，bc表就有 $\left|\Sigma\right| + 1$ 项，其中 $\Sigma$ 为模式串的字符集，并且将额外的一项用来代表所有没有在模式串中出现过的字符，此时直接将模式串整体移过该字符。

这样，bm-bc策略就可以利用bc数组来快捷地实现了。在一次匹配失败后，比如失败位置j处文本串字符为X，查询bc表会有三种情况：

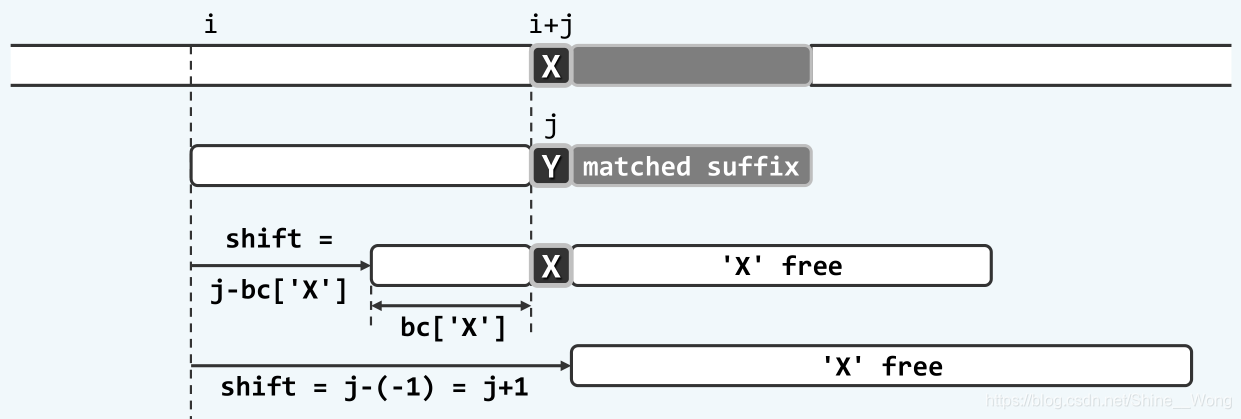
一是bc[X]的确存在，并且bc[X] < j，此时直接将bc[X]处的字符平移到与文本串中的X对齐，即可开始新一轮的比对，此时模式串移动的距离应该是j - bc[X]；另一种情况是X没有出现在模式串的字符集中，此时应该将模式串整体移动字符过X，即移动的距离的j + 1，为了与上面的情况统一，可以令bc[*] = -1，其中*表示所有没有出现在模式串中的字符，另一种理解方法是认为在模式串的左侧P[-1]存在一个通配符可以与X匹配。这两种情况如下图所示：

bc_case12

最后一种情况是bc[X]存在，但是bc[X] > j，即P[bc[X]]出现在P[j]的右侧，此时显然是不可以将P[bc[X]]与文本串中的X对齐的，因为此时将造成模式串的左移。实际上，这种对齐早在之前的比对中就已经被排除掉了。这种情况下，不妨简单地让模式串右移一个单位，然后从右至左开始新一轮的比对。该情况如下图所示：

bc_case3

这样，可以形成下面基于bm-bc策略的串匹配代码：

int match(char* text, char* pattern){int *bc;makeBC(text, &bc);int m = strlen(pattern), n = strlen(text);int i, j;for(i = 0, j = m - 1;i + j < n;){while((j >= 0) && (pattern[j] == pattern[i + j])) --j;if(j < 0) break;//elsei += (bc[text[i + j]] < j? j - bc[text[i + j]]: 1);j = m - 1;}delete [] bc;return i;
}

`bc`表的构建

实际上，在前面的讨论中，已经涉及到了如何构造bc表的问题，这里做一个统一的总结。为了构造bc表，需要遍历模式串中的每一个字符，并且把每个字符X最后出现的位置保存在bc[X]中。为了简单起见，这里的bc表包含全部字符集，比如整个ASCII码字符集，这样便于判断某个字符是否出现在模式串当中，否则还需要额外建立一个散列表或者位图，还是需要消耗同样的空间，因此这里的bc表兼具了给出移动位置以及散列表的作用。

在bc表的构建中采用画家算法(painter’s algorithm)，即从左至右遍历模式串，对于其中每一个出现的字符，都将其位置（或者秩）更新到其在bc表中对应的项中，这样，遍历结束时bc表保存的就是所有字符最后出现过的位置了，因为bc表中各项的值，只取决于该字符最后一次出现的位置，类似于画家作画时，画布上的某处最终的颜色，仅取决于画家在该处的最后一笔，因此称之为画家算法。bc构造的算法如下：

void makeBC(char* const pattern, int* bc){bc = new int[256];for(int ix = 0; ix != 256; ++ix)bc[ix] = -1;                             //initialize to -1for(int ix = 0; pattern[ix] != '\0'; ++ix)bc[pattern[ix]] = ix;                    //painter's algorithm
}

使用bc策略时，最好可以达到O(n/m)的时间复杂度，对应了每次都在最右一个字符匹配失败，然后整体右移m个单位的情况，如下图所示：

bc_bestcase

这固然是一个非常好的结论，但是bc策略在最坏情况下却会达到O(mn)的时间复杂度，与蛮力策略相当，该情况如下图所示：

bc_worstcase

可以看到，在这种情况下，每次都需要进行m - 1次比对，才能在最左侧一次比对中失败，而该次失败只能让模式串右移一个单位。这种情况正与蛮力策略的最好情况相一致。一般地，单次匹配成功的概率越大，即字符集越小，就越接近于这种最坏的情况；单次匹配成功的概率越小，即字符集越大，就越接近于最好的情况。

bm-gs策略

对上述bc策略低效的原因进行分析，可以发现这是因为bc策略中只利用到了匹配失败的坏字符，而在坏字符之前的那多次成功比对却直接被bc策略忽略了。在上面的这种情形中，如果注意到最左侧的1与其右侧四个字符均不相等，一次比对失败后可以直接跳过这四个无意义的对齐位置，从而规避了这种低效的情况。

基于上面的考虑，我们这里提出好后缀(good suffix, gs)策略。顾名思义，好后缀策略就是要将某次比对失败前的成功比对信息加以利用，因此它的思想和kmp算法是一致的。具体说来，就是要利用这些成功比对的信息，将模式串直接移动到下一个值得对齐的位置，那么这里的值得对齐的位置和kmp算法是否存在异同呢？

设某次比对失败于模式串的位置j，因此P[j+1, m)与文本串中的对应字符依次相等。一般地，如果这m - j -1个字符在模式串中左侧的另一位置再次出现，则显然是一个值得的对齐位置，如下图所示：

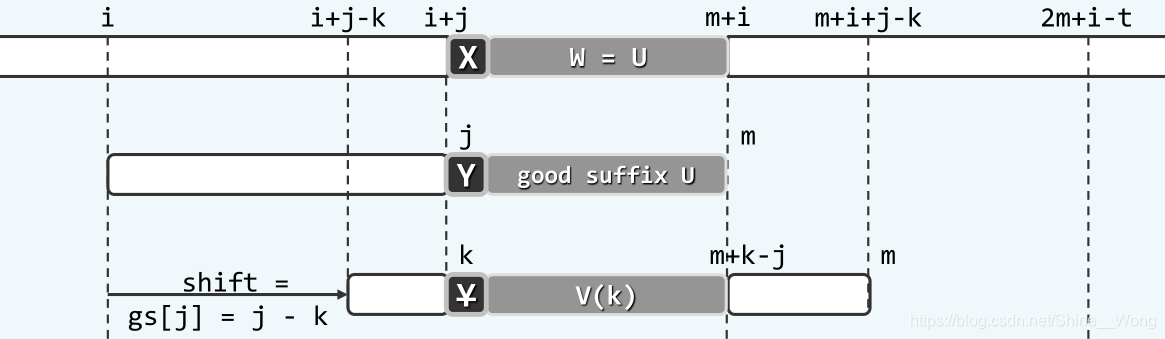
gs_case1

但是如果这m - j - 1字符没有在模式串中重复出现，是否就不存在值得的对齐位置了呢？答案是否定的，因为此时的情形就类似kmp的情形了啊，一般地，如果模式串存在一个前缀，与子串P[j+1, m)的后缀相互匹配，那么这也是一个值得的对齐位置，如下图所示：

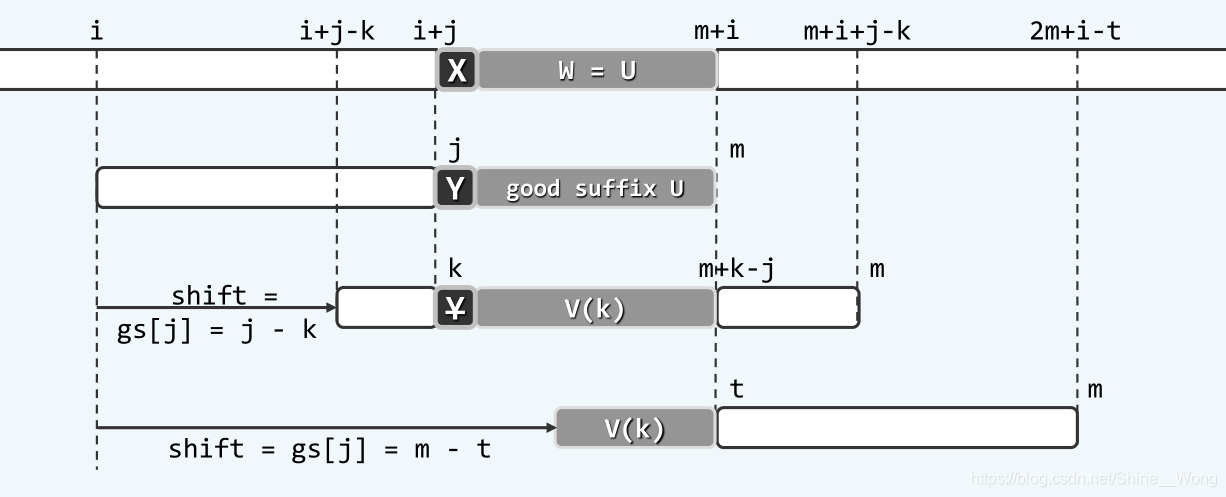
gs_case2

和bc算法和kmp算法一样，如果这样的对齐位置有多个，应该取出其中移动距离最短的一个，从而不会错过其他的对齐位置。并且仿照bc策略和kmp算法的思想，可以预先构造一个gs表，其中gs[i]表示在第i个位置比对失败后，按照好后缀策略应该采取的位移量。这样，就可以通过bc表和gs表把两个策略结合起来，具体说来，由于两个策略都是给出可能匹配的必要条件，因此值得对齐的位置一定同时满足这两个必要条件，在一次匹配失败后，可以同时查询gs[i]和bc[i]，并且选择它们给出的移动距离的最大值，来作为最终的移动距离，具体的代码如下：

int match(char* text, char* pattern){int *bc, *gs;makeBC(text, &bc);gs = buildGS(pattern);int m = strlen(pattern), n = strlen(text);int i, j;for(i = 0, j = m - 1;i + j < n;){while((j >= 0) && (pattern[j] == pattern[i + j])) --j;if(j < 0) break;//elsei += MAX(gs[j], j - bc[text[i + j]]);j = m - 1;}delete [] bc;delete [] gs;return i;
}

需要指出的是，gs表是只依赖于模式串P本身的，这是因为和kmp类似，文本串的相关字符已经全部和模式串匹配了。以下就主要讨论如何高效地构造gs表，而这个问题非常复杂，我只能尽量…

gs表的构造

还是首先考虑蛮力策略吧，为了找到gs表中的任意一项，如gs[i]，根据gs表的语义，应该从位置i往前遍历整个模式串，直到出现上面讨论过的两种情况位置，其最坏情况下的时间复杂度为O(m^2)，因此蛮力算法构造gs表的时间复杂度为O(m^3)。而这里要介绍的一种O(m)构造gs表的策略，你就知道它有多难了。

ss表

为了构造gs表，首先引入ss表的概念——ss[i]是表示在P[0, i]的所有后缀中，与P的某一后缀匹配的最长长度，即最长匹配后缀(maximum matched suffix)的长度。如下图所示：

ss_definition

如果可以成功地构造出ss表的话，就可以用ss表快捷地构造出gs表，因为ss表中包含了gs表中的全部信息。

ss -> gs

这里先讨论如何通过ss表构造出gs表。

实际上，对应于上面提到的好后缀的两种情形，由ss表构造gs表也无非两种情况。第一种情况是ss[j]对应的最长匹配后缀延伸到了P的最左侧，此时有

ss[j] == j + 1;

如下图所示：

ss2gs_case1

此时，对于模式串中所有的秩为i的字符，如果有i < m - j - 1，则MS[j]都是在该处匹配失败的一个候选对齐位置，对应了上面好后缀的第二种情形，此时它们的移动距离距离都是m - j - 1，即m - j -1必然是gs[i]的一个候选。需要指出的是，这种情形并不适用于i >= m - j - 1的情形，因为首位两个子串完全匹配，在该位置对齐后的下一次匹配必然会失败。

第二种情形是ss[j]是P[0, j]的一个真后缀，此时有

ss[j] < j + 1;

如下图所示：

ss2gs_case2

在这种情况下，MS[j]只能作为在位置m - ss[j] - 1处比对失败的候选对齐位置。这是因为，假如i > m - ss[j] - 1，这里的情形与上面讨论的一致，两个子串完全匹配，在该位置对齐后的下一次匹配必然会失败；而假如i < m - ss[j] - 1，由于ss[j]的最值性，MS[j]的前一个字符必然与P[m - ss[j] - 2]不相等，因此这并不是一个有意义的对齐位置。综上，此时m - j - 1是gs[m - ss[j] - 1]的一个候选。

将上述两种情况进行综合，可以得到下面的通过ss表构造gs表的算法：

int* buildGS(char* P){int* ss = buildSS(P);int m = strlen(P);int* gs = new int[m];//initializefor(int j = 0; j < m; ++j) gs[j] = m;for(int i = 0, j = m - 1; j >= 0; --j)if(ss[j] == j + 1)while(i < m - j - 1)              //double loop?gs[i++] = m - j - 1;for(int j = 0; j < m - 1; ++j)            //painter's algorithmgs[m - ss[j] - 1] = m - j - 1;delete []ss;return gs;
}

需要对上面的算法做一些说明。可以看到，在构造gs表时，是使用画家算法，优先对ss的第一种情形进行判断，再使用第二种情形的结果来覆盖第一种情形。实际上，ss的第二种情形的确是优先于第一种情形的，可以证明，对于同一位置i，ss的第二种情形对应的位移量一定小于第一种情形，可以画个图自己看看（留作习题答案略，读者自证不难

然后对两种情形的两次循环，其方向是不一致的。第二个for循环（第一种情形的循环），对于每个位置i，是直接写入它的最短移动距离，因此是从右到左的循环。而第三个for循环（第二种情形的循环）由于是使用画家算法，需要不断覆盖之前的结果，所以是从左到右的循环，这样后写入的结果才是移动距离更短的。容易看出，由ss表构造gs表的算法，其时间复杂度只有O(m)，可以注意到其中是有一个二重循环的，但是由于gs表中的每个位置至多写入一次，因此该循环还是至多只会被执行O(m)次。

那么接下里的问题，就是如何构造ss表了！

ss表的构造

首先还是先考虑一下如何通过蛮力来构造ss表，对于ss表中的每一项ss[i]，需要从该位置向前遍历，来找到一个最长匹配后缀，最坏情况下的时间复杂度为O(m)，因此蛮力算法的总体时间复杂度为O(m^2)。

下面介绍一种在O(m)时间内构造ss表的策略，这个策略连我邓公没有讲清楚，我就瞎写点东西…

这种策略的基本思路是，对于ss[j]，应该利用此前的构造ss的匹配信息，从而快速的更新当前的ss[j]。简单说来有两种情形：

第一种情形如下图所示：

buildss_case1

在构造ss表的过程中，动态地保存和更新之前的极大匹配后缀，分别用lo和hi来表示它的范围，即P(lo, hi]。此时j位于lo和hi之间，因此就可以找到这样一个位置m - hi + j - 1，以这两个位置为后缀的子串，至少拥有j - lo个完全匹配的字符。第一种情形是

ss[m - hi + j - 1] <= j - lo

此时，得益于ss的最值性，P的长度为ss[m - hi + j - 1]的后缀，必然是与P[0, j]匹配的最长匹配后缀，因此ss[m - hi + j - 1必然是ss[j]的最大取值，因此可以直接更新

ss[j] = s[m - hi + j - 1];

倘若不满足第一种情形的条件，即

ss[m - hi + j - 1] > j - lo

则对应了这里的第二种情形，如下图所示：

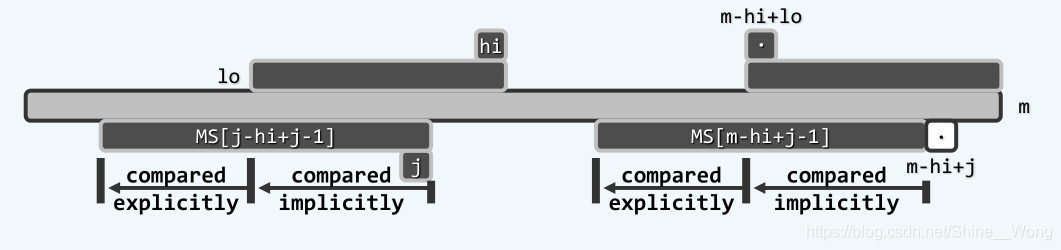
buildss_case2

在这种情况下，根据已有的信息，只能知道P(lo, j]与P(m - hi + lo - 1, m - hi + j - 1]是相互匹配的，因此P(lo, j]与P(m + lo - j - 1, m - 1]是相互匹配的，故ss[j]至少为j - lo。此时，MS[j]有可能继续向左侧扩展，因此需要依次对接下来的字符进行比对。此时将更新hi = j，并在一次比对成功后更新lo的值，即--lo，直到这样的比对失败，即可确定当前的ss[j]。

从这里也可以看出，lo和hi的更新是为了保证对接下来要进行确定字符，进行一个尽可能大的覆盖，而并非只是单纯地维护匹配后缀的最大值，以保证后面要遍历到的位置，尽可能地处于lo和hi的包围中，从而可以应用这里的两种情形。

因此，可以形成下面构造ss表的代码：

int* buildSS(char* P){int m = strlen(P);int* ss = new int[m];ss[m - 1] = m;for(int lo = m -1, hi = m - 1, j = lo - 1; j >= 0; --j){if((lo < j) && (ss[m - hi + j - 1] <= j - lo)){//case oness[j] = ss[m - hi + j - 1];}else{hi = j; lo = __min(lo, hi);while(( 0 <= lo) && (P[lo] == P[m - hi + lo - 1]))--lo;ss[j] = hi - lo;}}return ss;
}