空间相关分析(三) 局部莫兰指数的理解与计算

本文主要是介绍空间相关分析(三) 局部莫兰指数的理解与计算，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

        在上篇中，我们详细地阐述了全局莫兰指数(Global Moran’I)的含义以及具体的软件实操方法。今天，就来进一步地说明局部莫兰指数(Local Moran’I)的含义与计算。

        首先说明一下进行局部相关分析的必要性：

1. 在全局相关分析中，如果全局莫兰指数显著，我们即可认为在该区域上存在空间相关性。但是，我们还是不知道具体在哪儿些地方存在着空间聚集现象。这个时候就需要局部莫兰指数参与帮助说明。
2. 即使全局莫兰指数为0，在局部上也不一定就没有空间聚集现象！(上篇博客中，学生的成绩的例子足以说明，在此不再赘述）

一、公式说明

        还是先从公式入手进行理解，相比全局莫兰指数，局部莫兰指数的计算方式要简洁许多，其计算方式如下：
$$I_i=\frac{Z_i}{S^2}\sum _{j\ne i}^n{w}_{ij}{Z}_j$$
        其中，$Z_i=y_i-\bar{y}$，$Z_j=y_j-\bar{y}$，$S^2=\frac{1}{n}\sum (y_i-\bar{y}{)}^2$，$w_{ij}$为空间权重值，$n$为研究区域上所有地区的总数，$I_i$则代表第$i$个地区的局部莫兰指数。为了方便理解，这里的$y_{i(j)}$还是代表第$i(j)$地区的人均GDP，并将求和号展开（$S^2$总是正的，相当于只是对整个式子进行标准化而已，故这里省略了）：
$$I_i=(y_i-\bar{y})[w_{i1}(y_1-\bar{y})+w_{i2}(y_2-\bar{y})+...w_{i(i-1)}(y_{i-1}-\bar{y})+w_{i(i+1)}(y_{i+1}-\bar{y})+...+w_{in}(y_n-\bar{y})]$$

        从上式不难看出，$I_i$的正负取决于$y_i-\bar{y}$和后面那一坨。前者可反映出第$i$个地区的经济发展水平与整个区域的平均水平之间的高低情况，后者则反映出第$i$个地区的周边地区与整个区域水平之间的高低情况。两个式子都有高低两种可能性，两两组合，共有四种情况。

以表格的方式呈现如下：

$Z_i$	$\sum _{j\ne i}^n{w}_{ij}{Z}_j$	$I_i$	含义
>0	>0	>0	第i个地区经济发展水平高，周边地区发展水平高
<0	<0	>0	第i个地区经济发展水平低，周边地区发展水平低
<0	>0	<0	第i个地区经济发展水平低，周边地区发展水平高
>0	<0	<0	第i个地区经济发展水平高，周边地区发展水平低

关于局部莫兰指数的范围问题在此进行说明：
大部分文献中指出的莫兰指数都是全局莫兰指数，它的范围是-1到1，而局部莫兰指数的范围是没有限制的！详细可参考王庆喜的《区域经济研究实用方法:基于Arcgis,Geoda和R运用》，如下图所示：

二、Moran’I散点图

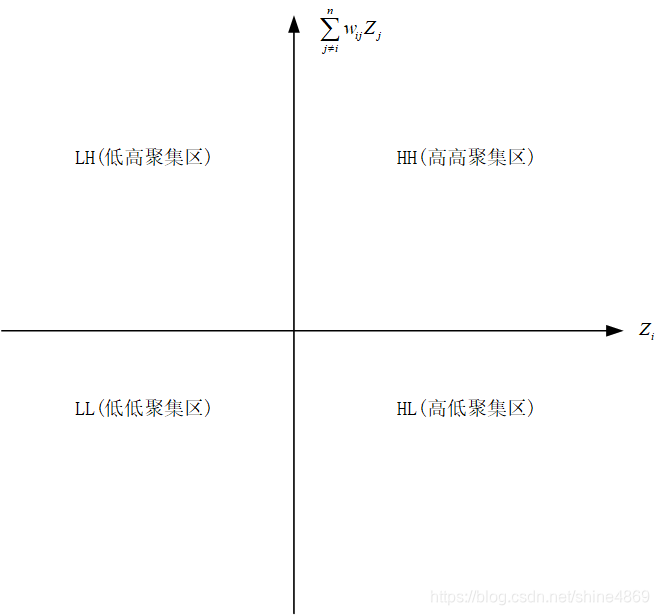
当然，将上表内容以可视化的方式呈现，就得到了Moran’I散点图。以$Z_i$为x轴，$\sum _{j\ne i}^n{w}_{ij}{Z}_j$为y轴，将平面区域划分为四个象限，如下图所示：

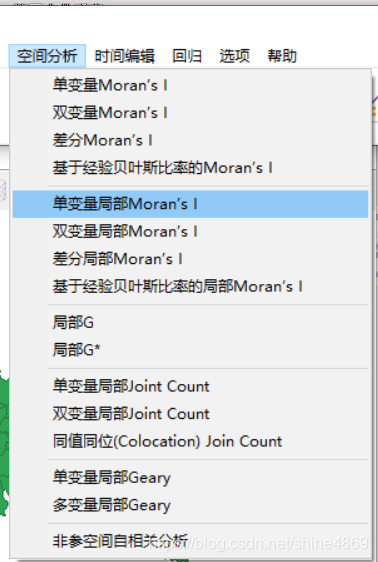
这里还是以2018年人均GDP为基础数据，利用Geoda进行局部相关分析。操作过程如下：
导入空间权重矩阵——空间分析——单变量局部Moran’I分析

选择PGDP2018后，弹出以下对话框，这里我们先选择Moran散点图

细心地小伙伴可能会发现，下面这张图和全局莫兰指数得到的图是一样的！(emm.上面的那个moran’I 是全局莫兰指数，下面这些散点的横纵坐标的乘积就是各个区县的局部莫兰指数。相当于，一张图涵盖了两种指数的信息。

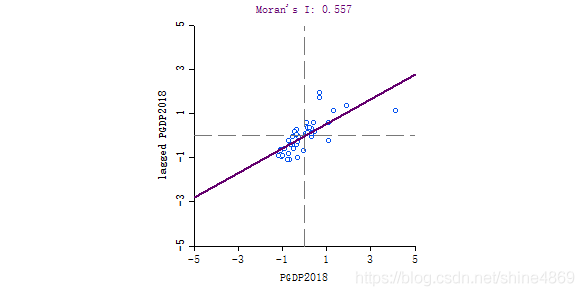
        简单对这张图分析一下：从局部相关的角度来看，第一、三象限的点明显多于第二、四象限的点，即表示"低—低"型和"高—高"型聚集的区县较"高—低"型、"低—高"型的区县更多。更简单地来说，即经济较低(高)的区县在空间上更易聚集。从差异的角度来看，若"低—低"型和"高—高"型区县数量多，即说明此时的空间差异较小。（类比，你胖，周围人也胖，是不是你就胖的不明显啦

顺便提一下，既然全局莫兰指数和局部莫兰指数都称莫兰指数，两者肯定是有关系的，数学公式表达如下：
$$I=\frac{\sum _i{I}_i}{S_0\frac{\sum _i{Z}_i}{n}}$$

更多详细的内容，有兴趣的小伙伴可参考：
Anselin L . Local Indicators of Spatial Association—LISA[J]. Geographical analysis, 1995, 27(2):93-115.

三、LISA聚集图

说到这儿，好像还没说局部莫兰指数怎么检验吧！其实，检验方法一样还是利用Z检验：
$$Z_i=\frac{I_i-E(I_i)}{\sqrt{var(I_i)}}$$
其实，上面那个moran’I散点图并没有对各个区县的局部莫兰指数进行检验，LISA聚集图在就在给定的显著性水平下，对于那些通过显著性检验的区县以地图的方式呈现出来，绘制的LISA聚集图如下：

左图为重庆市区县经济发展水平LISA聚集图,右图为行政区地图

Geoda就这一点不好，没法将区县名显示在LISA聚集图上。(有该需要的可以用Arcgis实现

从上图不难看出，重庆市经济发展水平较高的都聚集在渝西南地区，经济水平较低的大多聚集在渝东北地区，少部分聚集在渝东南地区，此外，"高-低"型和"低-高"型聚集区县并没有呈现出来。(若想更全面地展现经济水平聚集情况，光是人均GDP这一个指标肯定是远远不够的)

以上就是本次分享的全部内容~

这篇关于空间相关分析(三) 局部莫兰指数的理解与计算的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---