分治：循环赛日程表（递归+非递归）

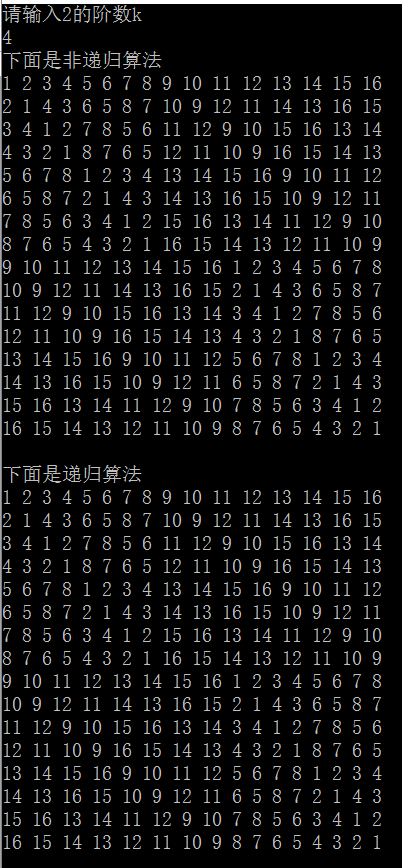
本文主要是介绍分治：循环赛日程表（递归+非递归），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

#include<iostream>
#include<vector>
#include<iterator>
#include<algorithm>
#include<stdio.h>
#include<math.h>
using namespace std;
int a[100][100];/*循环赛日程表的全局变量*/
void copy(int tox,int toy,int fromx,int fromy,int r)/*是一个copy函数，目的是把以r为长度的正方形范围从点from到点to*/
{for(int i=0;i<r;i++)for(int j=0;j<r;j++)a[tox+i][toy+j]=a[fromx+i][fromy+j];
}
void Table_digui(int a[][100],int r,int l,int k)/*递归算法*/
{if(k==1)                       /*如果就一个当然就直接返回啦*/return;Table_digui(a,r,l,k/2);        /*填充左上角*/Table_digui(a,r+(k/2),l,k/2);  /*填充左下角*/copy(r,l,r+k/2,l+k/2,k/2);     /*从左上角拷贝到右下角*/copy(r+k/2,l,r,l+k/2,k/2);     /*从左下角拷贝到右上角*/
}
void Table_feidigui(int k) /*非递归算法*/
{int n=pow(2,k);for(int i=0;i<n;i++) /*第一列初始化*/a[i][0]=i+1;for(int r=2;r<=n;r*=2) /*如果要填充整个表，要有k趟，每一趟的步长为2^i(i=1,2,...k)*/for(int i=0;i<n;i+=r){ /*针对某一趟，假设这趟步长为r，则需要复制正方形的边长为r的一半*/int w=r/2;copy(i+w,w,i,0,w);copy(i,w,i+w,0,w);}
}
void print(int a[][100],int n)  /*输出整个表*/
{for(int i=0;i<n;i++)for(int j=0;j<n;j++){cout<<a[i][j]<<" ";if(j==n-1)puts("");}
}int main()
{int k,n;cout<<"请输入2的阶数k"<<endl;cin>>k;n=pow(2,k);cout<<"下面是非递归算法"<<endl;Table_feidigui(k);print(a,n);for(int i=0;i<n;i++)a[i][0]=i+1;puts("");cout<<"下面是递归算法"<<endl;Table_digui(a,0,0,n);print(a,n);
}