本文主要是介绍Python---函数递归---练习:猴子吃桃问题(本文以递归算法 解法为主),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
相关链接:Python---函数递归---练习:斐波那契数列(本文以递归算法为主)-CSDN博客
案例:猴子吃桃问题
猴子吃桃问题。猴子第1天摘下若干个桃子,当即吃了一半,还不过瘾,又多吃了一个。第2天早上又将剩下的桃子吃掉一半,又多吃了一个。以后每天早上都吃了前一天剩下的一半另加一个。到第10天早上想再吃时,就只剩下一个桃子了。求第1天共摘了多少个桃子
思考:一步步来

第一步:确定函数主要要完成什么功能,需要传递哪些参数,确认调用方式
def f(n):
# 编写递归代码
# 调用f函数
print(f(1))
第二步:编写递归的结束条件(出口)
# 第一步:确定函数功能
def f(n):
# 第二步:编写递归结束条件(出口)
if n == 10:
return 1
# 调用函数
print(f(1))
第三步:找出与这个问题相等的等式关系
看要求
猴子第1天摘下若干个桃子,当即吃了一半,还不过瘾,又多吃了一个。第2天早上又将剩下的桃子吃掉一半,又多吃了一个。以后每天早上都吃了前一天剩下的一半另加一个。到第10天早上想再吃时,就只剩下一个桃子了。求第1天共摘了多少个桃子。
求桃子的剩余数量?假设法:假设有10个桃子---------自己开始列举
第1天,10个桃子吃一半,10/2 = 5 + 1 = 6 # + 1 是 还不过瘾又多吃了一个,总共吃6个,剩4个
第2天,4个桃子吃一半,4/2 = 2 + 1 = 3 # + 1 是 还不过瘾又多吃了一个,总共吃3个,剩1个
第3天,再想吃剩1个
第n天,总剩余桃子的数量 = (第(n+1)天桃子的剩余桃子的数量 + 1) * 2
# 这里是反推,计算桃子数量-----每天剩余桃子的总数,都是之后一天桃子的总数。
求总的第1天共摘了多少个桃子,那么就可以从第二天初始桃子的总数进行反推,是一开始是一半,除以2,那么就乘以2,再加上1---------就是第一天桃子的总数。
可以把这些情景,当做自己买水果,代入思考,就能很快假设出来。
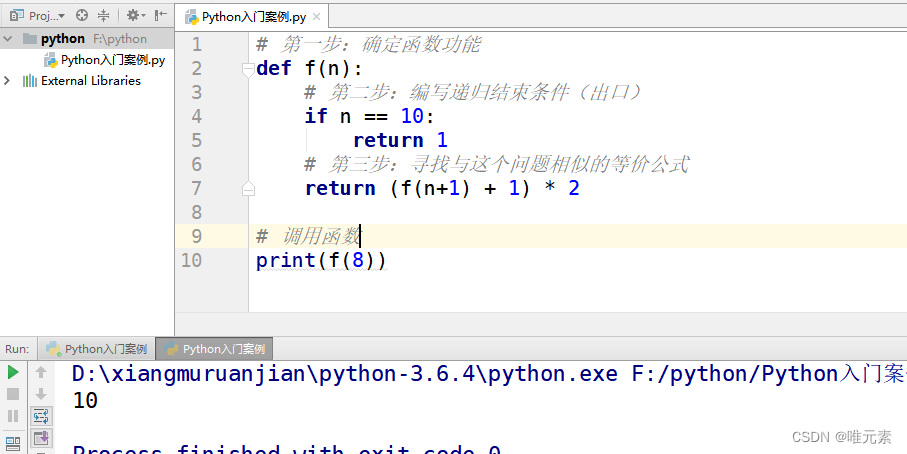
# 第一步:确定函数功能 def f(n):# 第二步:编写递归结束条件(出口)if n == 10:return 1# 第三步:寻找与这个问题相似的等价公式return (f(n+1) + 1) * 2# 调用函数 print(f(8))
这篇关于Python---函数递归---练习:猴子吃桃问题(本文以递归算法 解法为主)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






