本文主要是介绍分形三维快速入门,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
打开一个简单模型文件
本章内容不需要太深的代码基础。完成之后,您就能够掌握使用fractal3D api在网页上渲染一个简单的obj/gltf/fbx/dae/3mf/gcode等文件的方法。
一个静态页面
假设您已经创建好一个html文件
引入脚本
在html文件的开头引入fractal 3d脚本地址,当网页启动之后,浏览器将会自动向分形三维服务器请求这个脚本文件
<head>
<script src="https://cdn.everxyz.com/everapi/stable/everapi@v4.2.5.js" defer="" data-nscript="beforeInteractive"></script>
</head>添加组件
向页面中添加 fractal 3D 组件,并根据您的需要调整渲染窗口的长宽
<ever-3d id="hello" width="800px" height='600px' />初始化 fractal 3D
window.EverAPI.login('<APP_ID>', '<APP_KEY>');请注意;此处的 APP_ID 与 APP_KEY是一组密钥, 需要提前向分形三维 申请。
输入模型文件的路径
假设你有一个名为asset的obj文件,并且放在和html文件同层的一个名为assets的文件夹下,形如:
instance.openFiles([{filename:"asset.obj",url:"assets/asset.obj"}])详细源码
<!DOCTYPE html>
<html><head><meta charset="utf-8"><script src='https://cdn.everxyz.com/everapi/stable/everapi@v4.2.5.js'></script>
</head><body><!-- filename中需要正确的文件后缀名 --><!-- 这里把文件放到和index.html同一个文件夹中,然后把文件名(包括后缀)同时填入 filename 和 url 中即可 --><!-- 例如这里,我的文件夹中有一个 asset.obj 文件,所以我填入的是 assets/asset.obj --><!-- 其他不用改,我们就可以在网页显示 3d 文件了 --><ever-3d id="hello" width="800px" height='600px' /><script>let instance = window.EverAPI.getInstanceById('hello');// 此处的 appid 与 appkey 需要填入你在 fractal 3d 申请得到的// 下面的 appid 与 appkey 只在 localhost:9000 可用window.EverAPI.login('<APP_ID>', '<APP_KEY>');instance.openFiles([{ filename: "asset.obj", url: "assets/asset.obj" }]);</script>
</body></html>运行方法-Mac/Linux
在html文件所在的路径下,打开命令行工具,执行以下命令
http-server -p 9000我们推荐大家使用Node.js中的http-server模块。Mac/Linux上安装Node.js的方法请参考这里。
当命令行界面出现类似的信息,就说明启动成功了
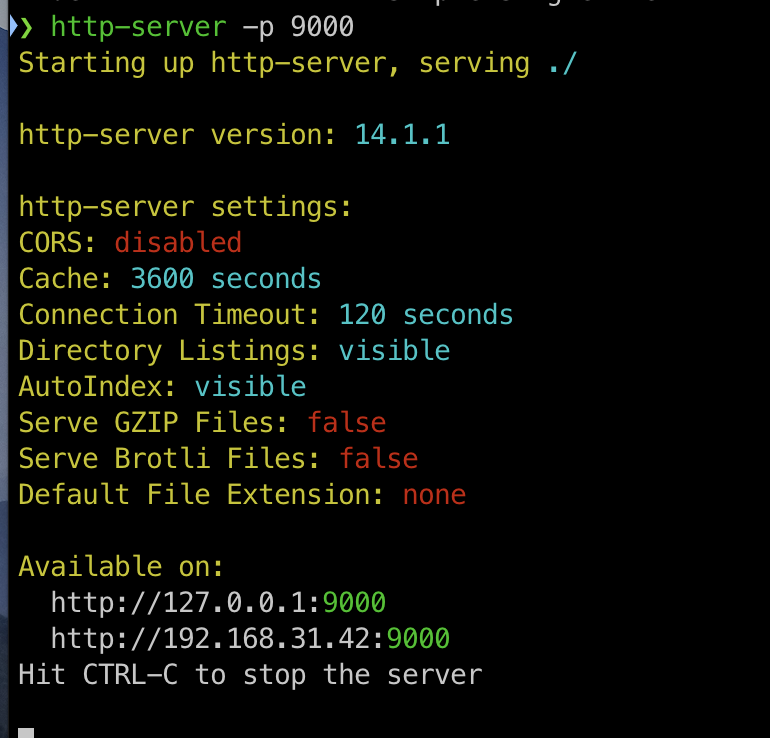
打开浏览器,在地址栏中输入“localhost:9000",敲击回车就可以看到模型浏览界面了
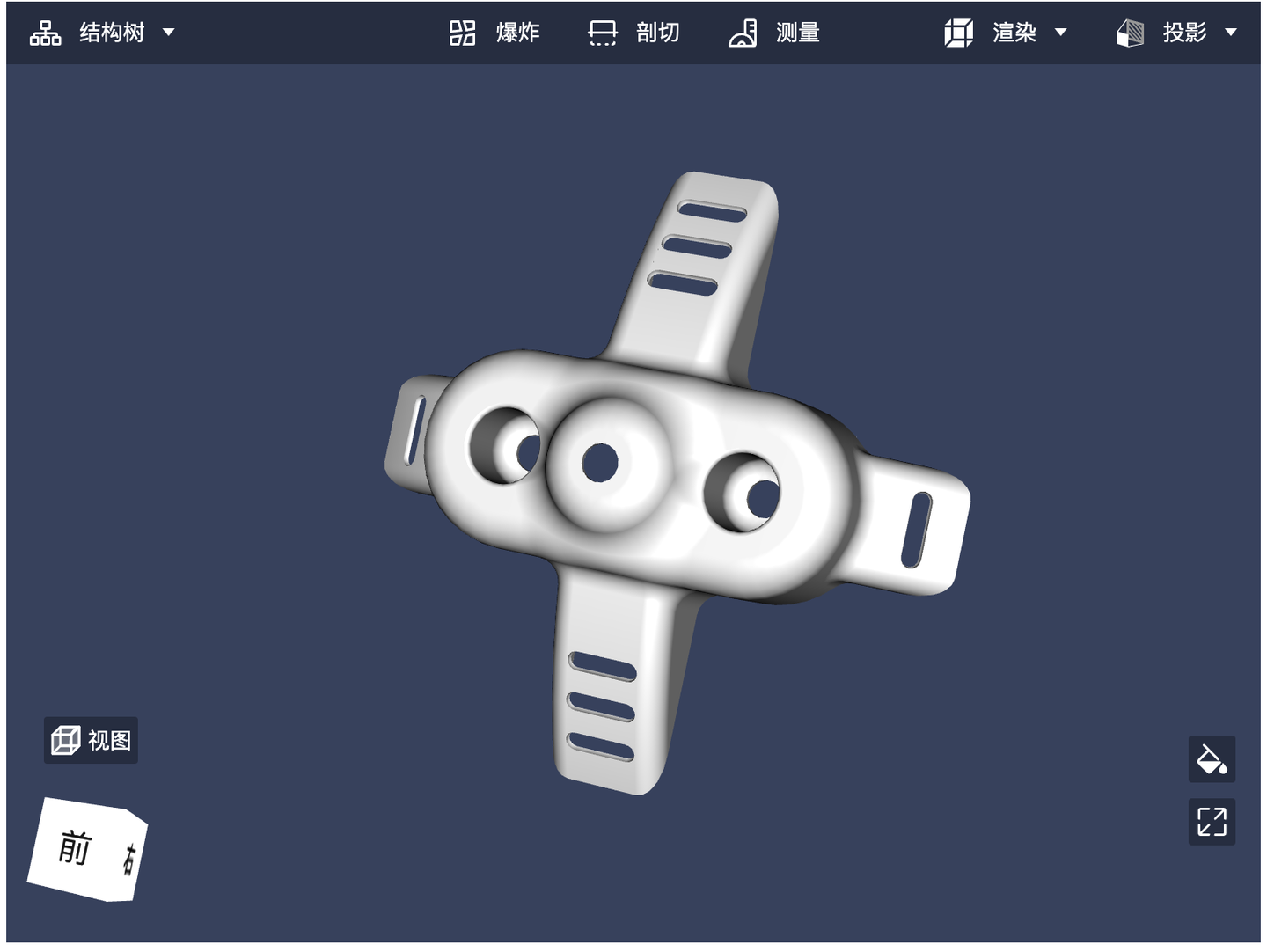
运行方法-windows
windows系统安装Node.js比较复杂,为了方便大家快速体验demo,我们为大家提供了一个http-server的可执行程序。(http-server.exe)
在html文件所在的路径下,运行powershell/CMD/windows terminal,并执行以下命令
.\http-server.exe -i -p 9000其余的操作和Mac/Linux一致 如果想改用自己的模型文件,使用文本编辑器打开 index.html, 将文件名和url替换为您的文件就可以了。
完整示例
参考Demos中的simple-singlefile.html
这篇关于分形三维快速入门的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







