本文主要是介绍【Matlab】如何快速入门一项新技能-以Matlab/Simulink入门为例,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1. 引言
2. 背景
3. 快速学习并完成开发
3.1 了解需求,知道要干什么
3.2 了解Matlab/Simulink基本功能
第一步,查看Matlab的中文网站中文网站https://www.ilovematlab.cn/resources/对Matlab/Simulink有了一个初步认识。
3.3 实现一个最简单模块,走完完整的开发流程
3.4 实现复杂功能,记录问题点
3.5 系统的学习Matlab基础,解决一些概念疑惑
3.6 未来可期,需要系统学习
4. 抽象总结,如何快速的入门一项新技术
1. 引言
现在各种新的技术或工具层出不穷,我们在工作中难免会遇到在短时间内学习一项新技术或工具并解决实际问题的情况,这就需要我们快速入门并上手工作。笔者在项目开发的过程中就遇到这样的情况,成功在短时间内入门一项新技术并完成开发任务,这里记录下自己学习和开发过程,希望对读者有一定的启发。
2. 背景
笔者目前正在开发车辆域控制器项目,开发流程是自顶向下,ASW(Application Software)开发工具用的是Matlab/Simulink,开发任务是在一周内完成ET1阶段的车门锁控制系统开发。但是,笔者的Matlab/Simulink知识是0基础,这就需要在短时间内学会使用Matlab/Simulink并完成开发任务。

3. 快速学习并完成开发
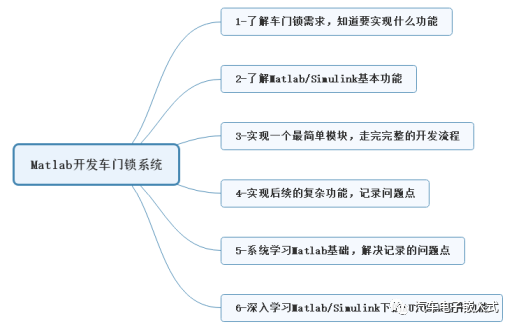
3.1 了解需求,知道要干什么
车门锁系统感知各种解闭锁触发事件(遥控钥匙解闭锁,中控开关解闭锁,机械钥匙解闭锁等),控制门锁电机的解锁和闭锁,同时反馈四门开关及车门锁反馈状态。
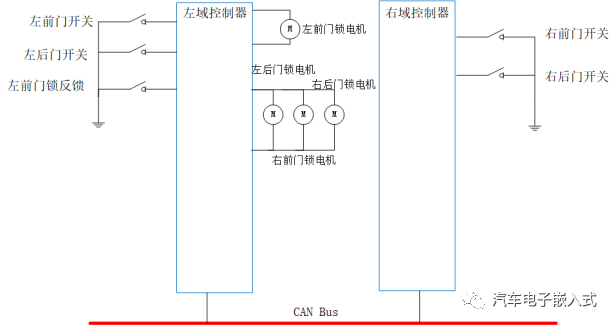
3.2 了解Matlab/Simulink基本功能
第一步,查看Matlab的中文网站中文网站https://www.ilovematlab.cn/resources/对Matlab/Simulink有了一个初步认识。
第二步,查看了一个StateFlow的学习文档,了解Stateflow的基本功能。
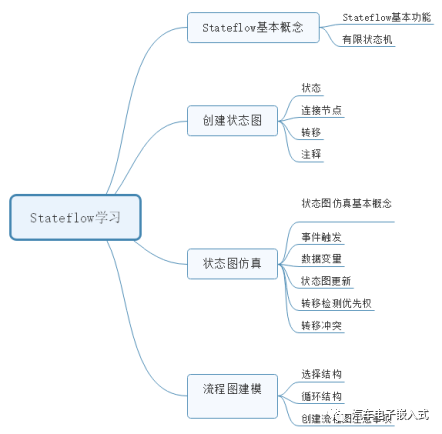
3.3 实现一个最简单模块,走完完整的开发流程
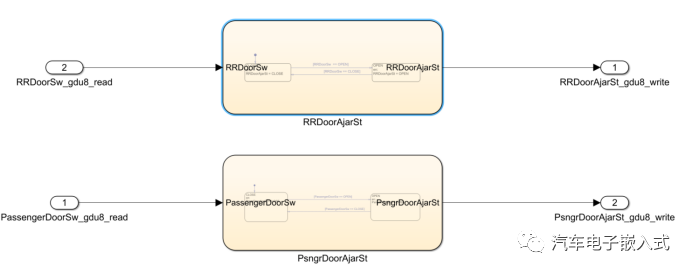
根据实际需求,右域控制器的功能最简单,开始摸索着模型开发。其中咨询了同事很多基本的问题,有人问真好。完成了右域控制器的模型开发。
模型开发:


数据管理:
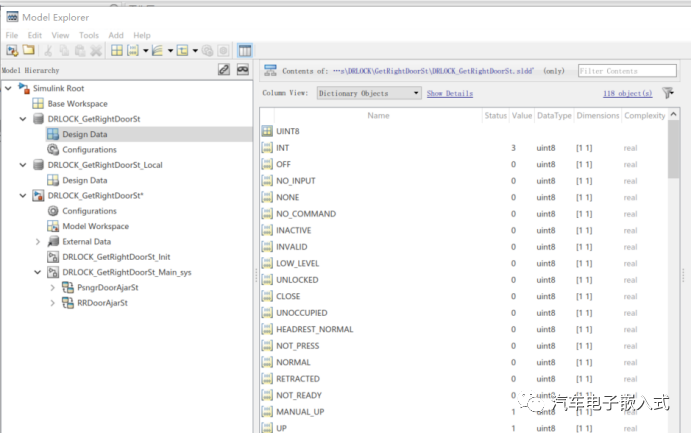
MIL测试:
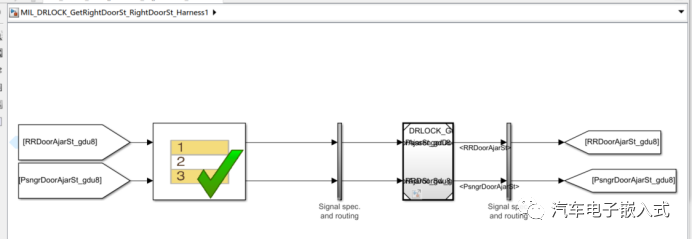
代码生成:
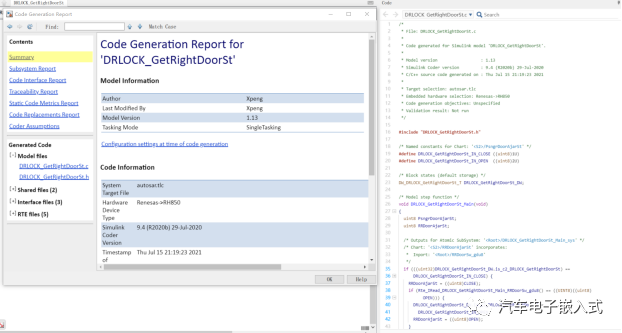
这样就走完了一个比较完整的开发流程,同时做了以下的一些学习笔记。
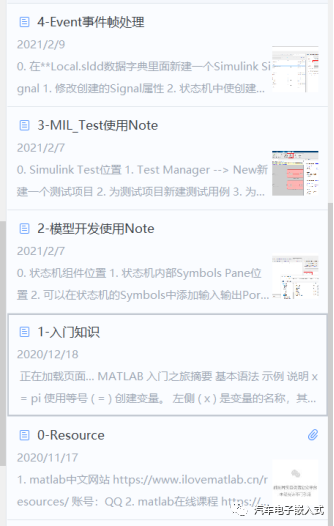
到这一步就差不多有点Matlab/Simulink开发的feeling了。接下来一鼓作气实现复杂一点的功能。
3.4 实现复杂功能,记录问题点
车门锁比较复杂的功能就是对四个车门锁电机的花式控制。
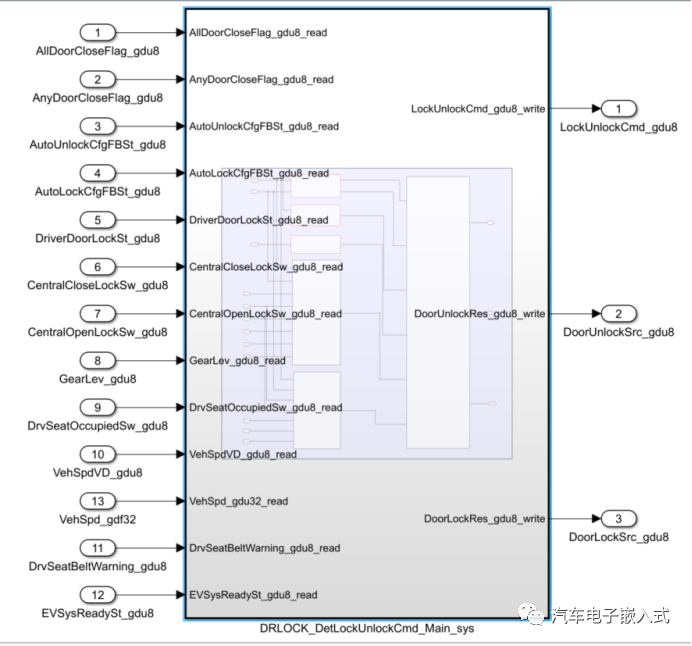
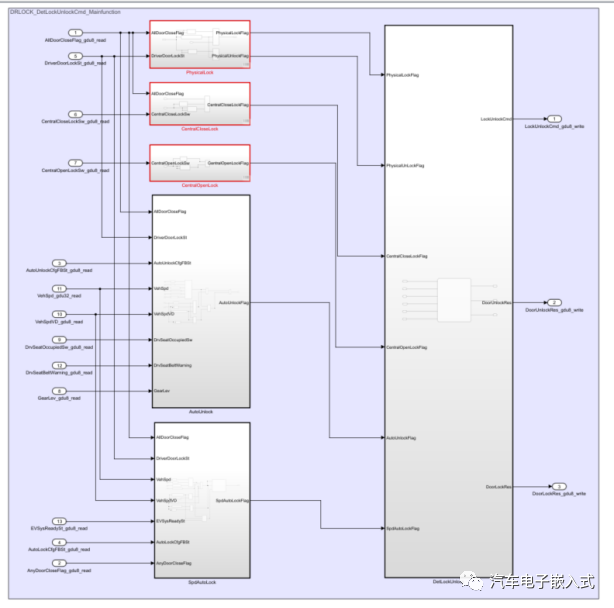
记录问题:不管是再简单基础的问题,不懂就是不懂,都要搞清楚。
-- 1. 模型配置在哪里配置?怎么合理的配置?
-- 2. 怎么配置符合AUTOSAR规范的模型接口?
-- 3. 怎么通过ARXML文件生成AUTOSAR架构的模型?
-- 4. 怎么配置可以修改代码的生成风格?
-- 5. 模型配置,数据管理,模型验证怎么根据项目来配置?
3.5 系统的学习Matlab基础,解决一些概念疑惑
主要学习MATHWORK公司的一个官方基础视频,视频地址:
https://www.bilibili.com/video/BV1Kz4y1r7ep?p=1
并做了以下笔记:
3.6 未来可期,需要系统学习
笔者主要做AUTOSAR相关的开发,所以需要系统的学习Matlab/Simulink/AUSTSAR Component这个组件。
资料已经准备好:

4. 抽象总结,如何快速的入门一项新技术
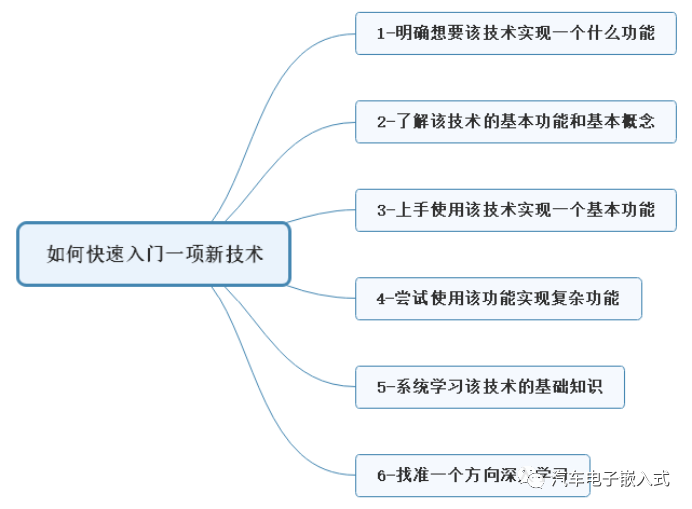
带有目的的去学习,效率要高很多。当我们要学习一项新技术/工具的时候,先明确知道自己想要实现什么功能,然后带着目的去了解该技术/工具的基本功能和概念,心中大概有点想法的时候就可以去尝试实现一些简单模块的功能了。在实现简单功能的过程中遇到问题解决问题,并记录下不懂或者不会的地方,由简到繁实现整个功能。再带着问题去系统的学习该技术的基础知识,尝试解决完所有的问题。最后找准一个应用方向,深入学习,这样就可以一步一步成为这个方向的专家了。
这篇关于【Matlab】如何快速入门一项新技能-以Matlab/Simulink入门为例的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





