本文主要是介绍有权图的最短路径算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
单源最短路径问题
Dijkstra算法
原理
获得最短路径长度的Dijkstra代码实现
时间复杂度
算法优化
优先队列优化后的代码实现
时间复杂度
可以具体获得最短路径的Dijkstra代码实现
Bellman-Ford算法
原理
代码实现
Floyed算法
原理
代码实现
单源最短路径问题
我们的起始点是固定点,从起始点出发到达其他各顶点的最短路径。
Dijkstra算法
此算法不能处理负权边,由于大量的应用不依赖负权边,所以这个算法有非常广泛的应用。
原理 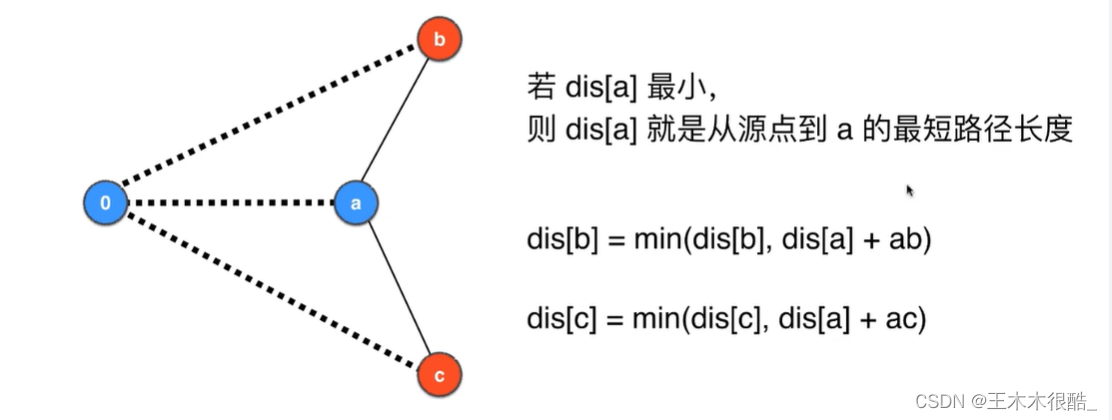

获得最短路径长度的Dijkstra代码实现
import java.util.Arrays;public class Dijkstra {private WeightedGraph G;private int s;//源点sprivate int[] dis;//整型数组表示源点s到某个顶点的距离private boolean[] visited;//找到还没确定最短距离的顶点public Dijkstra(WeightedGraph G, int s){this.G = G;G.validateVertex(s);//验证合法性this.s = s;dis = new int[G.V()];Arrays.fill(dis, Integer.MAX_VALUE);//赋初值dis[s] = 0;//赋初值为0visited = new boolean[G.V()];while(true){//循环的第一轮找到的必是源点sint cur = -1;//最小的dis值对应的顶点是谁 int curdis = Integer.MAX_VALUE;//当前找到的最小的dis值for(int v = 0; v < G.V(); v ++)if(!visited[v] && dis[v] < curdis){curdis = dis[v];cur = v;}if(cur == -1) break;//代表当前所有的顶点都访问过了,可以退出咯visited[cur] = true;//哪些顶点的dis值已经求出来了for(int w: G.adj(cur))if(!visited[w]){if(dis[cur] + G.getWeight(cur, w) < dis[w])dis[w] = dis[cur] + G.getWeight(cur, w);}}}public boolean isConnectedTo(int v){//判断顶点和源点的连通性G.validateVertex(v);return visited[v];}public int distTo(int v){//从源点s到顶点v对应的最短路径的长度G.validateVertex(v);return dis[v];}static public void main(String[] args){WeightedGraph g = new WeightedGraph("g.txt");Dijkstra dij = new Dijkstra(g, 0);for(int v = 0; v < g.V(); v ++)System.out.print(dij.distTo(v) + " ");System.out.println();}
}时间复杂度
算法优化

我们可以用优先队列获得v这个顶点对应的dis值,不再是v这个顶点序号的最小值了。我们的优先队列取出来的是顶点的序号,但比较起来是比较的dis值。
优先队列优化后的代码实现
import java.util.Arrays;
import java.util.PriorityQueue;public class Dijkstra {private WeightedGraph G;private int s;private int[] dis;private boolean[] visited;private class Node implements Comparable<Node>{public int v, dis;public Node(int v, int dis){this.v = v;this.dis = dis;}@Overridepublic int compareTo(Node another){return dis - another.dis;}}public Dijkstra(WeightedGraph G, int s){this.G = G;G.validateVertex(s);this.s = s;dis = new int[G.V()];Arrays.fill(dis, Integer.MAX_VALUE);dis[s] = 0;visited = new boolean[G.V()];PriorityQueue<Node> pq = new PriorityQueue<Node>();pq.add(new Node(s, 0));while(!pq.isEmpty()){int cur = pq.remove().v;if(visited[cur]) continue;visited[cur] = true;for(int w: G.adj(cur))if(!visited[w]){if(dis[cur] + G.getWeight(cur, w) < dis[w]){dis[w] = dis[cur] + G.getWeight(cur, w);pq.add(new Node(w, dis[w]));}}}}public boolean isConnectedTo(int v){G.validateVertex(v);return visited[v];}public int distTo(int v){G.validateVertex(v);return dis[v];}static public void main(String[] args){WeightedGraph g = new WeightedGraph("g.txt");Dijkstra dij = new Dijkstra(g, 0);for(int v = 0; v < g.V(); v ++)System.out.print(dij.distTo(v) + " ");System.out.println();}
}时间复杂度

可以具体获得最短路径的Dijkstra代码实现
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.PriorityQueue;public class Dijkstra {private WeightedGraph G;private int s;private int[] dis;private boolean[] visited;private int[] pre;private class Node implements Comparable<Node>{public int v, dis;public Node(int v, int dis){this.v = v;this.dis = dis;}@Overridepublic int compareTo(Node another){return dis - another.dis;}}public Dijkstra(WeightedGraph G, int s){this.G = G;G.validateVertex(s);this.s = s;dis = new int[G.V()];Arrays.fill(dis, Integer.MAX_VALUE);pre = new int[G.V()];Arrays.fill(pre, -1);dis[s] = 0;pre[s] = s;visited = new boolean[G.V()];PriorityQueue<Node> pq = new PriorityQueue<Node>();pq.add(new Node(s, 0));while(!pq.isEmpty()){int cur = pq.remove().v;if(visited[cur]) continue;visited[cur] = true;for(int w: G.adj(cur))if(!visited[w]){if(dis[cur] + G.getWeight(cur, w) < dis[w]){dis[w] = dis[cur] + G.getWeight(cur, w);pq.add(new Node(w, dis[w]));pre[w] = cur;}}}}public boolean isConnectedTo(int v){G.validateVertex(v);return visited[v];}public int distTo(int v){G.validateVertex(v);return dis[v];}public Iterable<Integer> path(int t){ArrayList<Integer> res = new ArrayList<>();if(!isConnectedTo(t)) return res;int cur = t;while(cur != s){res.add(cur);cur = pre[cur];}res.add(s);Collections.reverse(res);return res;}static public void main(String[] args){WeightedGraph g = new WeightedGraph("g.txt");Dijkstra dij = new Dijkstra(g, 0);for(int v = 0; v < g.V(); v ++)System.out.print(dij.distTo(v) + " ");System.out.println();System.out.println(dij.path(3));}
}Bellman-Ford算法
原理
松弛操作有方向性,相当于拐个弯到达某个端点是不是比直接到达某个端点更近。此算法在有向图无向图也成立。




代码实现
import java.util.Arrays;public class BellmanFord {private WeightedGraph G;private int s;private int[] dis;private boolean hasNegCycle = false;public BellmanFord(WeightedGraph G, int s){this.G = G;G.validateVertex(s);this.s = s;dis = new int[G.V()];Arrays.fill(dis, Integer.MAX_VALUE);dis[s] = 0;for(int pass = 1; pass < G.V(); pass ++){for(int v = 0; v < G.V(); v ++)for(int w: G.adj(v))if(dis[v] != Integer.MAX_VALUE &&dis[v] + G.getWeight(v, w) < dis[w])dis[w] = dis[v] + G.getWeight(v, w);}for(int v = 0; v < G.V(); v ++)for(int w : G.adj(v))if(dis[v] != Integer.MAX_VALUE &&dis[v] + G.getWeight(v, w) < dis[w])hasNegCycle = true;}public boolean hasNegativeCycle(){return hasNegCycle;}public boolean isConnectedTo(int v){G.validateVertex(v);return dis[v] != Integer.MAX_VALUE;}public int distTo(int v){G.validateVertex(v);if(hasNegCycle) throw new RuntimeException("exist negative cycle.");return dis[v];}static public void main(String[] args){WeightedGraph g = new WeightedGraph("g.txt");BellmanFord bf = new BellmanFord(g, 0);if(!bf.hasNegativeCycle()){for(int v = 0; v < g.V(); v ++)System.out.print(bf.distTo(v) + " ");System.out.println();}elseSystem.out.println("exist negative cycle.");WeightedGraph g2 = new WeightedGraph("g2.txt");BellmanFord bf2 = new BellmanFord(g2, 0);if(!bf2.hasNegativeCycle()){for(int v = 0; v < g2.V(); v ++)System.out.print(bf2.distTo(v) + " ");System.out.println();}elseSystem.out.println("exist negative cycle.");}
}Floyed算法
原理

可以包含负权边,也可以包含负权环。
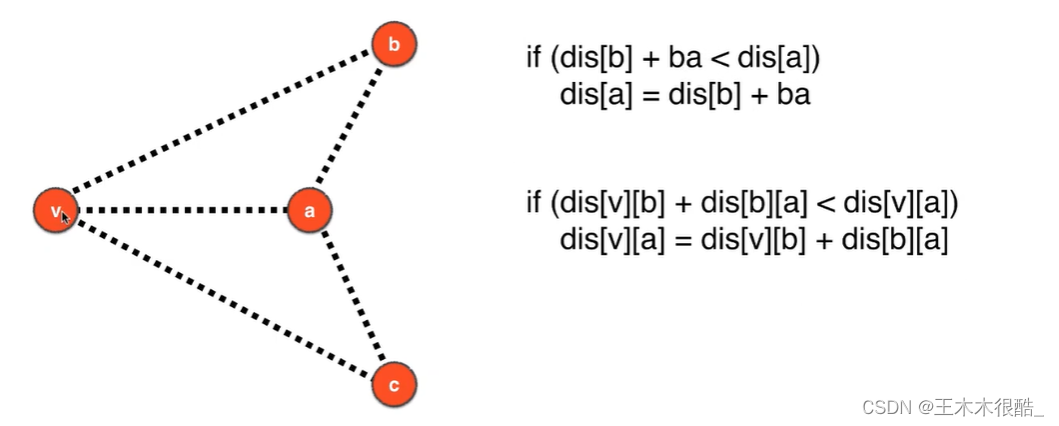
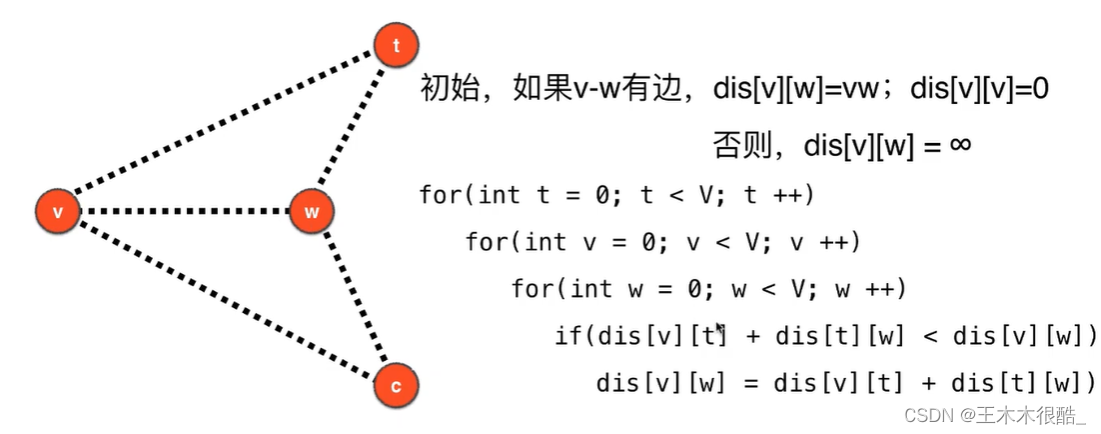
代码实现
import java.util.Arrays;public class Floyed {private WeightedGraph G;private int[][] dis;private boolean hasNegCycle = false;public Floyed(WeightedGraph G){this.G = G;dis = new int[G.V()][G.V()];for(int v = 0; v < G.V(); v ++)Arrays.fill(dis[v], Integer.MAX_VALUE);for(int v = 0; v < G.V(); v ++){dis[v][v] = 0;for(int w: G.adj(v))dis[v][w] = G.getWeight(v, w);}for(int t = 0; t < G.V(); t ++)for(int v = 0; v < G.V(); v ++)for(int w = 0; w < G.V(); w ++)if(dis[v][t] != Integer.MAX_VALUE && dis[t][w] != Integer.MAX_VALUE&& dis[v][t] + dis[t][w] < dis[v][w])dis[v][w] = dis[v][t] + dis[t][w];for(int v = 0; v < G.V(); v ++)if(dis[v][v] < 0)hasNegCycle = true;}public boolean hasNegativeCycle(){return hasNegCycle;}public boolean isConnectedTo(int v, int w){G.validateVertex(v);G.validateVertex(w);return dis[v][w] != Integer.MAX_VALUE;}public int distTo(int v, int w){G.validateVertex(v);G.validateVertex(w);return dis[v][w];}static public void main(String[] args){WeightedGraph g = new WeightedGraph("g.txt");Floyed floyed = new Floyed(g);if(!floyed.hasNegativeCycle()){for(int v = 0; v < g.V(); v ++){for(int w = 0; w < g.V(); w ++)System.out.print(floyed.distTo(v, w) + " ");System.out.println();}}elseSystem.out.println("exist negative cycle.");WeightedGraph g2 = new WeightedGraph("g2.txt");Floyed floyed2 = new Floyed(g2);if(!floyed2.hasNegativeCycle()){for(int v = 0; v < g.V(); v ++){for(int w = 0; w < g.V(); w ++)System.out.print(floyed2.distTo(v, w) + " ");System.out.println();}}elseSystem.out.println("exist negative cycle.");}
}这篇关于有权图的最短路径算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





