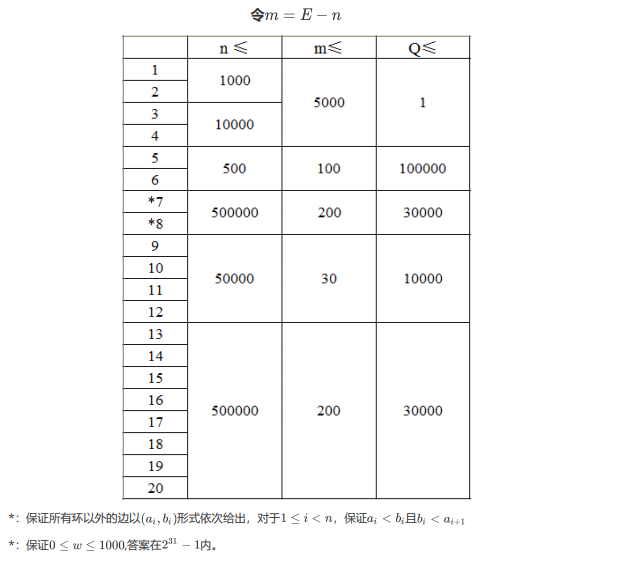
题面

分析
题上悄悄的隐藏了一个,这是一个环的条件,这个一定得看出来。

就是这句话。所以不要把它当成基环树之类的了。。
前4个点,最短路随便跑吧。我还是不长教训用的spfa,人品太好,切勿效仿!!
后面的分,发现除了环上的边,其余多余的边其实很少,最多只有200条,意思是最多只有400个点间有边。
既然求最短路,何不把这200条边的图建出来,然后对于非环边跑floyd,再结合环上的边处理最短路。
我们可以找到离u和v最近的两个点,它们分别是u1,u2,v1,v1
无非这几种情况 u->v u->u1->v1->v u->u1->v2->v u->u2->v1->v u->u2->v2->v
代码是真不好写。。。
代码
- #include<bits/stdc++.h>
- using namespace std;
- #define M 404
- #define N 500050
- #define INF 0x3f3f3f3f
- int n,m,Q,cnt,tot,mpn,tmpn;
- int dis[M][M];
- int d[N],vis[N],first[N],nt[N],eu[N],ev[N],ew[N],mp[N],tmp[N];
- struct email
- {
- int u,v,w;
- int nxt;
- }e[N*4];
- struct query
- {
- int st,ed;
- }a[N];
- template<class T>
- void read(T &x)
- {
- x = 0;
- static char c = getchar();
- while(c < '0' || c > '9') c = getchar();
- while(c >= '0' && c <= '9')
- x = x * 10 + c - '0', c = getchar();
- }
- inline void add(int u,int v,int w)
- {
- e[cnt].nxt=first[u];first[u]=cnt;
- e[cnt].u=u;e[cnt].v=v;e[cnt].w=w;++cnt;
- }
- queue<int>q;
- void spfa(int x)
- {
- q.push(x);
- for(int i=1;i<=n;i++)d[i]=INF;
- d[x]=0;vis[x]=1;
- while(!q.empty())
- {
- int u=q.front();q.pop();vis[u]=0;
- for(int i=first[u];i;i=e[i].nxt)
- {
- int v=e[i].v,w=e[i].w;
- if(d[v]>d[u]+w)
- {
- d[v]=d[u]+w;
- if(!vis[v])
- {q.push(v);vis[v]=1;}
- }
- }
- }
- }
- int cir(int u,int v)
- {
- if(u==v)return 0;
- if(u>v)swap(u,v);
- v--;
- int x=nt[v]-(u?nt[u-1]:0);
- return min(x,nt[n-1]-x);
- }
- int main()
- {
- read(n);read(m);read(Q);
- if(Q==1)
- {
- for(int i=1;i<=m;i++)
- {
- int u,v,w;
- read(u);u--;read(v);v--;read(w);
- add(u,v,w);add(v,u,w);
- }
- int s,t;
- read(s);s--;read(t);t--;
- spfa(s);printf("%d\n",d[t]);
- return 0;
- }
- memset(nt,0x3f,sizeof(nt));
- for(int i=1;i<=m;i++)
- {
- int u,v,w;
- read(u);u--;read(v);v--;read(w);
- if(v==(u+1)%n)nt[u]=min(nt[u],w);
- else if(u==(v+1)%n)nt[v]=min(nt[v],w);
- else
- {
- eu[tot]=u,ev[tot]=v;ew[tot++]=w;
- tmp[tmpn++]=u,tmp[tmpn++]=v;
- }
- }
- for(int i=1;i<n;i++)nt[i]+=nt[i-1];
- sort(tmp,tmp+tmpn);
- mp[mpn++]=tmp[0];
- for(int i=1;i<tmpn;i++)
- if(tmp[i]!=tmp[i-1])
- mp[mpn++]=tmp[i];
- for(int i=0;i<mpn;i++)
- for(int j=0;j<mpn;j++)
- dis[i][j]=cir(mp[i],mp[j]);
- for(int i=0;i<tot;i++)
- {
- int u=lower_bound(mp,mp+mpn,eu[i])-mp;
- int v=lower_bound(mp,mp+mpn,ev[i])-mp;
- dis[u][v]=dis[v][u]=min(dis[u][v],ew[i]);
- }
- for(int k=0;k<mpn;k++)
- for(int i=0;i<mpn;i++)
- for(int j=0;j<mpn;j++)
- dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
- for(int i=1;i<=Q;i++)
- {
- int u,v;
- read(u);u--;read(v);v--;
- int u1=(upper_bound(mp,mp+mpn,u)-mp)%mpn,u2=(u1-1+mpn)%mpn;
- int v1=(upper_bound(mp,mp+mpn,v)-mp)%mpn,v2=(v1-1+mpn)%mpn;
- int ans=cir(u,v);
- ans=min(ans,cir(u,mp[u1])+cir(mp[v1],v)+dis[u1][v1]);
- ans=min(ans,cir(u,mp[u1])+cir(mp[v2],v)+dis[u1][v2]);
- ans=min(ans,cir(u,mp[u2])+cir(mp[v1],v)+dis[u2][v1]);
- ans=min(ans,cir(u,mp[u2])+cir(mp[v2],v)+dis[u2][v2]);
- printf("%d\n",ans);
- }
- return 0;
- }








