▎(一个没有用处的)前言
为什么这次题解特意写明题号呢?因为我发现了这样的事情:
所以不要混了,想看P1714题解的同志们可以圆润的滚开了。
好了,不说没用的了,切入正题:
▎题目
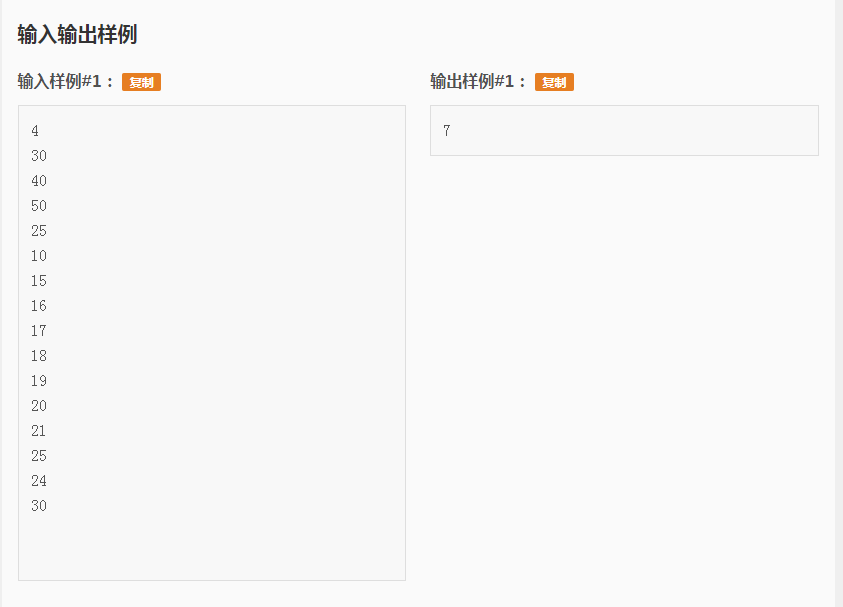
题目及测评链接:戳这里
▎前置技能
贪心(点击查看)、搜索(点击查看)、剪枝(点击查看)、二分(点击查看)。
▎解析
这道题看起来令人不知所措,不知道的东西太多了,到底如何分配,一看就是要用到搜索的题,但怕是连搜索也很难写了。
我们按照顺序一点一点的想:
首先,我们不知道如何分配,只能像无头苍蝇一样到处乱撞,所以我们可以先假设有多少人可以被满足,然后再实际用搜索检验一下这个假设是否可以成功,如果能行,那么增加这个假设的人数,继续试验;如果不行,那么就减少这个假设的人数,继续试验。
这就和原来不一样了,现在是有目标的,而且可以充分保证正确率。现在大致的思路就是这样的:

这就是我们的整体大思路,但是这样的方法时间复杂度显然是不可以的,我们需要一定的优化,其实优化是很简单的,只要有点生活常识就行:
①一块蛋糕一定能满足更多的嘴小的人,而不是更多嘴大的人。所以,贪心的想:如果将人按照嘴的大小排序,是不是更好呢?
②题目中明确规定不能将两块蛋糕拼起来,所以,如果一个人嘴大到连最大的蛋糕都无法满足,那就可以把他踢出去了,那么就不再考虑这个人了,因为无论如何都满足不了。所以依次(从大到小)把嘴大于最大的蛋糕的人全部排除掉,减少搜索判断次数,就可以起到优化的效果了。
③我们要先假设能满足的人数,那么该怎样假设呢?总得有个顺序吧,从小到大?从大到小?显然多一次假设就会多一次搜索,那么减少假设次数便是一个关键。于是我们便想到了二分,如果使用二分的话,就可以大大减少假设次数。
④剪枝优化1:每一次试探中蛋糕都会有所浪费,怎样判别是否浪费呢?显然,如果一块蛋糕分给一个人一部分后,剩下的连嘴最小的人都满足不了了,那么就一定浪费了。如果蛋糕总量减去浪费的蛋糕量(即这种方法剩下的蛋糕总量)比前n个人的总需求量还小,那么就说明无论如何都满足不了这n个人了,应该立即返回0,表示这种方案失败,换一种方案再继续搜索,这样就会少递归很多次。
⑤剪枝优化2:如果前一个人和这个人的嘴一样大,那么就可以优化判断前面的人是否可以被满足,减少for循环次数,由于这个人在第i个蛋糕之前的蛋糕都已经无法满足了(所以才会使用第i个蛋糕来满足),因为前一个人和这个人嘴一样大,所以前i个蛋糕也无法满足这个人了,因此,下一次循环可以特意从当前的i开始循环,而same_start也就是这样起到标记效果的。
▎Code speaks louder than words!
废话不多说了,详细的地方都已经写好了注释,直接上代码吧!
1 #include<iostream> 2 #include<algorithm> 3 #define bug cout<<"no error!"; 4 using namespace std; 5 int mouth[10000],cake[10000],c[10000],pre[10000],waste,all,n,m,l,r,mid,ans,maxn;//变量的意思(依次) 6 //嘴的大小、蛋糕的大小、蛋糕大小副本、前缀和、浪费值、蛋糕总体积 、蛋糕个数、嘴的个数、二分左边界、右边界 7 //二分的中点、答案、最大的蛋糕的体积 8 int dfs(int num,int same_start)//num表示剩下的要满足的人数,同时也巧妙的表示了人嘴的编号 9 //same_start未剪枝时都可以当做1,而在进行剪枝时的用处详见上文 10 { 11 if(num==0) return 1;//能够分配完所有的人,那么返回1 12 if(all-waste<pre[mid]) return 0;//剪枝优化1,详见上文 13 for(int i=same_start;i<=n;i++) 14 { 15 if(c[i]>=mouth[num]) 16 { 17 c[i]-=mouth[num];//如果能满足这个人,那么就让他吃掉,进行试探 18 if(c[i]<mouth[1]) waste+=c[i];//如果连口最小的人都满足不了, 19 //那么只能浪费,于是增加浪费值,便于上面的剪枝 20 if(mouth[num]==mouth[num-1])//剪枝优化2,详见上文 21 { 22 if(dfs(num-1,i)) return 1; 23 } 24 else if(dfs(num-1,1)) return 1; 25 if(c[i]<mouth[1]) waste-=c[i];//回溯 26 c[i]+=mouth[num];//回溯 27 } 28 } 29 return 0;//如果是可以满足的,那么上面会返回的,否则就是不可以满足,返回0 30 } 31 int main() 32 { 33 cin>>n; 34 for(int i=1;i<=n;i++) 35 { 36 cin>>cake[i]; 37 all+=cake[i];//记录蛋糕总量,用于剪枝 38 if(cake[i]>maxn) maxn=cake[i];//记录最大的蛋糕大小,后面有用 39 } 40 cin>>m; 41 for(int i=1;i<=m;i++) 42 cin>>mouth[i]; 43 sort(mouth+1,mouth+m+1);//贪心:将每个人按嘴的大小排序 44 while(maxn<mouth[m]) m--;//从嘴最大的人开始,如果嘴比最大的蛋糕还大,那么一定无法满足 45 //因为无法将两块蛋糕拼起来给人 46 for(int i=1;i<=m;i++) 47 pre[i]=pre[i-1]+mouth[i];//记录前缀和,用于剪枝 48 l=0;r=m;//规定好二分查找左右边界 49 while(l<=r) 50 { 51 waste=0;//浪费值初始为0 52 mid=(l+r)/2; 53 for(int i=1;i<=n;i++) c[i]=cake[i];//如果在搜索中用cake数组的话,可能在没有回溯前就返回了, 54 //那样cake值会变,影响下一轮搜索,所以赋值到c数组中,使用c数组代替,就像是常说的副本一样 55 if(dfs(mid,1)) 56 { 57 ans=mid;//如果这个猜测能完成,那么就要记录下答案,不停覆盖,直到最后找到 58 l=mid+1; 59 } 60 else r=mid-1;//注意:这里千万不要写成r=mid, 61 //因为当l=r时,mid=l=r,如果r=mid,那么就会陷入死循环,可以自己模拟一下,l会永远等于r 62 //这种情况不可能r<l,所以会一直循环 63 //或者这里写成r=mid,但是while的小括号里必须换一个判定条件:l<r也是可以的 64 } 65 cout<<ans; 66 return 0; 67 }








