Kattis-A Towering Problem

题目所述基本内容

You’ve been put in charge of an art exhibit from the famous minimalist sculptor J (even his name is minimalist!). J’s work involves the careful layout of vertically dispositioned orthogonal parallelpipeds in a set of tapering obelisks — in other words, he puts smaller boxes on top of larger boxes. His most recent triumph is called “2 by 3’s Decreasing,” in which he has various sets of six boxes arranged in two stacks of three boxes each. One such set is shown below:

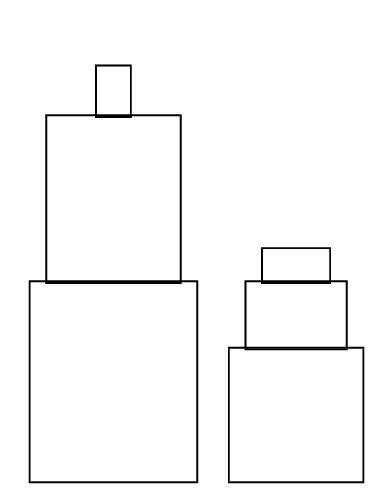
J has sent you the art exhibit and it is your job to set up each of the six-box sets at various locations throughout the museum. But when the sculptures arrived at the museum, uncultured barbarians (i.e., delivery men) simply dropped each set of six boxes on the floor, not realizing the aesthetic appeal of their original layout. You need to reconstruct each set of two towers, but you have no idea which box goes on top of the other! All you know is the following: for each set of six, you have the heights of the two towers, and you know that in any tower the largest height box is always on the bottom and the smallest height box is on the top. Armed with this information, you hope to be able to figure out which boxes go together before tomorrow night’s grand opening gala. 

输入输出样例

Input

The input consists of eight positive integers. The first six represent the heights of the six boxes. These values will be given in no particular order and no two will be equal.

The last two values (which will never be the same) are the heights of the two towers.

All box heights will be ≤100 and the sum of the box heights will equal the sum of the tower heights.

Output

Output the heights of the three boxes in the first tower (i.e., the tower specified by the first tower height in the input), then the heights of the three boxes in the second tower. Each set of boxes should be output in order of decreasing height. Each test case will have a unique answer.

12 8 2 4 10 3 25 14

12 10 3 8 4 2

12 17 36 37 51 63 92 124

63 17 12 51 37 36

代码

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
#define Num 8bool GreaterSort(int a, int b)
{return (a > b);
}int main() {vector<int>arr(8);vector<int>result;int time = 0;int temp = 0;for (int i = 0; i < Num; i++) {cin >> temp;arr[i] = temp;}sort(arr.begin(), arr.begin() + Num-2, GreaterSort);for (int i = 0; i < Num-2; i++) {for (int j = i + 1; j < Num-2; j++) {for (int k = j + 1; k < Num-2; k++) {if (arr[i] + arr[j] + arr[k] == arr[6]) {result.push_back(arr[i]);result.push_back(arr[j]);result.push_back(arr[k]);}}}}for (int i = 0; i < Num - 2; i++) {time = 0;for (int j = 0; j < 3; j++) {if (arr[i] != result[j]) {time++;if (time == 3) {result.push_back(arr[i]);}}}}for (int i = 0; i < Num-2; i++) {cout << result[i] << " ";}return 0;
}

结束语

好兄弟好兄弟，留下你的关注和点赞，666走一波！！！！！