Josephus算法——C语言

据说著名犹太历史学家 Josephus有过以下的故事：在罗马人占领乔塔帕特后，39 个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式：41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始，越过k-2个人（因为第一个人已经被越过），并杀掉第k个人。接着，再越过k-1个人，并杀掉第k个人。这个过程沿着圆圈一直进行，直到最终只剩下一个人留下，这个人就可以继续活着。问题是一开始要站在什么地方才能避免自杀？Josephus要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。
17世纪的法国数学家加斯帕在《数目的游戏问题》中讲了这样一个故事：15个教徒和15个非教徒在深海上遇险，必须将一半的人投入海中，其余的人才能幸免于难，于是想了一个办法：30个人围成一圆圈，从第一个人开始依次报数，每数到第九个人就将他扔入大海，如此循环进行直到仅余15个人为止。问怎样排法，才能使每次投入大海的都是非教徒。
——摘自约瑟夫问题_百度百科

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
typedef struct ren{//队伍内部形式 int data;struct ren *next;
}link,*linklist;typedef struct h{//头指针 linklist next;
}head;//#define int A 40
void add(head *L,int n)//添加初始化队伍人数n为最大人数L为队伍名称 
{if(n>0){linklist q=(linklist)malloc(sizeof(link));q->next=L->next;L->next=q;q->data=n;add(L,n-1);}return;
}//添加队伍初始人数void chuan(head *L){//将链表连成串 linklist p,pre;;p=L->next;while(p){pre=p;p=p->next;}pre->next=L->next;}void kill(head *L,int n,int last,int fk){//开始杀人 n为总人数 last为所剩人数 fk为间隔人数 linklist p,pre;//每隔N人开杀 p=L->next;pre=p;//留存点 int k=0;for(int i=0;i<n&&(n-i)>=last&&(n-i)>=fk;i++){k=1;//k为什么等于1呢，是因为。。。其实你们画个图就明白了，三跟一之间只有两个元素嘛！ while(k<fk)//找到第fk个人 {k++;pre=p;p=p->next;}if(p==pre){//全杀完了 L->next=NULL;printf("全杀完了！\n");return;	}else{//杀掉那个伙计 pre->next=pre->next->next;if(L->next==p)//如果删除的是头结点，那么赶紧转身扯呼！ {L->next=p->next;}free(p);p=pre->next;}}
}
void puut(head *L){//输出linklist p,q;p=q=L->next;if(p)printf("%d\t",p->data);p=q->next;while(p!=q){printf("%d\t",p->data);p=p->next;}
}int main(){head * L;int A=41;L->next=NULL;add(L,A);//创建链表L chuan(L);puut(L);printf("\n");kill(L,A,0,3); puut(L);
return 0;
}/*两个问题 
1、头指针指示链表会导致一个问题，就是删除元素期间，容易将头指针指示的元素一并删除，极易导致链表丢失的情况
2、如何判定删除的只剩 (诶！我想出来了！哈哈哈第二个不是问题了，，应该吧，我测试一下先)更新二：
现在问题大部分都解决了，只剩下让循环链表停止循环输出的问题
话说，我这释放循环指针之后，头链表还能将元素输出出来挺神奇的啊！
我懂了！头链表指向的是第一个元素，将链表中的元素释放之后
我并未释放头指针指向的空间，好吧经过测试发现，并非我所猜测的出现两个问题
虽然跟结果类似，但严谨的我还是要找出问题的关键所在第一、虽然答案输出，但为何循环输出
问题关键在两点：1、输入函数建设问题；
2、输出函数循环问题总归在函数的处理方面还算没问题吧！
但输入输出问题关键很大！ 哎！问题解决了
这个道理很简单，
既然无法管删除头结点会不会影响大局，那就不让它删到头结点嘛！！！ 
*/

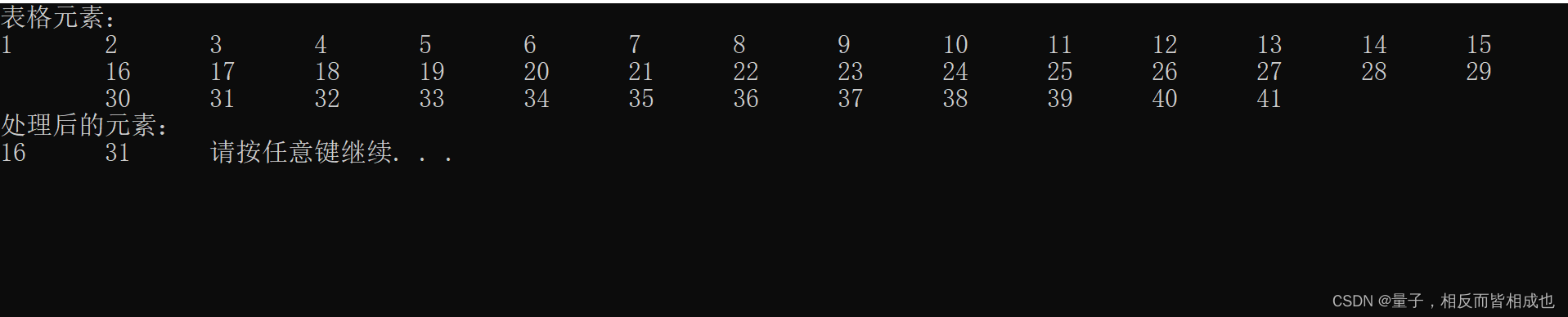
最近在准备考研，一直执着于手写算法，突然上机一次，发现很多日常没注意的问题都暴露了出来，恩！以后要多多上机测试自己的代码能力