本文主要是介绍Processing+代码本色 chap3 振荡,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
弹力
介绍
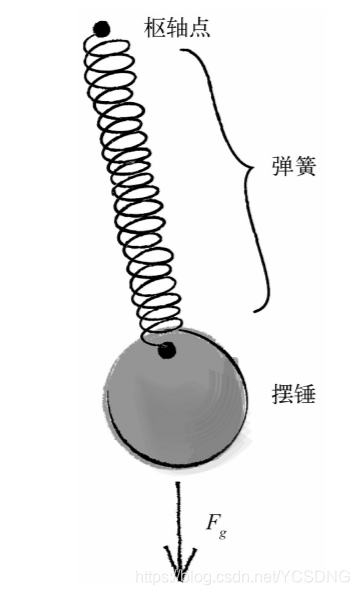
弹簧的弹力可以根据胡克定律计算得到,胡克定律以英国物理学家罗伯特·胡克命名,他在1660年发明了这个公式。胡克最初是用拉丁文描述这个公式的——“Ut tensio,sic vis”, 这句话的意思是“力如伸长(那样变化)”。我们可以这么理解它:弹簧的弹力与弹簧的伸长量成正比。
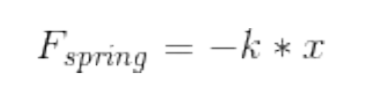
先用胡克定律计算弹力的大小。我们需要知道k和x的值:k很简单,它只是一个常量,我们可以随意选择一个数。
float k = 0.1;
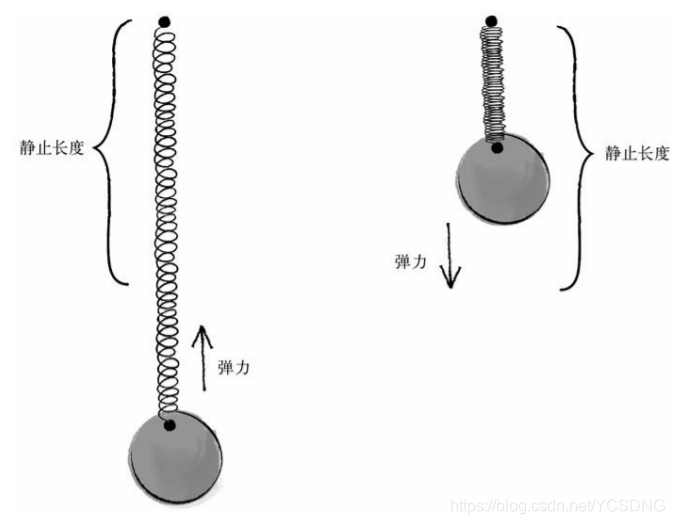
x可能会更复杂,我们需要知道“当前长度和静止长度的差”。可以用restLength表示静止长度,
PVector dir = PVector.sub(bob,anchor); 由枢轴点指向摆锤的向量,它告诉我们弹簧的当前长度
float currentLength = dir.mag();
float x = restLength - currentLength;
方向计算
float k = 0.1; 按照胡克定律计算得到的弹力
PVector force = PVector.sub(bob,anchor);
float currentLength = dir.mag();
float x = restLength - currentLength;
force.normalize(); 弹力的方向(单位向量)
force.mult(-1 k x); 把方向和大小放在一起!
下面两个类不做过多介绍,可以参考书本第三章的介绍
Spring类的实现
class Spring { PVector anchor;// 静止长度和弹簧常数float len;float k = 0.2;Bob a;Bob b;// Spring(Bob a_, Bob b_, int l) {a = a_;b = b_;len = l;} // Calculate spring forcevoid update() {// Vector pointing from anchor to bob positionPVector force = PVector.sub(a.position, b.position);// What is distancefloat d = force.mag();// Stretch is difference between current distance and rest lengthfloat stretch = d - len;// Calculate force according to Hooke's Lawforce.normalize();force.mult(-1 * k * stretch);a.applyForce(force);force.mult(-1);b.applyForce(force);}void display() {strokeWeight(2);stroke(0);line(a.position.x, a.position.y, b.position.x, b.position.y);}
}
控制小球的类(Bob类)
class Bob { PVector position;PVector velocity;PVector acceleration;float mass = 12;// Arbitrary damping to simulate friction / drag float damping = 0.95;// For mouse interactionPVector dragOffset;boolean dragging = false;// ConstructorBob(float x, float y) {position = new PVector(x,y);velocity = new PVector();acceleration = new PVector();dragOffset = new PVector();} // Standard Euler integrationvoid update() { velocity.add(acceleration);velocity.mult(damping);position.add(velocity);acceleration.mult(0);}// Newton's law: F = M * Avoid applyForce(PVector force) {PVector f = force.get();f.div(mass);acceleration.add(f);}// Draw the bobvoid display() { stroke(0);strokeWeight(2);fill(175);if (dragging) {fill(50);}ellipse(position.x,position.y,mass*2,mass*2);} // The methods below are for mouse interaction// This checks to see if we clicked on the movervoid clicked(int mx, int my) {float d = dist(mx,my,position.x,position.y);if (d < mass) {dragging = true;dragOffset.x = position.x-mx;dragOffset.y = position.y-my;}}void stopDragging() {dragging = false;}void drag(int mx, int my) {if (dragging) {position.x = mx + dragOffset.x;position.y = my + dragOffset.y;}}
}
网格设计
根据上面两个类对网进行实现
int Bobnum = 10;
Bob[][] b = new Bob[Bobnum][Bobnum];
Spring[] s = new Spring[2*Bobnum*(Bobnum-1)];
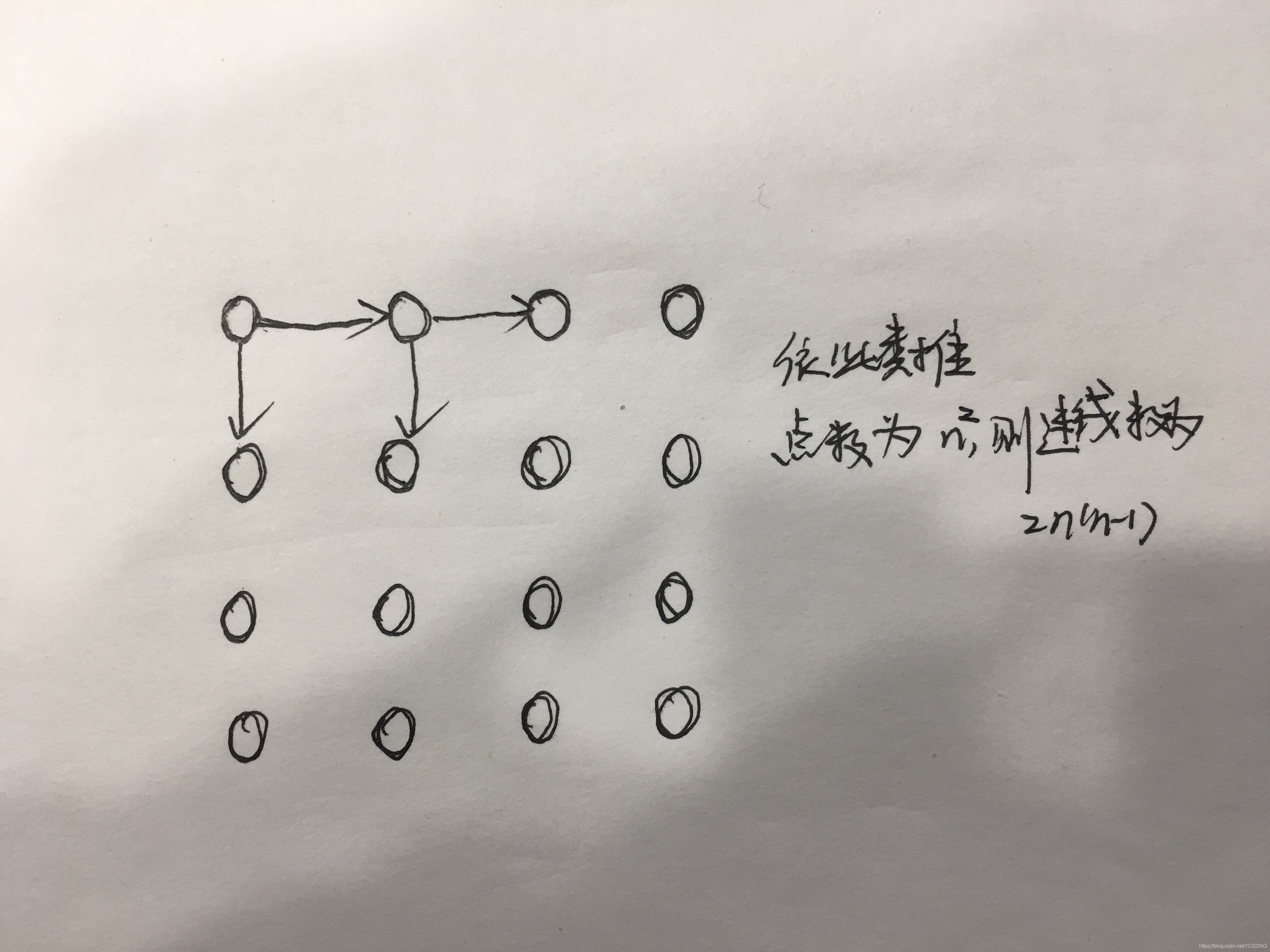
Bobnum:网的长度(即每一行的点的个数,宽度和长度相等)
b:存储网的点的数组
s:存储点之间连线的数组
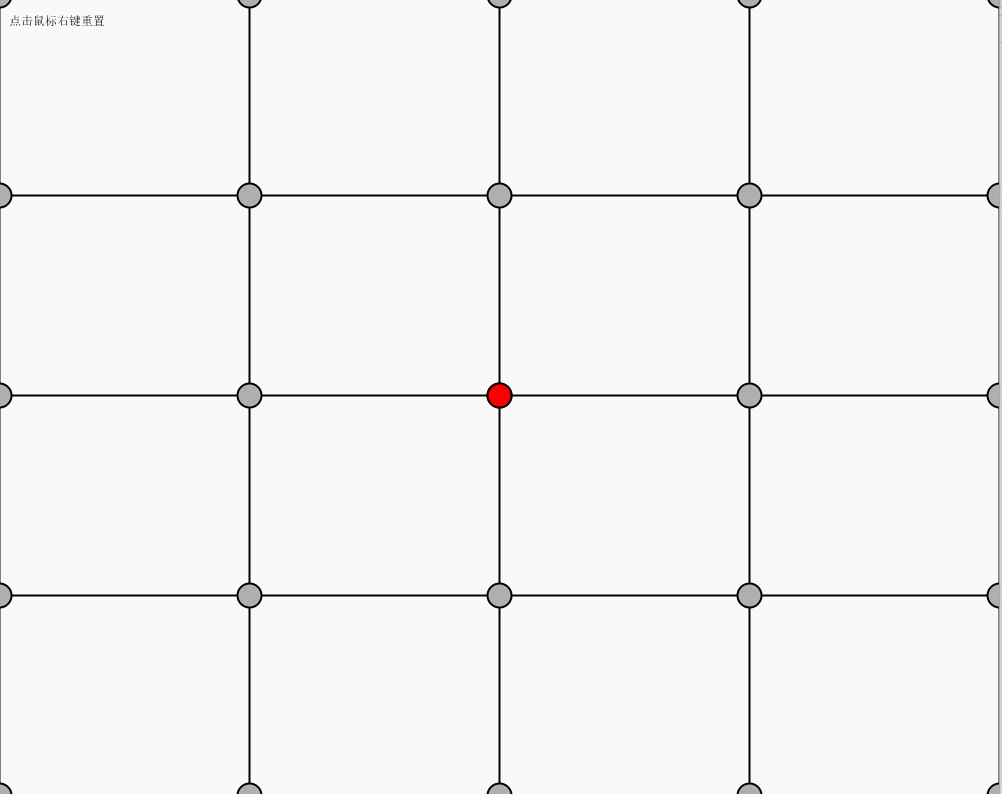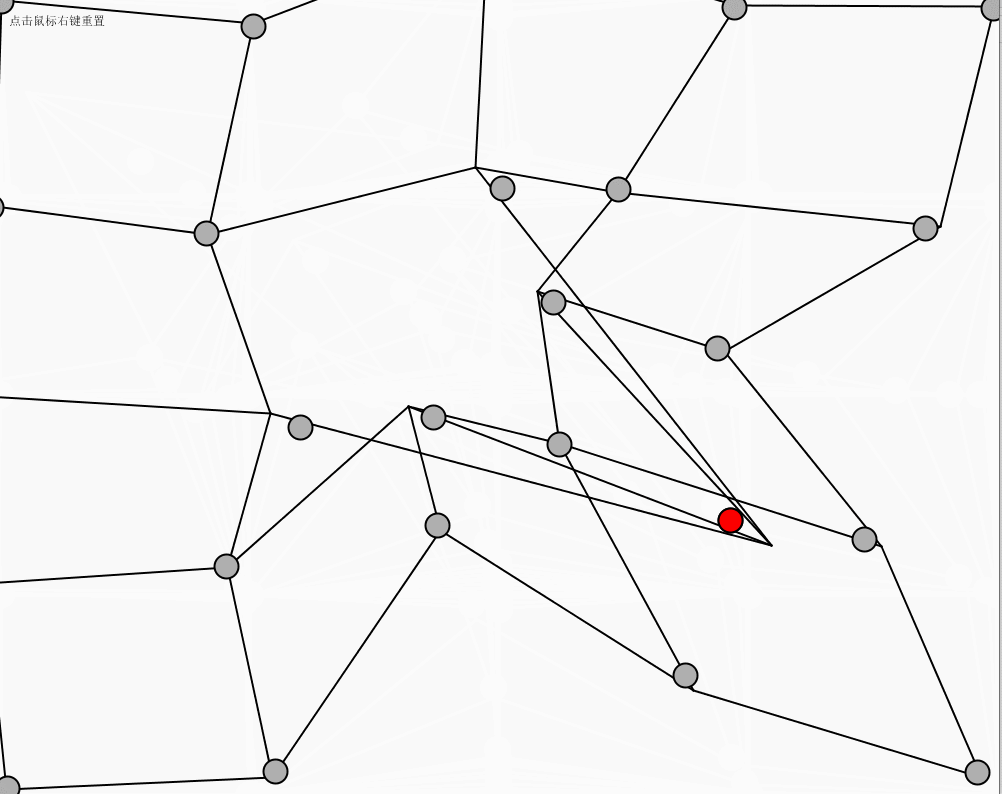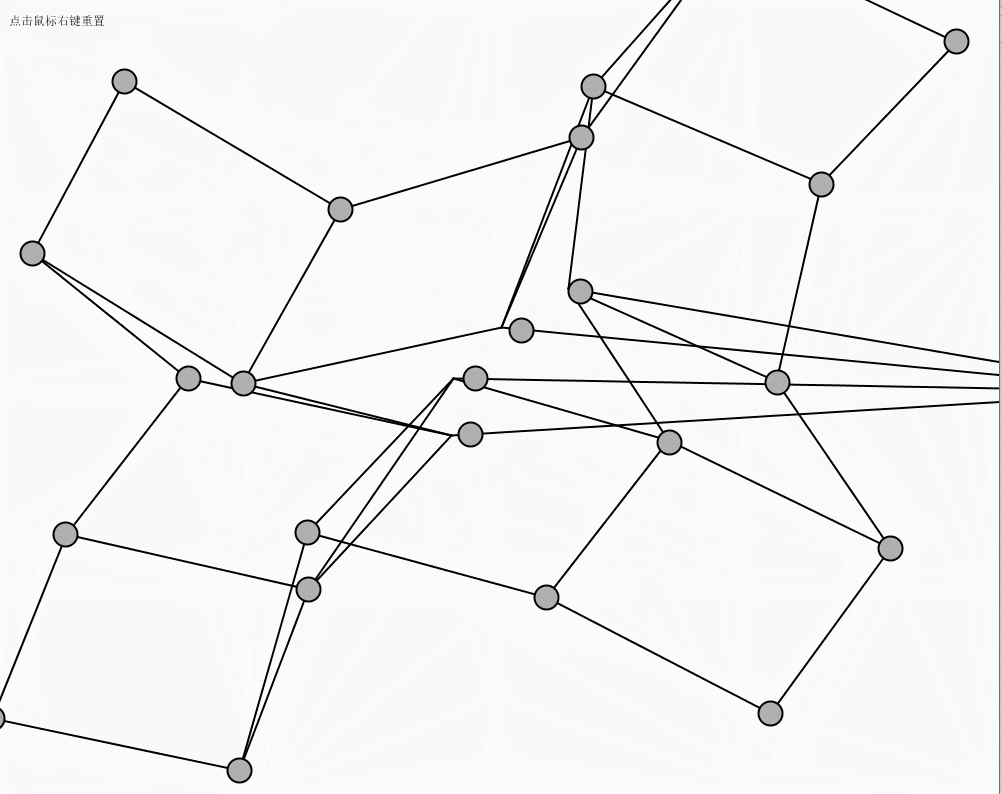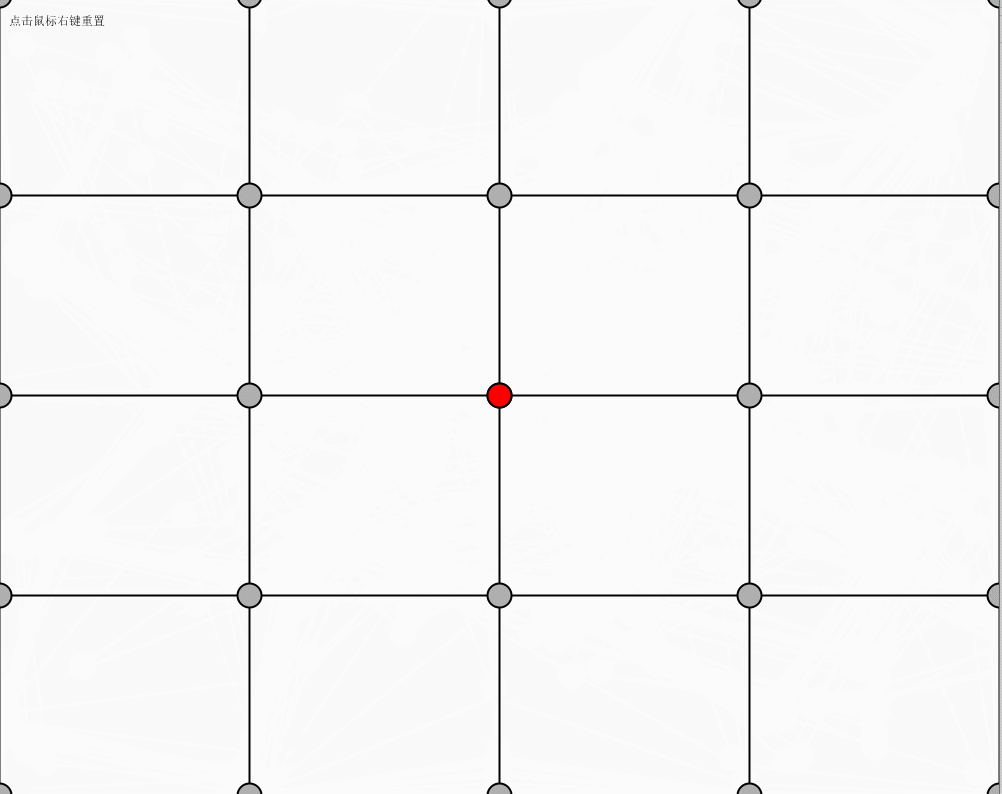
对数组进行初始化,连线方式参考上图
void setup() {size(1000, 800);// 在起始位置创建对象//请注意,Spring构造函数中的第三个参数是"rest length"int Springnum = 0;for(int i=0;i<Bobnum;i++)for(int j=0;j<Bobnum;j++)b[i][j] = new Bob(width*j/(Bobnum-1),height*i/((Bobnum-1)));for(int i=0;i<Bobnum;i++)for(int j=0;j<Bobnum;j++){if(j<Bobnum-1&&i<Bobnum-1){s[Springnum] = new Spring(b[i][j],b[i][j+1],int(width/(Bobnum-1)));s[Springnum+1] = new Spring(b[i][j],b[i+1][j],int(height/((Bobnum-1))));Springnum +=2;}else{if(j==Bobnum-1 &&i<Bobnum-1){s[Springnum] = new Spring(b[i][j],b[i+1][j],int(height/((Bobnum-1))));Springnum+=1;}else if(j<Bobnum-1&&i==Bobnum-1){s[Springnum] = new Spring(b[i][j],b[i][j+1],int(width/(Bobnum-1)));Springnum +=1;}else{}}}
}
在draw()函数中进行实现
void draw() {background(255); for(int a=0;a<2*Bobnum*(Bobnum-1);a++)s[a].update();for(int a=0;a<2*Bobnum*(Bobnum-1);a++)s[a].display();for(int i=0;i<Bobnum;i++)for(int j=0;j<Bobnum;j++){b[i][j].update();b[i][j].display();}b[int(Bobnum/2)][int(Bobnum/2)].drag(mouseX, mouseY);fill(255,0,0);ellipse(b[int(Bobnum/2)][int(Bobnum/2)].position.x,b[int(Bobnum/2)][int(Bobnum/2)].position.y,b[int(Bobnum/2)][int(Bobnum/2)].mass*2,b[int(Bobnum/2)][int(Bobnum/2)].mass*2);fill(0);text("点击鼠标右键重置", 10, 30);
}
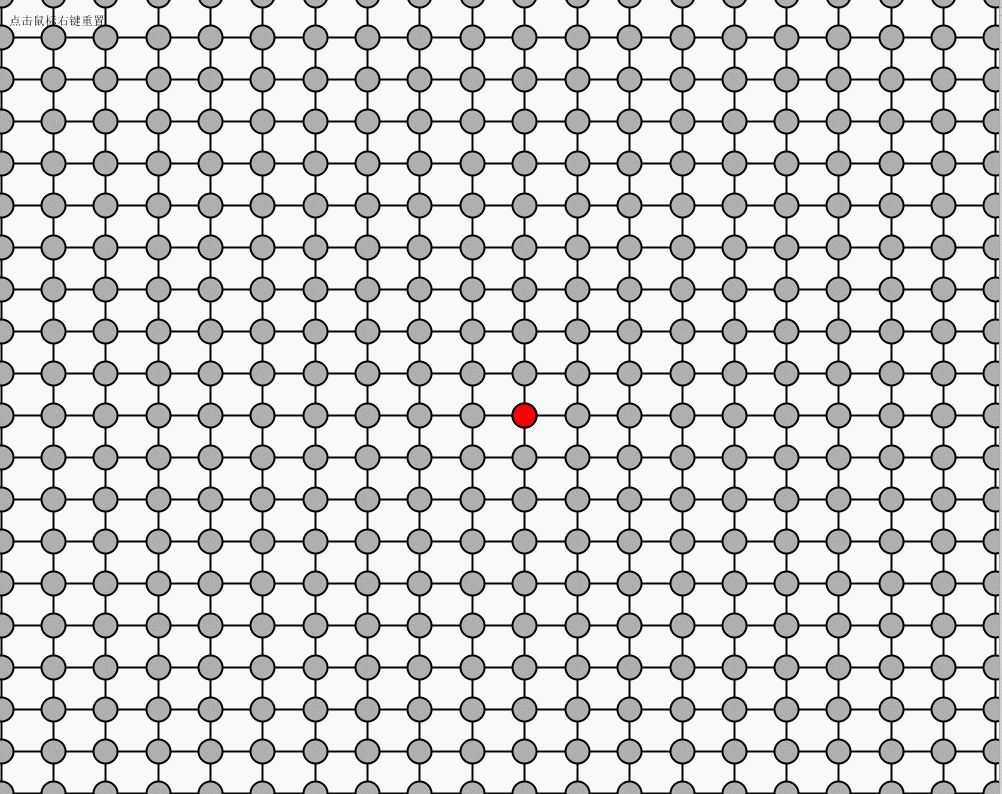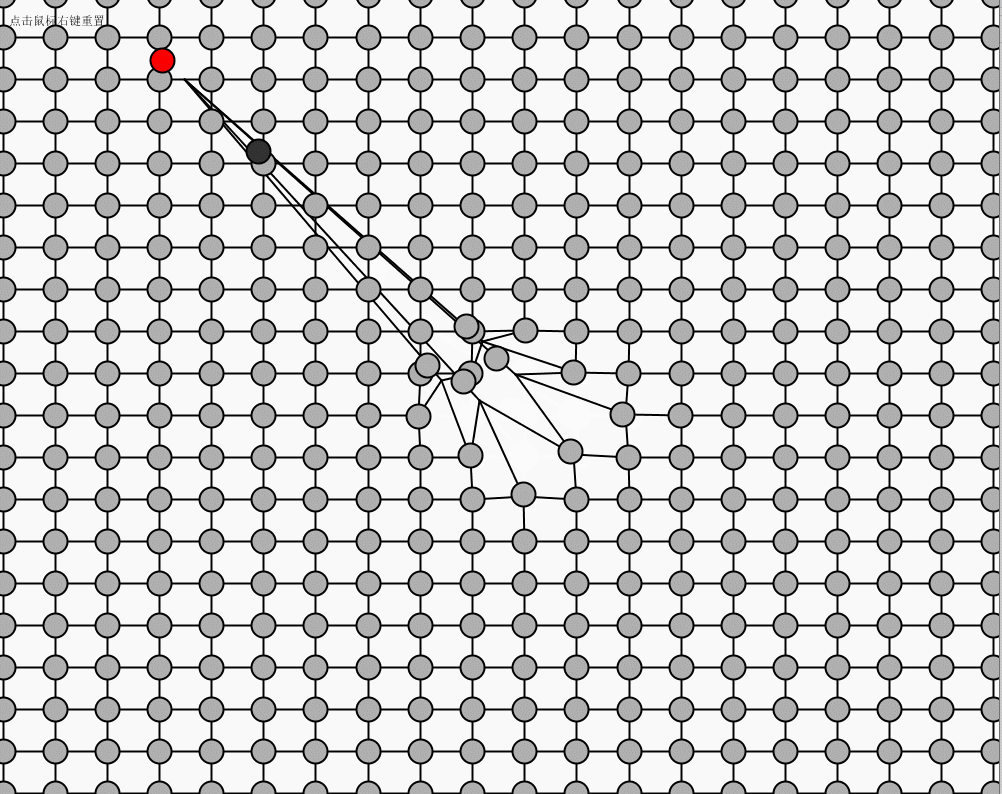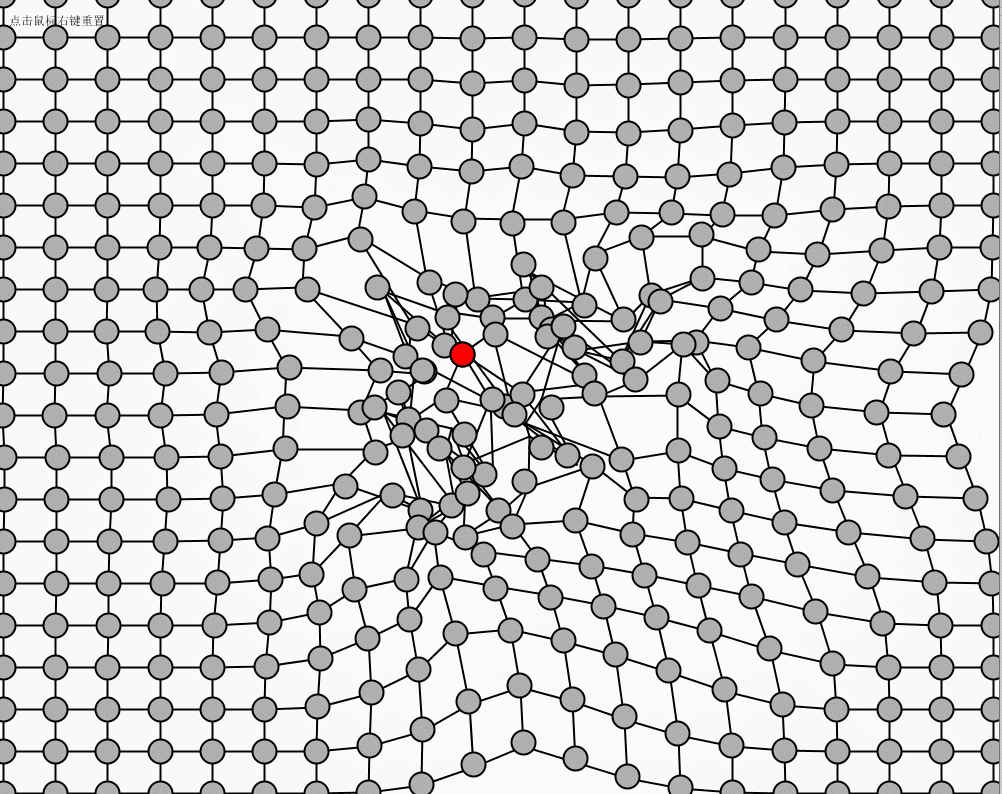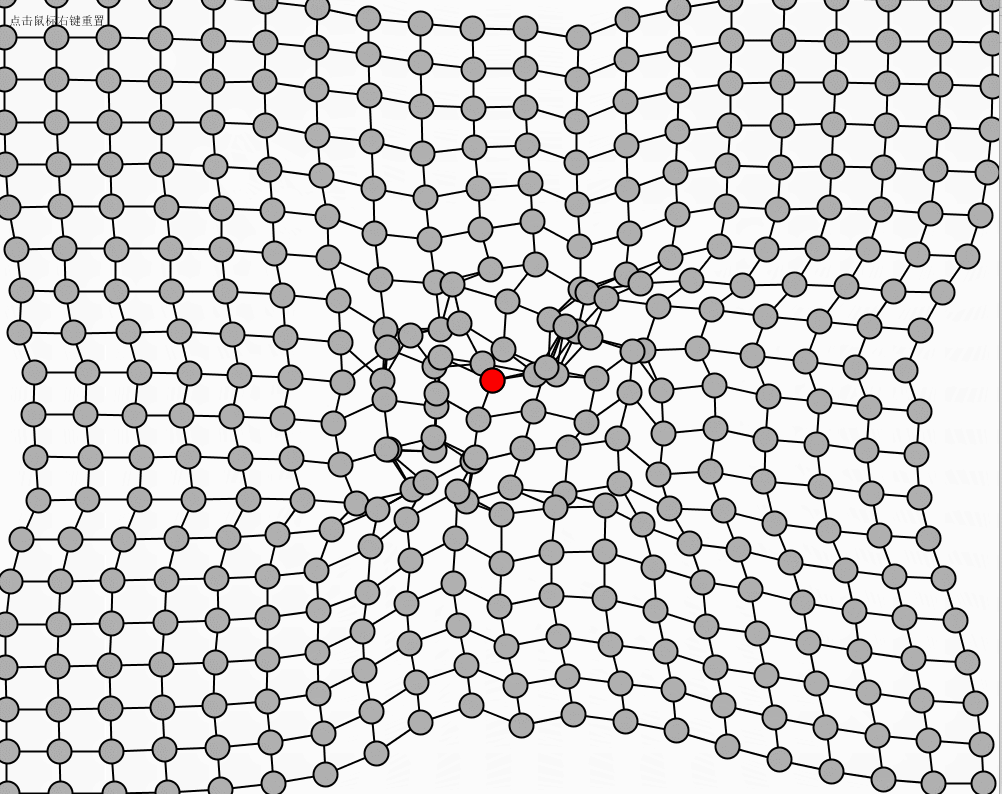
点击鼠标右键进行网的初始位置重现,鼠标左键点击红色的球可以进行拖动。
void mousePressed() {if (mouseButton == RIGHT){setup();}b[int(Bobnum/2)][int(Bobnum/2)].clicked(mouseX, mouseY);
}void mouseReleased() {b[int(Bobnum/2)][int(Bobnum/2)].stopDragging();
}
运行效果
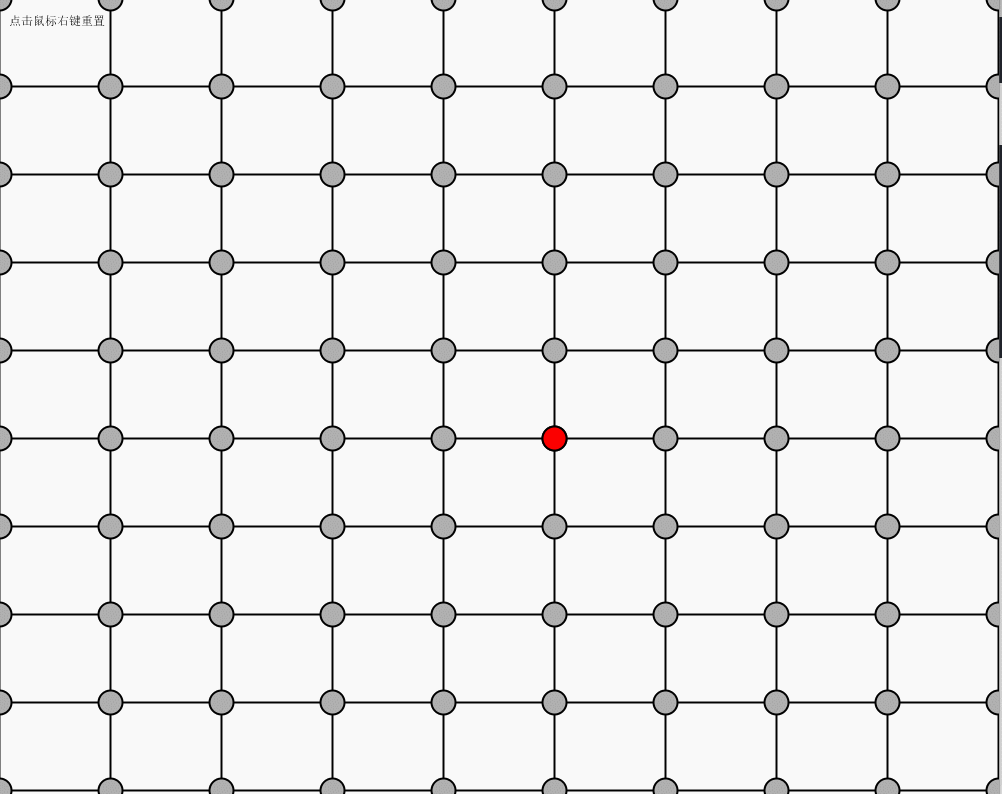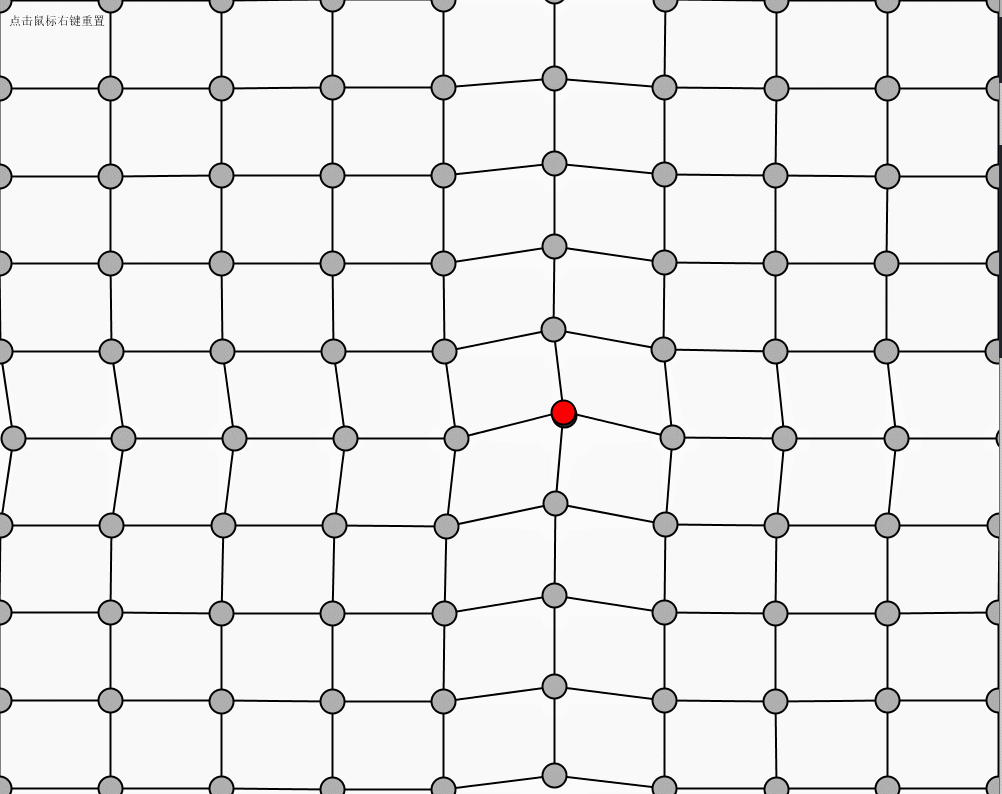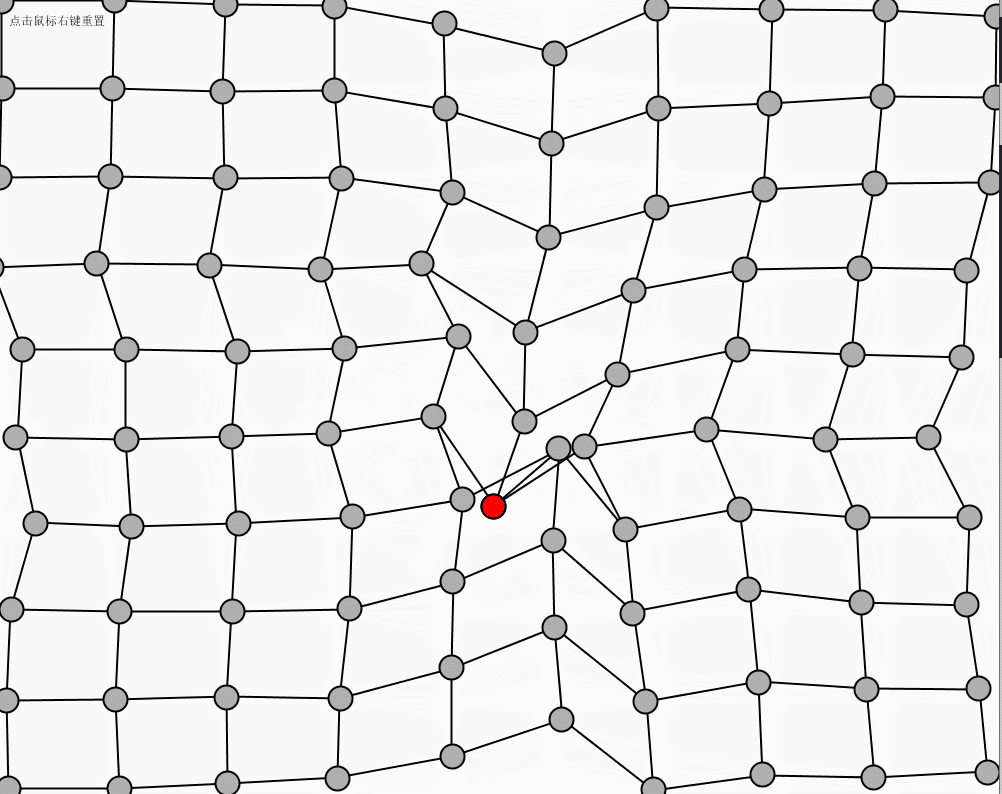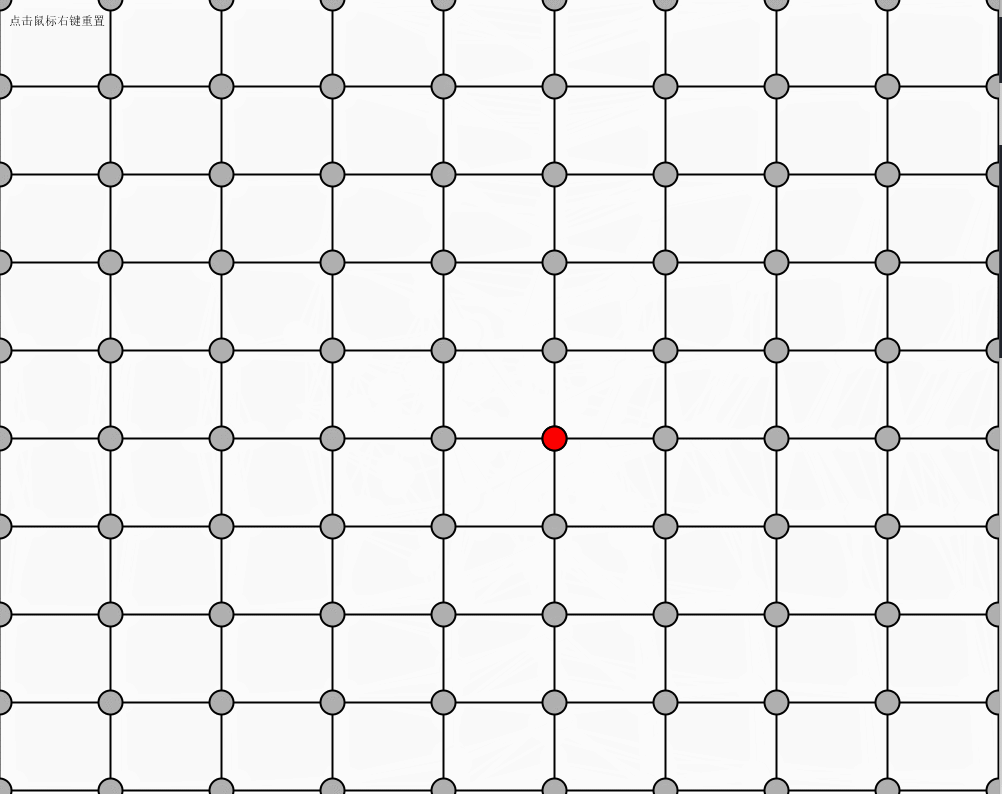

这篇关于Processing+代码本色 chap3 振荡的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!