光学显微镜算法(OMA)(含MATLAB代码)

先做一个声明：文章是由我的个人公众号中的推送直接复制粘贴而来，因此对智能优化算法感兴趣的朋友，可关注我的个人公众号：启发式算法讨论。我会不定期在公众号里分享不同的智能优化算法，经典的，或者是近几年提出的新型智能优化算法，并附MATLAB代码。

“今天分享的算法是2023年9月3日才Online的，到今天还没有一个周，可以说是最新的一个智能优化算法之一，发表在KBS上~

我比较欣赏这个算法的灵感来源，觉得它的数学建模过程比较有趣。”

光学显微镜算法(Optical Microscope Algorithm, OMA)从光学显微镜对目标物体的放大能力中获得灵感，使用肉眼进行初始观察，并通过物镜和目镜模拟放大过程。通过两个实验验证了OMA的性能，该算法具有用户友好且不需要初始化参数的特点：(1)在50个Benchmark函数上，将OMA与九种启发式算法进行比较，结果表明OMA性能更优、计算时间更短；(2)将OMA应用于解决工程问题，包括多项目调度中的结构优化和多资源均衡。OMA不仅显示出优越性，而且使用目标函数评估次数最少。该算法具有鲁棒性好、易于实现、控制参数少等特点，可用于求解多种数值优化问题。它的原始参考文献如下：

“Cheng MY, Sholeh MN. Optical microscope algorithm: A new metaheuristic inspired by microscope magnification for solving engineering optimization problems[J]. Knowledge-Based Systems, 2023: 110939.”

01
灵感来源

我比较喜欢这个算法的模型灵感来源。下面，我就说一下我的理解：我们在使用显微镜观察物体时，都需要调试物镜和目镜，找到一个最优的观察效果。那么，这个最优的观察效果就对应于算法所要寻找的最优解，而调试物镜、目镜的过程，就对应于种群的迭代，即不断调试物镜和目镜相当于种群的不断进化。将物体放到显微镜载物台就对应于算法的种群初始化。这个抽象的过程由图1所示，算法的循环迭代即是不断调整物镜和目镜，以寻找最优的观察角度。

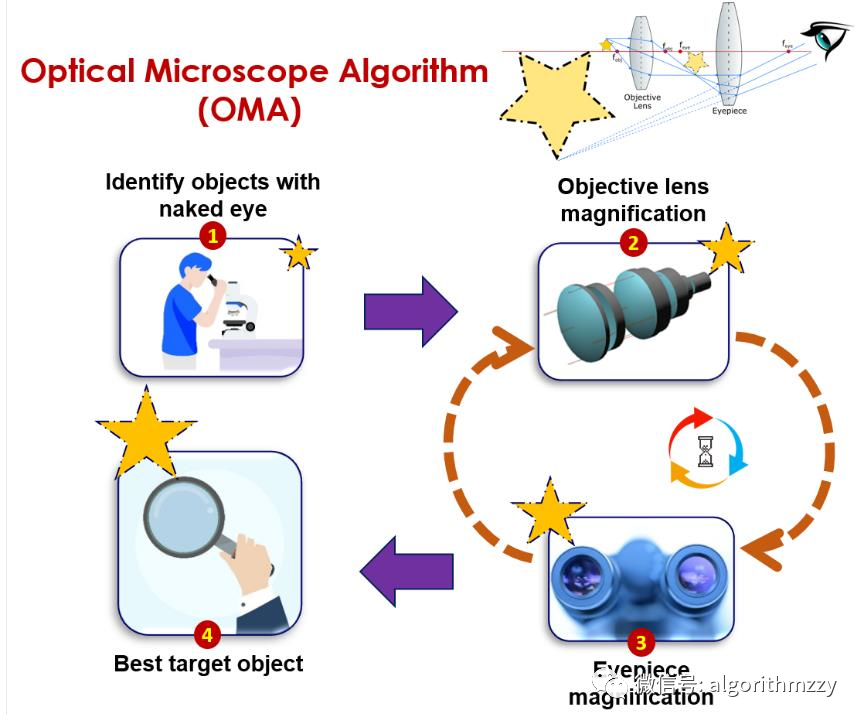
图1 OMA的算法框架

02
算法设计

与往期推送一样，目前我还不会在公众号里编辑数学公式。因此，这部分内容在Word文档里先写好，然后做成图片，最后导入。

（讲真说来，OMA的设计挺简单的，就两个位置更新公式，一个对应于物镜放大，一个对应于目镜放大。）

03
计算流程

OMA的计算流程图如图2所示（注意：图2截自GOA的原文，因此图中的符号含义需要对照原文看）：

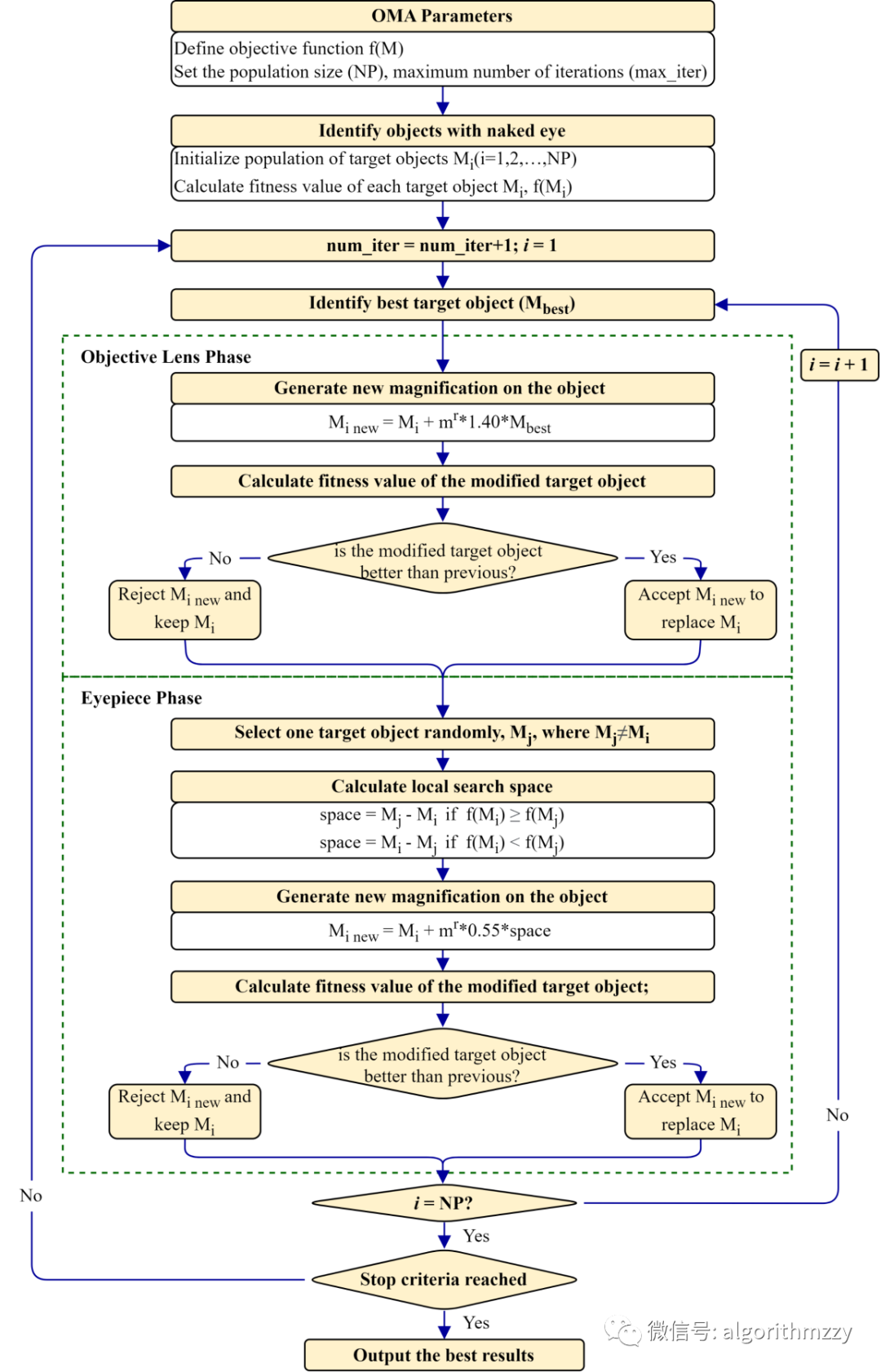
图2 OMA的计算流程图

04
实验仿真

这里对OMA的性能进行简单的测试。首先将OMA用于函数寻优，算法的MATLAB程序是严格按照它的原始参考文献进行编码的。此外，种群规模取N等于50，Benchmark函数分别采用了CEC2005测试集、CEC2013测试集、CEC2014测试集、CEC2017测试集、CEC2020优化函数测试集和CEC2022优化函数测试集。这里对仿真结果进行简要展示，不再进一步分析。

首先，检验一下OMA对全局勘探和局部开发的平衡能力。不知道我在说啥的，看一下之前的这一期推送：
种群的勘探(Exploration)与开发(Exploitation)(含MATLAB代码)
如图3所示，是OMA在CEC2005测试函数f7上的勘探和开发占比曲线。

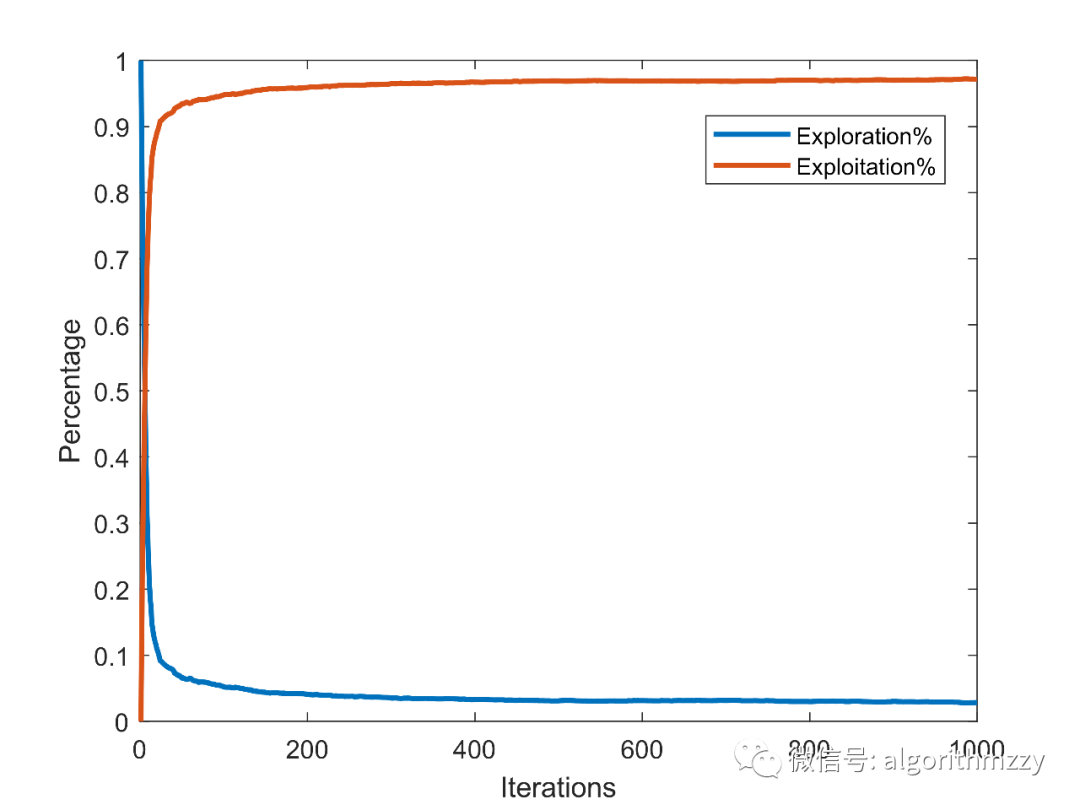
图2 OMA在CEC2005 f7上的勘探和开发百分占比变化曲线

其次，以CEC2005的单峰函数Schwefel's 2.22 (f2)为例，展示OMA在30维环境下的收敛效果，如图4所示。

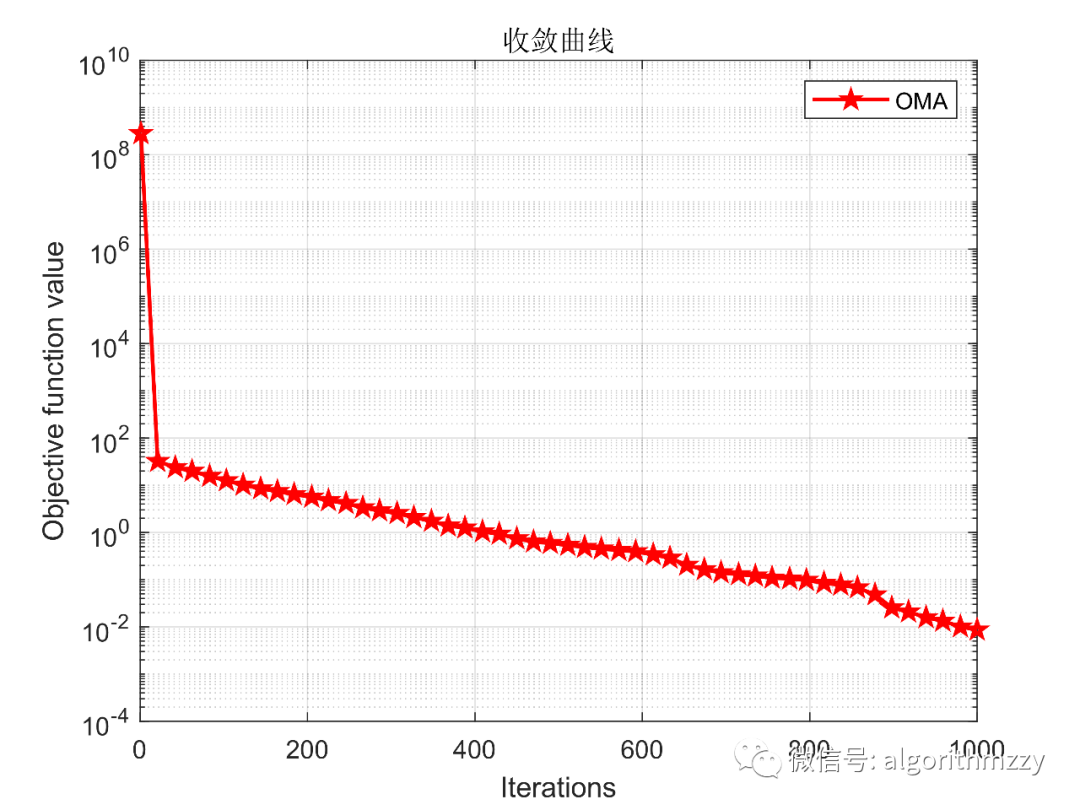
图4 OMA在CEC2005 f2测试函数上的收敛曲线

再次，以CEC2013测试集中的单峰函数F1为例，展示OMA在30维环境下的收敛效果，如图5所示。(注意是画的误差曲线)

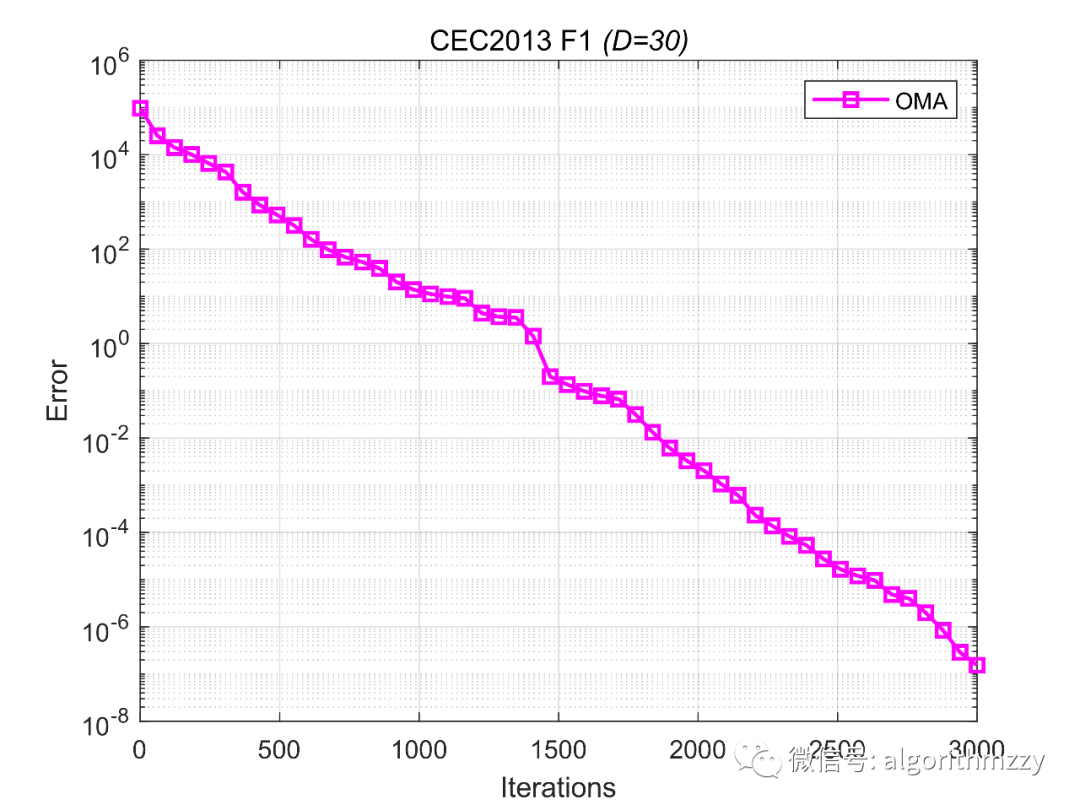
图5 OMA在CEC2013 F1上的误差收敛曲线

接着，以CEC2014测试集中的多模态函数F14为例，展示OMA在30维环境下的收敛效果，如图6所示。(注意是画的误差曲线)

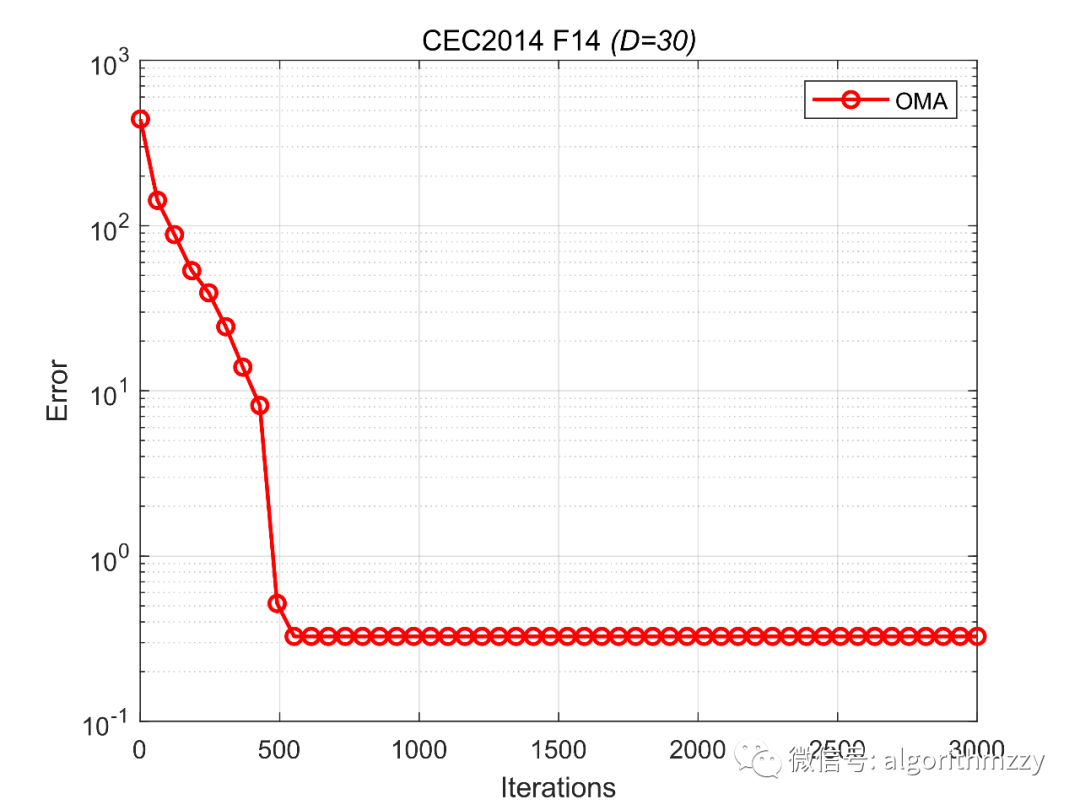
图6 OMA在CEC2014 F14上的误差收敛曲线

再然后，以CEC2017测试集中的多模态函数F4为例，展示OMA在30维环境下的收敛效果，如图7所示。(注意是画的误差曲线)

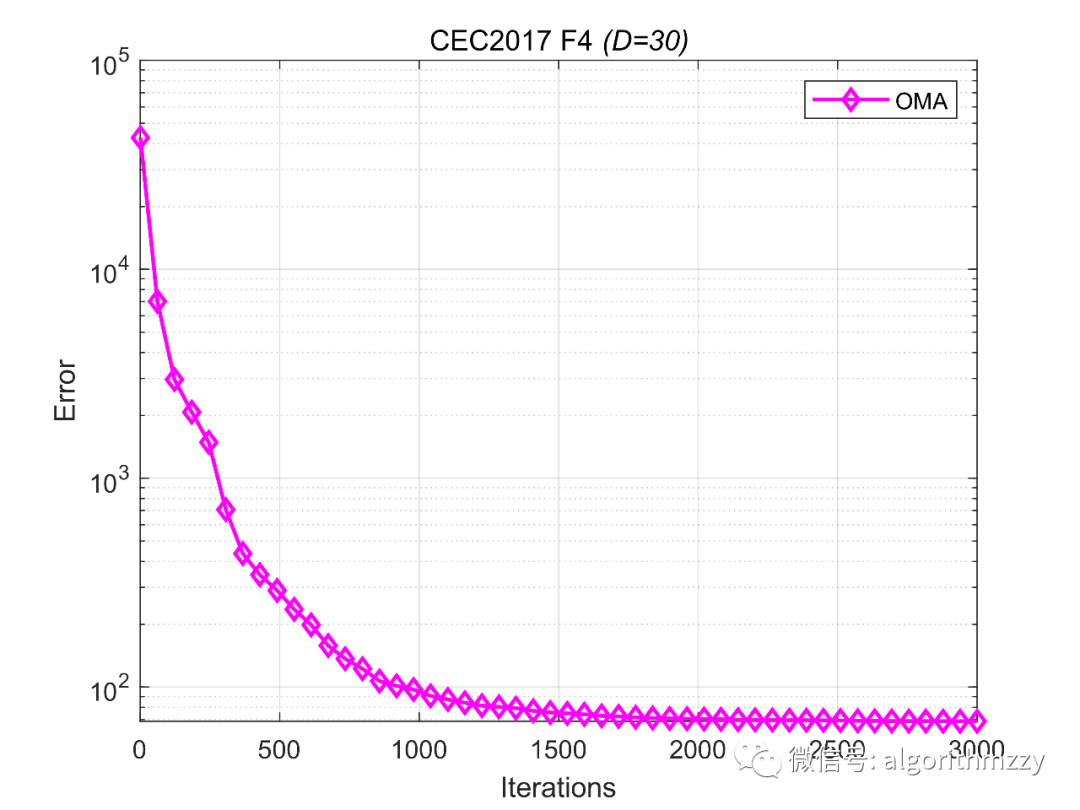
图7 OMA在CEC2017 F4上的误差收敛曲线

在此之后，以CEC2020优化函数测试集中的单峰函数F2为例，展示OMA在10维环境下的收敛效果，如图8所示。(注意是画的误差曲线)

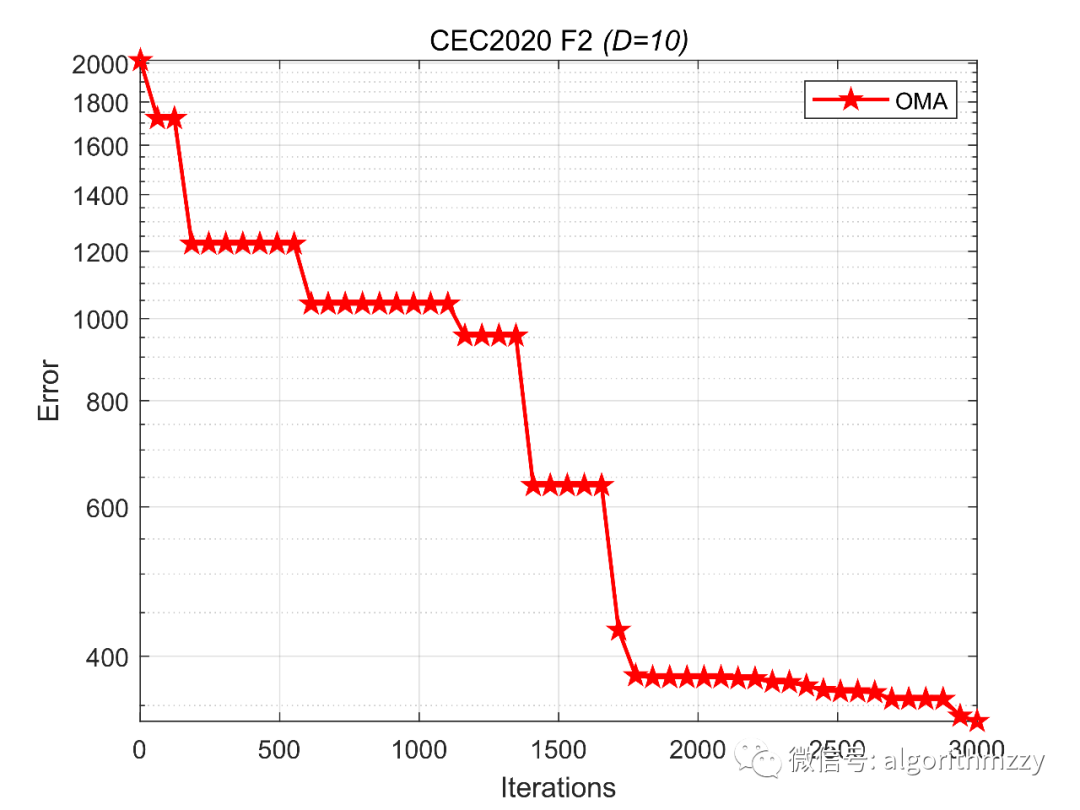
图8 OMA在CEC2020优化函数F2上的误差收敛曲线

最后，以CEC2022优化函数测试集中的单峰函数F1为例，展示OMA在10维环境下的收敛效果，如图9所示。(注意是画的误差曲线)

图9 OMA在CEC2022优化函数F1上的误差收敛曲线

进一步，可将OMA应用于复杂工程约束优化问题，例如之前推送的两期算法应用内容：

算法应用：基于DBO算法的工程优化设计(第1期)(含MATLAB代码)

算法应用：工程优化设计(第2期)(含MATLAB代码)

这里以压力容器设计(Pressure vessel design)问题为例，展示OMA求解效果。收敛曲线如图10所示。

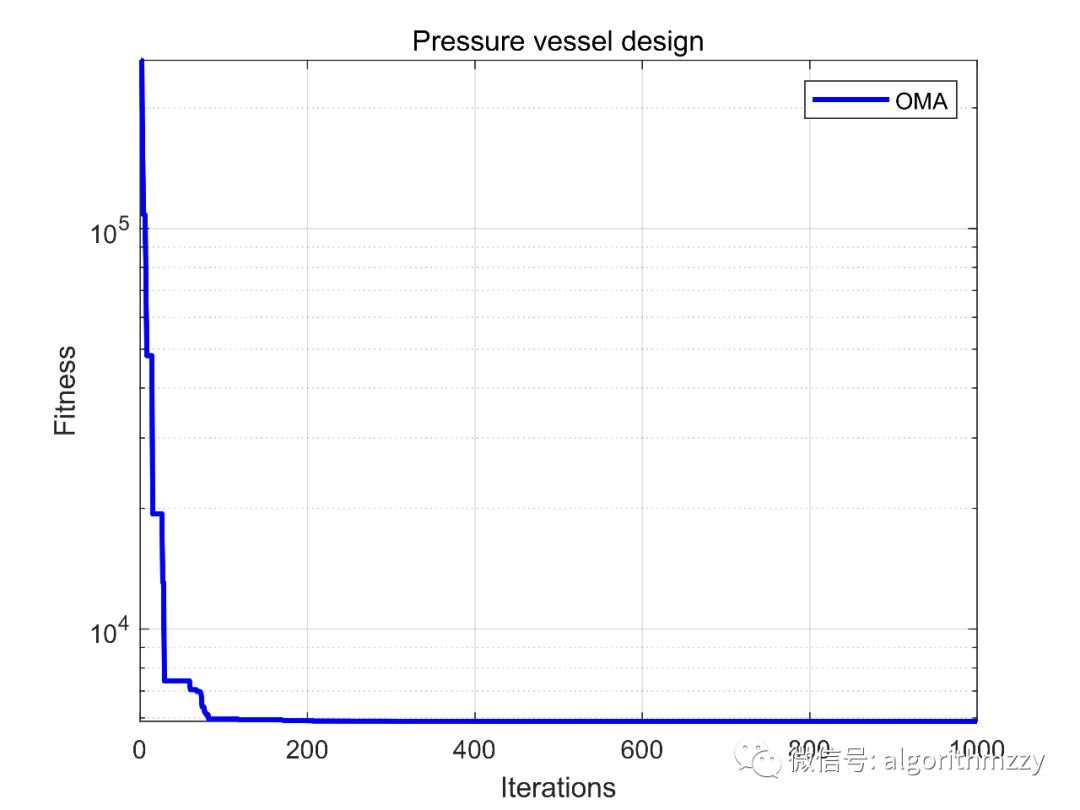
图10 OMA在压力容器设计问题上的目标函数收敛曲线

简单谈一下我的看法：OMA的设计简单，复杂度低，性能中规中矩吧。试了一下，在工程优化问题上的表现还不错。有两点建议：

1.OMA可以选择作为对比算法。本身是刚发表的新算法，并且是KBS上的文章，期刊水平在那里摆着。但OMA的性能又不是很好很好，把自己的算法适当改进一下或许就可以比过。

2.OMA完全也可以作为自己改进的算法。本身很新，性能中规中矩，所以可以改进的地方很多，不像一些算法都改不动了。你完全可以尝试把其他算法的改进策略用到OMA上去看效果。另外就是OMA的灵感来源我觉得还算新颖，里面的常数都取自显微镜设备上的实际数值，设计还是比较合理的，不是强行套。所以可以尝试做一做工作。

05
MATLAB代码

OMA跑CEC2005测试集

关注公众号：启发式算法讨论

OMA跑CEC2013测试集：
关注公众号：启发式算法讨论

OMA跑CEC2014测试集：
关注公众号：启发式算法讨论

OMA跑CEC2017测试集：

关注公众号：启发式算法讨论

OMA跑CEC2020优化函数测试集：

关注公众号：启发式算法讨论

OMA跑CEC2022优化函数测试集：

关注公众号：启发式算法讨论

OMA的勘探(Exploration)和开发(Exploitation)占比分析：

关注公众号：启发式算法讨论

OMA的工程应用(第1期)：压力容器设计、滚动轴承设计、拉伸/压缩弹簧设计、悬臂梁设计、轮系设计、三杆桁架设计。

关注公众号：启发式算法讨论

OMA的工程应用(第2期)：焊接梁设计、多盘离合器制动器设计问题、步进圆锥滑轮问题、减速机设计问题、行星轮系设计优化问题、机器人夹持器问题。

关注公众号：启发式算法讨论

可通过下方链接下载代码清单，在里面寻找需要的算法代码，然后去对应的链接获取。清单会同步更新，一旦有新的代码，就可以在清单里找到。清单里面有部分代码是开源获取的。可随时免费下载。

链接：https://pan.baidu.com/s/1SFDMplrL7tiqGZlrpOSGYg
提取码：8023