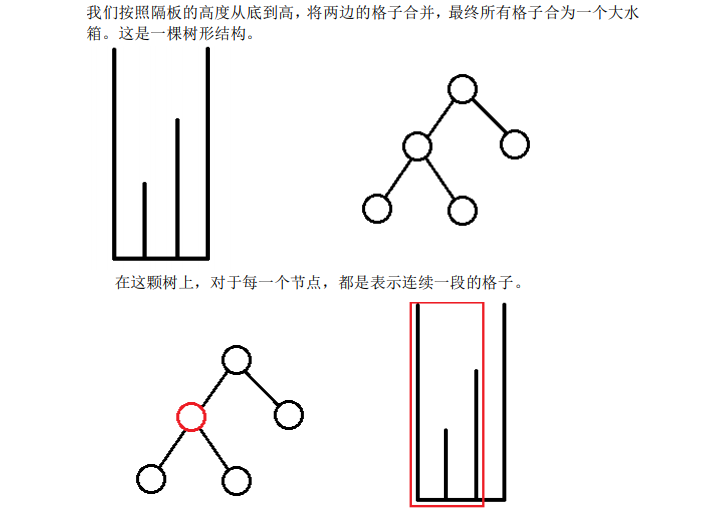
Loj #3085. 「GXOI / GZOI2019」特技飞行
题目描述
公元 \(9012\) 年,Z 市的航空基地计划举行一场特技飞行表演。表演的场地可以看作一个二维平面直角坐标系,其中横坐标代表着水平位置,纵坐标代表着飞行高度。
在最初的计划中,这 \(n\) 架飞机首先会飞行到起点 \(x = x_{st}\) 处,其中第 \(i\) 架飞机在起点处的高度为 \(y_{i,0}\)。它们的目标是终点 \(x = x_{ed}\) 处,其中第 \(i\) 架飞机在终点处的高度应为 \(y_{i,1}\)。因此,每架飞机可以看作坐标系中的一个点,它的航线是从 \((x_{st},y_{i,0})\) 出发、到 \((x_{ed},y_{i,1})\) 结束的一条线段,如下图所示。
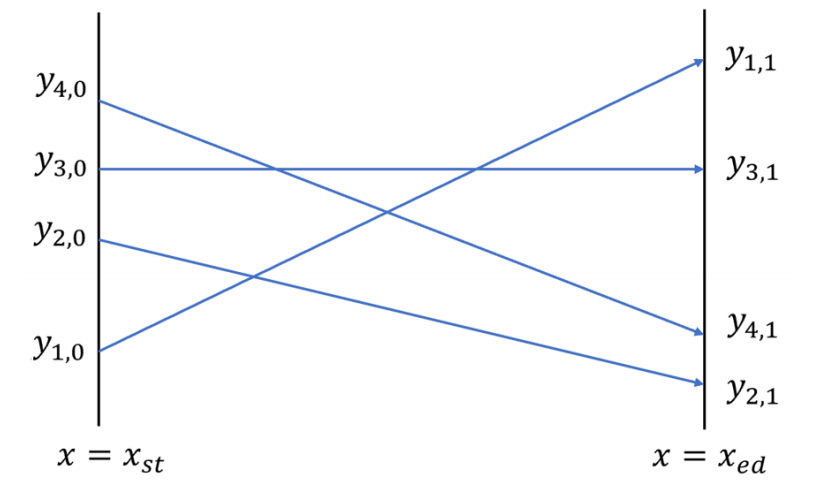
这 \(n\) 架飞机同时出发且始终保持一定的对地速度。因此,对于任意两条交叉的航线(线段),对应的两架飞机必然会同时到达交点处——这就是它们进行特技表演的时刻。它们将会偏转机翼,展现以极近的距离「擦身而过」特技,然后继续保持各自的航线。
航空基地最近还研究了一种新的特技「对向交换」。当两架飞机到达交点处时,之前正在下降的那架立即转为执行抬升动作,之前正在上升的那架则执行一次空翻,两架飞机一上一下、机腹对机腹,同样以极近的距离经过交点,然后互相交换接下来的航线。
我们不必关心特技动作在物理上究竟是如何实现的,飞机仍然看作一个点,在两种特技动作下,航线的变化如下图所示(\(y_{i,1}'\) 表示交换航线后第 \(i\) 架飞机在终点的新高度)。容易发现,「对向交换」会使它们的航线变为折线,并保持它们在纵坐标上的相对顺序;而「擦身而过」会改变它们在纵坐标上的相对顺序。
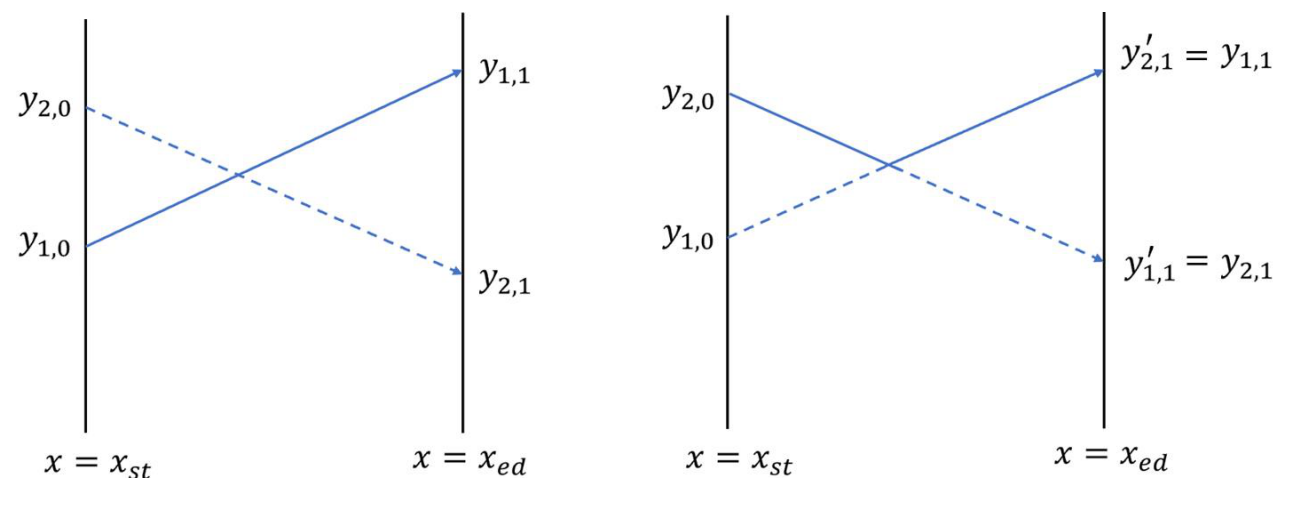
现在,观看表演的嘉宾团提出了一个苛刻的要求——在终点 \(x = x_{ed}\) 处,按照高度排序,\(n\) 架飞机的相对顺序必须与 \(x = x_{st}\) 处的相对顺序一致。嘉宾团还给「对向交换」特技和「擦身而过」特技分别评定了难度系数 \(a\) 和 \(b\),每次「对向交换」特技可以获得 \(a\) 的分数,每次「擦身而过」特技可以获得 \(b\) 的分数。
除此以外,嘉宾团共有 \(k\) 名成员,第 \(i\) 名成员会乘热气球停留在位置 \((p_i,q_i)\) 处,具有 \(r_i\) 的观测距离,可以观测到区域 \(|x - p_i| + |y - q_i| \le r_i\) 里的所有特技。
若某个交点处的特技被一名或多名嘉宾观测到,则可以获得 \(c\) 的额外加分。
注意:特技无论是否被观测到,均可以获得 \(a\) 或者 \(b\) 的得分。
下图是对本题第一幅图 \(4\) 条航线 \(4\) 个交点的一种满足要求的安排,包括 \(2\) 次「对向交换」、\(2\) 次「擦身而过」,\(3\) 项特技被观测到,得分 \(2a + 2b + 3c\)。为了方便观察,图中展现「对向交换」特技的交点稍稍有些分离。
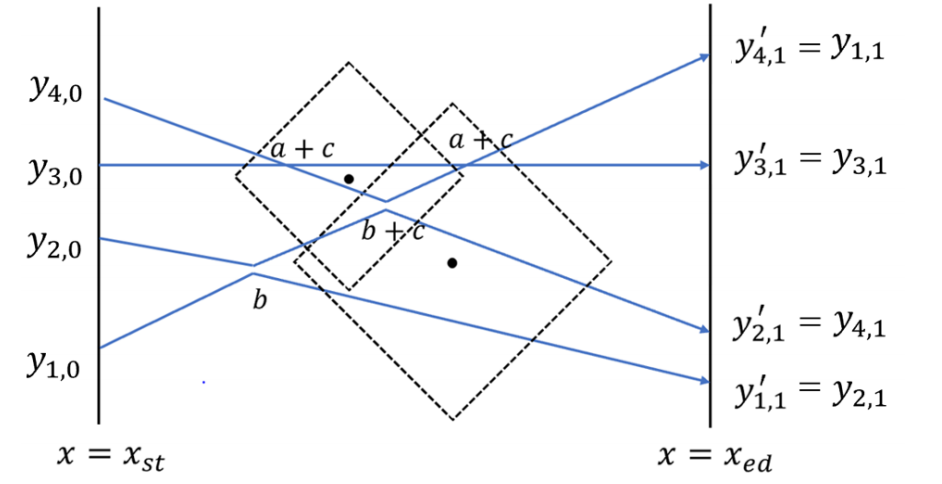
在这次的剧情里,你成为了 Z 市航空基地的规划员,你可以决定在每个交点处是执行「对向交换」还是「擦身而过」。你被要求在保证嘉宾团要求的前提下,计算整个特技表演的可能得到的最低和最高分数。
输入格式
第一行包含六个非负整数 \(n,a,b,c,x_{st},x_{ed}\),分别表示航线(线段)总数、「对向交换」特技的得分、「擦身而过」特技的得分、观测对表演的额外分、飞行起点的横坐标、飞行终点的横坐标。
第二行包含 \(n\) 个非负整数 \(y_{i,0}\),其中第 \(i\) 个数表示第 \(i\) 条航线起点的纵坐标,保证按照从低到高的顺序给出,即 \(y_{i,0} < y_{i + 1,0}\)。
第三行包含 \(n\) 个非负整数 \(y_{i,1}\),其中第 \(i\) 个数表示第 \(i\) 条航线终点的纵坐标。
第四行包含一个非负整数 \(k\),表示嘉宾的数量。
接下来 \(k\) 行每行三个非负整数 \(p_i,q_i,r_i\),分别表示第 \(i\) 名嘉宾所在位置的横、纵坐标与观测距离。
输入数据对于所有航线(线段)在直线 \(x = x_{st}\) 和 \(x = x_{ed}\) 之间的交点总数也有一些限制,详见「数据范围与提示」。
输出格式
输出只有一行,包含两个整数,表示整个特技飞行表演的可能得到的最低和最高分数,中间用一个空格隔开。
数据范围与提示
不存在三条或三条以上的线段交于同一点。
所有坐标和 \(r_i\) 均为 \(5 \times 10^7\) 以内的非负整数。
\(y_{i,0} < y_{i + 1,0}\),\(y_{i,1}\) 各不相同。
\(x_{st} < p_i < x_{ed},1 ≤ a,b,c ≤ 10^3\)。
\(n,k\leq 100,000\),交点数\(\leq 500,000\)。
\(\\\)
\(c\)对答案的贡献可以旋转坐标系过后扫描线解决。
考虑最大和最小的答案一定是其中一个最大化\(a\)的数量,另外一个最小化\(a\)的数量。\(a\)的最大值就是逆序对(交点)个数(虽然为啥我也不知道);最小值很显然,将这个序列看做一个置换,那么答案就是\(n-\)循环节个数。
代码:
#include<bits/stdc++.h>
#define ll long long
#define N 500005
#define eps 1e-9using namespace std;
inline int Get() {int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}while('0'<=ch&&ch<='9') {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}return x*f;}int n;
ll a,b,c,st,ed;
int k;
ll Y0[N],Y1[N];
ll x[N],y[N];
long double d[N];
int rk[N],t[N];
bool cmp(int a,int b) {return Y1[a]<Y1[b];}
struct point {long double x,y;point() {}point(long double _x,long double _y) {x=_x,y=_y;}bool operator <(const point &a)const {if(fabs(x-a.x)>1e-7) return x<a.x;return y<a.y;}
}p[N];
int ptot;
void Get_point(int a,int b) {long double L=abs(Y0[a]-Y0[b]),R=abs(Y1[a]-Y1[b]);long double K=L/(L+R);long double x=1.0*st+(ed-st)*K,y=1.0*Y0[a]+(Y1[a]-Y0[a])*K;p[++ptot]=point(x-y,x+y);
}struct Line {double x;int y1,y2,flag;Line() {}Line(double _x,int _y1,int _y2,int _flag) {x=_x,y1=_y1,y2=_y2,flag=_flag;}bool operator <(const Line &a)const {if(fabs(a.x-x)>eps) return x<a.x;return flag<a.flag;}
}L[N<<2];
int ltot;
int cal1() {static bool vis[N];int cnt=0;for(int i=1;i<=n;i++) {if(vis[i]) continue ;cnt++;for(int j=i;!vis[j];j=rk[j]) vis[j]=1;}return cnt;
}ll ans0,ans1;
int low(int i) {return i&(-i);}
int tem[N<<3];
int m;
void add(int v,int f) {for(int i=v;i<=m;i+=low(i)) tem[i]+=f;}
void add(int l,int r,int f) {add(l,f),add(r+1,-f);}
int query(int v) {int ans=0;for(int i=v;i;i-=low(i)) ans+=tem[i];return ans;
}
void discrete() {static long double py[N<<3];static int ty;ty=0;for(int i=1;i<=ptot;i++) py[++ty]=p[i].y;for(int i=1;i<=k;i++) py[++ty]=y[i]+d[i],py[++ty]=y[i]-d[i];sort(py+1,py+1+ty);int dy=unique(py+1,py+1+ty)-py-1;m=dy;for(int i=1;i<=ptot;i++) {L[++ltot]=Line(p[i].x,lower_bound(py+1,py+1+dy,p[i].y)-py,0,1);if(fabs(py[L[ltot].y1]-p[i].y)>eps) exit(-1);}for(int i=1;i<=k;i++) {int y1=lower_bound(py+1,py+1+dy,y[i]-d[i])-py,y2=lower_bound(py+1,py+1+dy,y[i]+d[i])-py;L[++ltot]=Line(x[i]-d[i],y1,y2,0);L[++ltot]=Line(x[i]+d[i],y1,y2,3);}
}int cal2() {sort(L+1,L+1+ltot);int ans=0;for(int i=1;i<=ltot;i++) {if(L[i].flag==0) {add(L[i].y1,L[i].y2,1);} else if(L[i].flag==1) {if(query(L[i].y1)) ans++;} else {add(L[i].y1,L[i].y2,-1);}}return ans;
}
int main() {n=Get(),a=Get(),b=Get(),c=Get(),st=Get(),ed=Get();for(int i=1;i<=n;i++) Y0[i]=Get();for(int i=1;i<=n;i++) Y1[i]=Get();for(int i=1;i<=n;i++) t[i]=i;sort(t+1,t+1+n,cmp);for(int i=1;i<=n;i++) rk[t[i]]=i;for(int i=1;i<=n;i++) t[i]=0;for(int i=1;i<=n;i++) {t[i]=i;int j=i;while(j>1&&rk[t[j-1]]>rk[t[j]]) {Get_point(t[j-1],t[j]);swap(t[j-1],t[j]);j--;}}sort(p+1,p+1+ptot);k=Get();for(int i=1;i<=k;i++) {x[i]=Get(),y[i]=Get(),d[i]=Get();ll X=x[i]-y[i],Y=x[i]+y[i];x[i]=X,y[i]=Y;}ll cnt=n-cal1();ans0=cnt*a+(ptot-cnt)*b;ans1=ptot*a;ll sp=0;for(int i=1;i<=ptot;i++) {long double X=p[i].x-p[i].y,Y=p[i].x+p[i].y;for(int j=1;j<=k;j++) {if(fabs(p[i].x-1.0*x[j])<=d[j]&&fabs(p[i].y-1.0*y[j])<=d[j]) {sp++;break;}}}discrete();int watch=cal2();ans0+=watch*c,ans1+=watch*c;if(ans0>ans1) swap(ans0,ans1);cout<<ans0<<" "<<ans1;return 0;
}