本文主要是介绍算法系列之七:爱因斯坦的思考题(上) .,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
这是一个很有趣的逻辑推理题,传说是爱因斯坦提出来的,他宣称世界上只有2%的人能解出这个题目,传说不一定属实,但是这个推理题还是很有意思的。题目是这样的,据说有五个不同颜色的房间排成一排,每个房间里分别住着一个不同国籍的人,每个人都喝一种特定品牌的饮料,抽一种特定品牌的烟,养一种宠物,没有任意两个人抽相同品牌的香烟,或喝相同品牌的饮料,或养相同的宠物,问题是谁在养鱼作为宠物?为了寻找答案,爱因斯坦给出了十五条线索:
(1)、英国人住在红色的房子里;
(2)、瑞典人养狗作为宠物;
(3)、丹麦人喝茶;
(4)、绿房子紧挨着白房子,在白房子的左边;
(5)、绿房子的主人喝咖啡;
(6)、抽Pall Mall牌香烟的人养鸟;
(7)、黄色房子里的人抽Dunhill牌香烟;
(8)、住在中间那个房子里的人喝牛奶;
(9)、挪威人住在第一个房子里面;
(10)、抽Blends牌香烟的人和养猫的人相邻;
(11)、养马的人和抽Dunhill牌香烟的人相邻;
(12)、抽BlueMaster牌香烟的人和啤酒;
(13)、德国人抽Prince牌香烟;
(14)、挪威人和住在蓝房子的人相邻;
(15)、抽Blends牌香烟的人和喝矿泉水的人相邻。
这个题目的答案就包含在5个种类共25个元素的所有组合当中,当某一个组合能够满足以上15条线索时,就可以从中找到答案,以下就是一个满足全部线索的组合,可以看出本题的答案是住在绿色房子中的德国人养鱼作为宠物:
| 房子 | 国家 | 饮料 | 宠物 | 烟 |
| 黄色 | 挪威 | 水 | 猫 | Dunhill |
| 蓝色 | 丹麦 | 茶 | 马 | Blends |
| 红色 | 英国 | 牛奶 | 鸟 | PallMall |
| 绿色 | 德国 | 咖啡 | 鱼 | Prince |
| 白色 | 瑞士 | 啤酒 | 狗 | BlueMaster |
用计算机解决这个问题的本质就是枚举这5个种类25个元素的所有组合,应用15条线索对每个组合进行判断,能够满足全部线索的组合就是最终的结果。和其它用穷举法算法一样,解决这个推理题也需要解决三个关键点:定义能够描述这个问题的数据模型、基于这个数据模型的一套枚举算法和应用15条线索判断结果是否正确的方法。
考察这个问题的描述,需要枚举结果的元素分为5个类别,分别是房子(颜色)、国家、饮料类型、宠物种类和香烟的品牌。根据题意,5个种类的元素不能重复,但是彼此存在联系,这个联系简单描述就是:某个国家的人只能住在某个颜色的房子中,喝一种饮料,养一种宠物并抽一种品牌的香烟。定义数据模型时可以采用“组”(group)的概念来定义这种关系,每个“组”包含5个种类的各一个元素,保证了对上述固定关系的约束。每个元素都由两个属性,一个是类型,一个是值,比如“咖啡”,其类型是饮料,值是咖啡,可以这样对元素进行定义:
| 61 typedef struct tagItem 62 { 63 ITEM_TYPE type; 64 int value; 65 }ITEM; |
确定了元素的数据定义,“组”的数据定义就可以确定了:
| 107 typedef struct tagGroup 108 { 109 ITEM items[GROUPS_ITEMS]; 110 }GROUP; |
这个GROUP的数据定义虽然清晰明了,但是对GROUP内的元素的定位不是很直观,比如对GROUP内的某个元素操作时需要遍历所有的元素逐个比较类型来定位元素,这就存在一个算法的效率问题。既然GROUP内的item用数组进行组织,而数组的下标天生就具有位置关系,何不利用这一点简化数据定义呢?首先对ITEM_TYPE的值进行一些约束,为每个类型赋一个明确的值,这个值就是item数据的位置,固定了值之后的ITEM_TYPE定义如下:
| 42 typedef enum tagItemType 43 { 44 type_house = 0, 45 type_nation = 1, 46 type_drink = 2, 47 type_pet = 3, 48 type_cigaret = 4 49 }ITEM_TYPE; |
对GROUP也重新定义:
| 107 typedef struct tagGroup 108 { 109 int itemValue[GROUPS_ITEMS]; 110 }GROUP; |
这样定义GROUP可以显著简化数据定位问题,比如“住在中间那个房子里的人喝牛奶”这个线索,就可以这样用代码实现:
| groups[2].itemValue[type_drink] = DRINK_MILK; |
接下来要处理15条线索的数学模型问题。先分析一下这15条线索,大致可以分成三类:第一类是描述某些元素之间具有固定绑定关系的线索,比如,“丹麦人喝茶”和“住绿房子的人喝咖啡”等等,线索1、2、3、5、6、7、12、13可归为此类;第二类是描述某些元素类型所在的“组”所具有的相邻关系的线索,比如,“养马的人和抽Dunhill牌香烟的人相邻”和“抽Blends牌香烟的人和养猫的人相邻”等等,线索10、11、14、15可归为此类;第三类就是不能描述元素之间固定关系或关系比较弱的线索,比如,“绿房子紧挨着白房子,在白房子的左边”和“住在中间那个房子里的人喝牛奶”等等。
对于第一类具有绑定关系的线索,其数学模型可以这样定义:
| 67 typedef struct tagBind 68 { 69 ITEM_TYPE first_type; 70 int first_val; 71 ITEM_TYPE second_type; 72 int second_val; 73 }BIND; |
first_type和first_val是一个绑定关系中前一个元素的类型和值,second_type和second_val是绑定关系中后一个元素的类型和值。以线索6“绿房子的主人喝咖啡”为例,first_type就是type_house,first_val就是COLOR_GREEN(COLOR_GREEN是个整数型常量),second_type就是type_drink,second_val就是DRINK_COFFEE(DRINK_COFFEE是个整数型常量)。线索1、2、3、5、6、7、12、13就可以存储在binds数组中:
| 75 const BIND binds[] = 76 { 77 { type_house, COLOR_RED, type_nation, NATION_ENGLAND }, 78 { type_nation, NATION_SWEDEND, type_pet, PET_DOG }, 79 { type_nation, NATION_DANMARK, type_drink, DRINK_TEA }, 80 { type_house, COLOR_GREEN, type_drink, DRINK_COFFEE }, 81 { type_cigaret, CIGARET_PALLMALL, type_pet, PET_BIRD }, 82 { type_house, COLOR_YELLOW, type_cigaret, CIGARET_DUNHILL }, 83 { type_cigaret, CIGARET_BLUEMASTER, type_drink, DRINK_BEER }, 84 { type_nation, NATION_GERMANY, type_cigaret, CIGARET_PRINCE } 85 }; |
对于第二类描述元素所在的“组”具有相邻关系的线索,其数学模型可以这样定义:
| 89 typedef struct tagRelation 90 { 91 ITEM_TYPE type; 92 int val; 93 ITEM_TYPE relation_type; 94 int relation_val; 95 }RELATION; |
type和val是某个“组”内的某个元素的类型和值,relation_type和relation_val是与该元素所在的“组”相邻的“组”中与之有关系的元素的类型和值。以线索10“抽Blends牌香烟的人和养猫的人相邻”为例,type就是type_cigaret,val就是CIGARET_BLENDS(CIGARET_BLENDS是个整数型常量),relation_type是type_pet,relation_val是PET_CAT(PET_CAT是个整数型常量)。线索10、11、14、15就可以存储在relations数组中:
| 097 const RELATION relations[] = 098 { 099 { type_cigaret, CIGARET_BLENDS, type_pet, PET_CAT }, 100 { type_pet, PET_HORSE, type_cigaret, CIGARET_DUNHILL }, 101 { type_nation, NATION_NORWAY, type_house, COLOR_BLUE }, 102 { type_cigaret, CIGARET_BLENDS, type_drink, DRINK_WATER } 103 }; |
对于第三类线索,无法建立统一的数学模型,只能在枚举算法进行过程中直接使用它们过滤掉一些不符合条件的组合结果。比如线索8“住在中间那个房子里的人喝牛奶”,就是对每个饮料类型组合结果直接判断groups[2].itemValue[type_drink]的值是否等于 DRINK_MILK,如果不满足这个线索就不再继续下一个元素类型的枚举。再比如线索4“绿房子紧挨着白房子,在白房子的左边”,就是在对房子类型进行组合排列时,将绿房子和白房子看成一个整体进行排列组合的枚举,得到的结果直接符合了线索4的要求。
解决了数据模型的定义,接下来就要考虑如何判定一个组合结果符合题目要求的全部线索。这个判别是关键点,如果不能正确地从上亿个组合结果中识别出正确的结果,后面将要介绍的枚举算法就成了无的放失。根据本文建立的数学模型,第三类线索直接在枚举算法部分应用,因此只需要对枚举得到的组合结果应用第一类线索和第二类线索进行过滤即可。
具有绑定关系的线索描述的是一个“组”内两种元素之间的固定关系,判断的方法就是遍历全部的“组”,找到BIND数据中的first_type和first_val标识的元素所在的组group,然后检查group组中类型为second_type的元素的值是否等于second_val,如果group中类型为second_type对应元素的值与second_val的值不一致就直接返回检查失败,否则就说明当前的组合结果满足此BIND数据对应的线索,然后对下一个BIND数据重复上述检查过程,直到检查完binds数组中所有线索对应的BIND数据。图(1)是具有绑定关系的线索检查流程图:
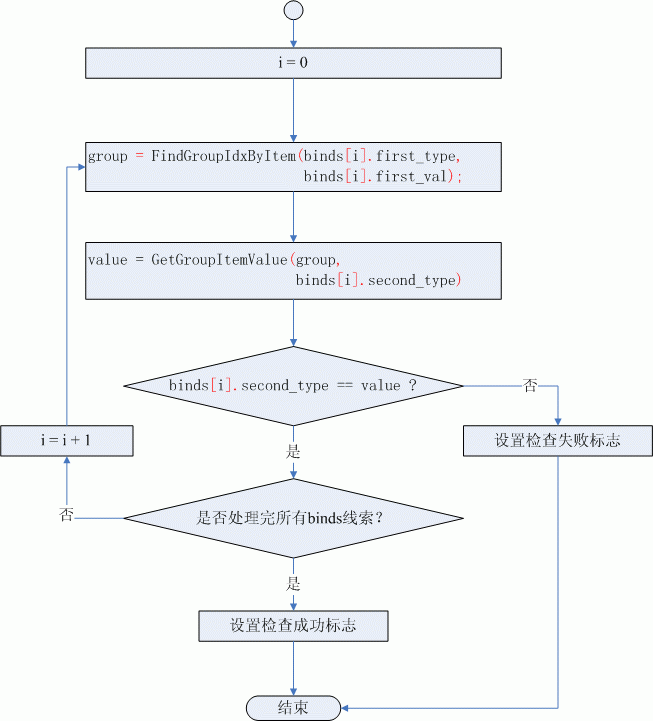
图(1)具有绑定关系的线索检查流程图
“组”相邻关系的线索描述的是相邻的两个组之间元素的固定关系,判断的方法就是遍历全部的“组”,找到RELATION数据中的type和val标识的元素所在的组group,然后分别检查与group相邻的两个组(第一个组和最后一个组只有一个相邻的组)中类型为relation_type的元素对应的值是否等于relation_val,如果相邻的组中没有一个能满足RELATION数据就表示当前组合结果不满足线索,直接返回检查失败。相邻的组中只要一个组中的元素满足RELATION数据描述的关系就表示当前组合结果符合RELATION数据对应的线索,需要对下一个RELATION数据重复上述检查过程,直到检查完relations数组中的全部线索对应的RELATION数据。图(2)是具有“组”相邻关系的线索检查流程图:
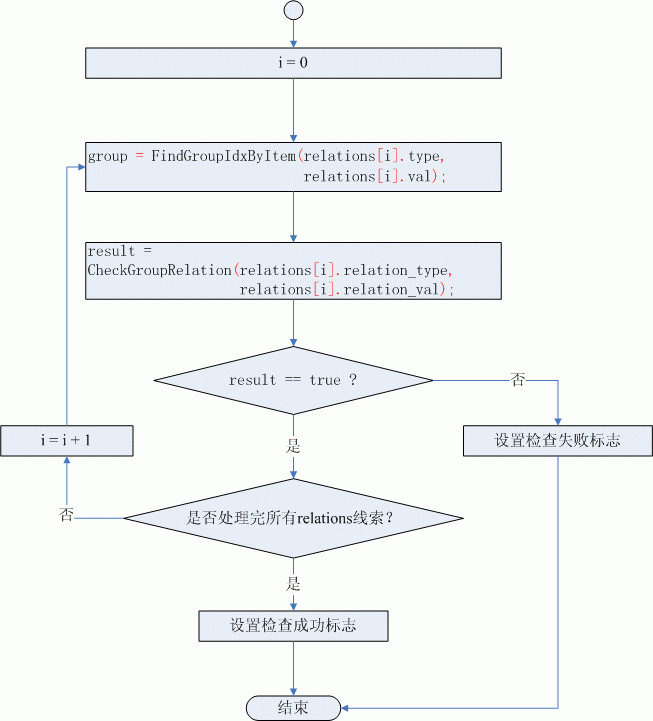
图(2)“组”相邻关系的线索检查流程图
【未完,“算法系列之七:爱因斯坦的思考题(下)”继续】
这篇关于算法系列之七:爱因斯坦的思考题(上) .的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








