牛客编程巅峰赛S2第9场-倔强青铜组C题-牛牛和网格三角形

本文主要是介绍牛客编程巅峰赛S2第9场-倔强青铜组C题-牛牛和网格三角形，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

话说2020年12月15日晚8点，🐮客举行了一场程序猿间的巅峰对决，作为一个菜鸡程序猿的我，为了瞻仰大神们帅气的英姿，偷偷的参加了最强的倔强青铜组的比赛，第一题很简单，第二题不想看，第三题，嘿有意思！
由于当时没有做出来，就冥思苦想，然后看AC的代码，终于功夫不负有心人，终于做出来了！
下面给出题目的描述：

题目描述：

牛牛有一个长和高都为n（1≤n≤10 的10000幂）的网格三角形，牛牛想从从左下角点走到右上角点，但是牛牛只能向上或者向右沿着网格的边走，牛牛想知道从左下角点走到右上角点的方案数的奇偶性。牛牛现在给你n，请你告诉牛牛路径方案数的奇偶性，若是奇数返回true，若是偶数返回false。

示例：

示例图
输入：“5”
输出：false
—————————————华丽的分割线—————————————
初见此题，毫无头绪，再赏一帆，别有风味。
首先我想到了通过递归求解每个n的方案数，然后判断是奇数还是偶数，不过发现n太太大了，求解是不可能的。
然后我进一步想到了动态规划求解。但是n还是太大了，不过当n不是太大的时候，这题可以用动态规划做，也可以通过动态规划求解方案数，同时动态规划也是进一步解决该题的切入点，因此着重讲解动态规划的方法。
首先可以将网格看成二维空间的坐标系，每个点都有一个坐标，因此这道题就可以转换为从(0,0)点到(n,n)点的路径数了。
那路径数应该怎么求呢？
我们首先看整个二维空间下(0,0)点到(n,n)点的路径方案数，因为目标是(n,n)点，并且只能向右和向上走，因此f(n,n)=f(n-1,n)+f(n,n-1),如果不明白可以看下图：
公式求解示意
要到(n,n)点，可以从(n-1,n)点向上走一个单位，也可以从(n,n-1)点向右走一个单位，因此只要知道到达这两点的路径数就可以求出来了。
但是，可是，注意： 因为题中只有一半的空间，所以到(n,n)点的方式只有从(n-1,n)向上走一个单位的方法，因此f(n,n)=f(n-1,n)；
同时我们可以很容易的看出，横坐标为0的点的路径都是1，即f(0,j)=1；
综上我们可以得到关系式如下：

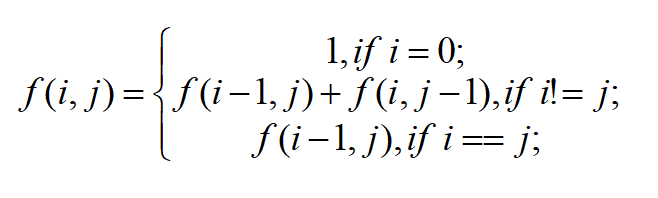
通过实现该公式，即可求出路径数，然后再判断奇偶，代码如下：

    public static int judge (String n) {// write code hereint num = Integer.valueOf(n);int[][] dp = new int[num+1][num+1];for(int i = 0 ; i <= num; i++) {dp[0][i] = 1;}for(int i = 1; i <= num; i++) {for(int j = i; j <= num; j++) {if(i!=j) {dp[i][j] = (dp[i-1][j]+dp[i][j-1])%2;}else {dp[i][j] = dp[i-1][j]%2;}}}return dp[num][num];}

为了计算结果能够保存，我将结果对2取模了，通过动态规划能够解决一部分，但是n是10的10000次方，创建dp数组就很占空间。
那怎么办呢？当然是向大神们学习了啊
通过看AC的大神代码，我发现他们并不是真的求出路径数后判断的，而是通过判断n的二进制码是否含有0来给出结果的。
我看到是一脸懵逼，为什么能够这样就给结果呢？
后来我看到讨论说到，只有当n为2的x次幂减1时，结果才是奇数。
同时看到大神们说通过dp打表得出的规律，为此我通过上面的程序，进行了打表（前32），得到结果如下：
打表图
我勒个去，还真是！
既然知道规律了，那就求解吧！下面首先给出程序代码：

    public boolean judge (String n) {// write code hereBigInteger bigInt = new BigInteger(n);//java中的大数类String str = bigInt.toString(2);//转换成2进制字符串for(int i = 0; i < str.length(); i++) {if(str.charAt(i)=='0') return false;//判断2进制串中是否有0}return true;}