本文主要是介绍废柴日记4:迟到的『构造最小生成树算法』①,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
=================================================
废柴日记4:迟到的『构造最小生成树算法』· 其一
=================================================

=================================================
日期:2021年9月14日 天气:晴
=================================================
其实,我每天都还好。
昨天还一脸自信的样子,嚣张地说着什么 “根本不需要我去想该更新什么内容” 的话,结果迅速打脸,有种吃瘪龙的感觉。

就在博主还在发愁该如何守护日更的誓言,正大光明的水(gan)一篇博客出来的时候,博主突然想起来,我还欠数据结构老师一篇关于普里姆(Prim)算法与克鲁斯卡尔(Kruskal)算法讲解的博客。

那还是一个阳光明媚的下午,当时我们正在机房上实验课,上机的内容正是普里姆(Prim)算法与克鲁斯卡尔(Kruskal)算法。之前也说过,博主的脑回路相较于常人比较的特别,我对于这两个算法的逻辑有着独特的理解方式。
实验课下课之后,我又去找老师讨论一些东西。不知道是怎么了(现在想想就是当时脑子抽了),我突然说了一句:“我感觉我可以把我对这两个算法的理解写成博客,这样的话也可以让更多的人了解到这两个算法还能这么想。”
当时是大二上学期,现在已经是大三了,我也算是拖欠了1年左右。
但是,答应别人的事,无论多晚也要完成,绝对不能辜负这份信任的。
"拉过勾的事情,就一定要做到!"——《星游记》

所以这也算是填坑吧,接下来的几篇『废柴日记』,博主将会用尽毕生所学,尽全力向大家描绘我脑中的『最小生成树』宇宙。
前方高燃,闲人回避。
Ⅰ.概念引入(图,无向图,有向图,网)
首先,在引入最小生成树这一概念之前,我们需要学习它的几个前置知识:
①图:在计算机科学中,图就是一些顶点组成的集合,顶点与顶点之间有边相连,如下图所示。
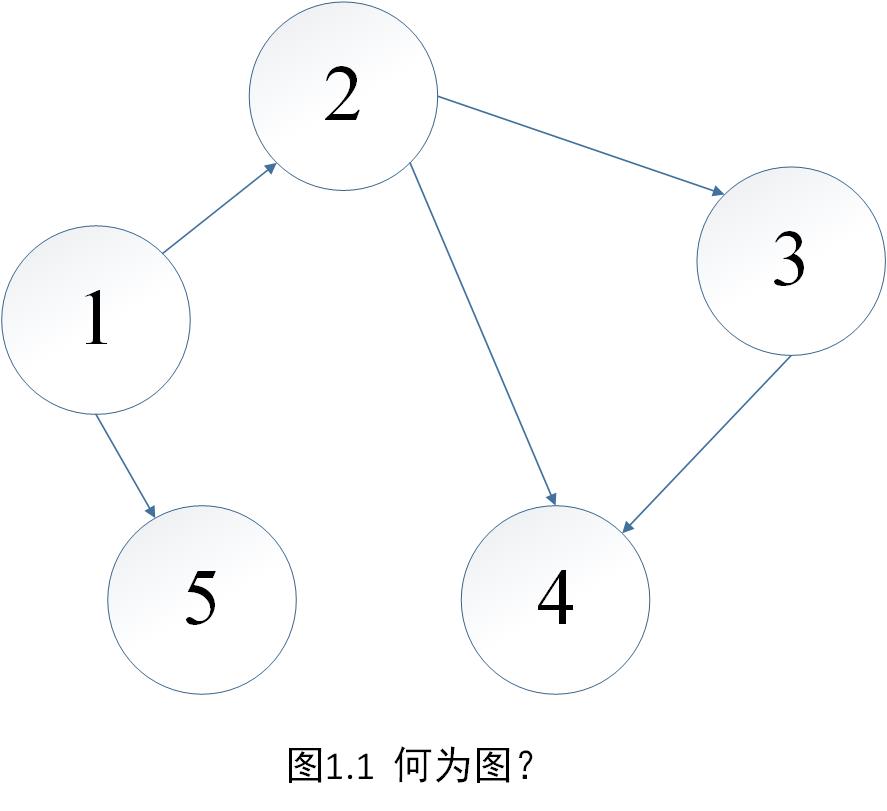
我们将上图命名为图 G ,则在图 G 中共有5个顶点:{1,2,3,4,5},在这5个点之间存在着5条边:{1→2,1→5,2→3,2→4,3→4}。
我们再将由顶点组成的集合{1,2,3,4,5}命名为 V ,由边组成的集合{1→2,1→5,2→3,2→4,3→4}命名为 E ,则图 G 可以表示为:G=(V,E) 。
图的概念非常简单,大家可以联想一下初中时所接触到的几何图形。
(比如一个三角形,它就是由3个顶点与3条边组成的图,只不过我们当时研究的是如何在那个三角形上画一条辅助线然后解一大堆式子才能从老师那里拿到第二问的分数罢了(lll¬ω¬))
②无向图、有向图与网
- 无向边:若顶点 Vi 与顶点 Vj 之间的边没有方向,则称这条边为无向边,并用无序偶对(Vi,Vj)表示。
- 有向边:若顶点 Vi 与顶点 Vj 之间的边有方向,则称这条边为有向边,也可以称之为弧(Arc),我们用有序偶<Vi,Vj>表示。
我们将 Vi 称为弧<Vi,Vj>的弧尾(tail)或初始点(Initial node),将 Vj 称为弧<Vi,Vj>的弧头(head)或终端点(Terminal node)。
<Vi,Vj>代表 Vi、Vj 之间具有一条有向边,方向为 Vi 指向 Vj 。
注意:对于无向边(Vi,Vj),我们可以随意改变其前后的顺序,及(Vj,Vi)与(Vi,Vj)表示的是同一条无向边;而对于有向边<Vi,Vj>,我们不能随意改变其前后的顺序,及<Vi,Vj>表示的是有向边Vi→Vj,而<Vj,Vi>表示的则是有向边Vj→Vi。
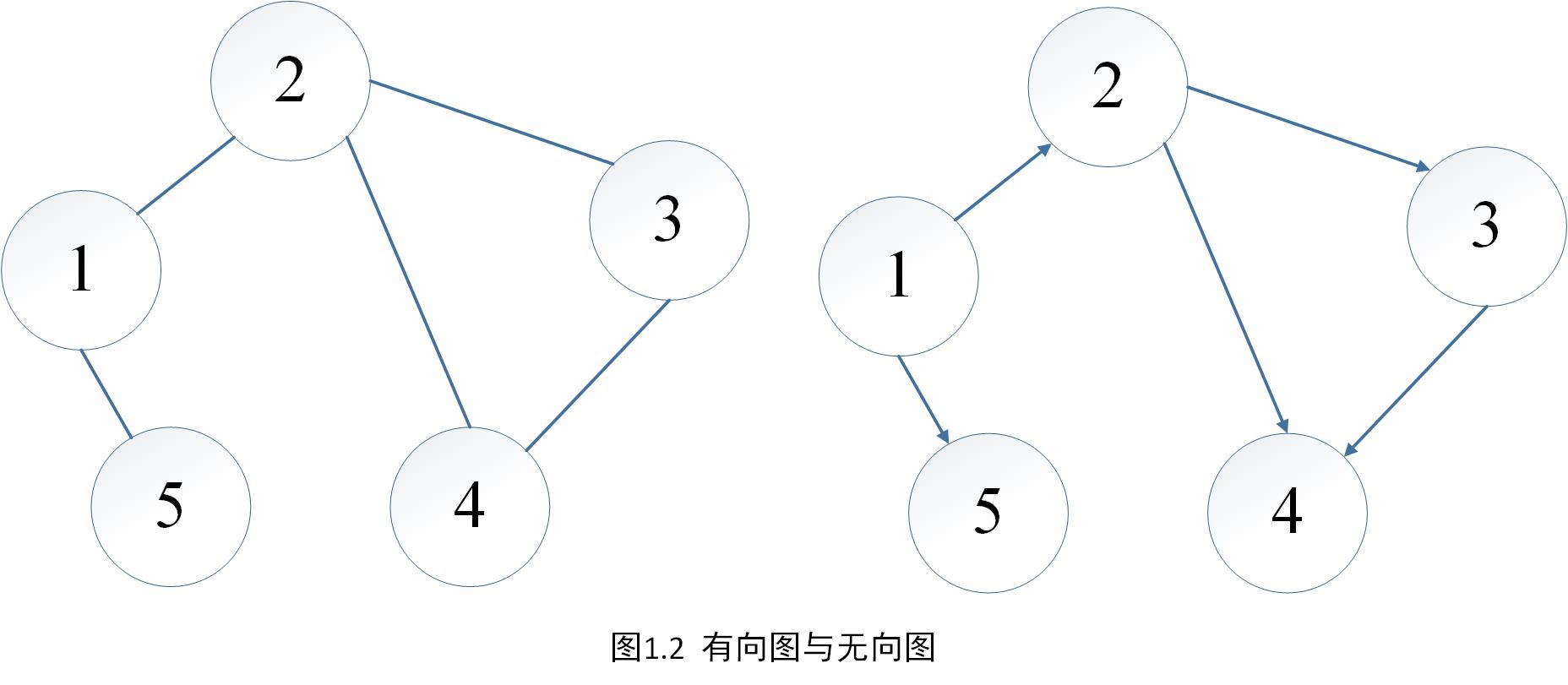
- 无向图:如果图中任意两个顶点之间的边都是无向边,则称该图为无向图(Undirected graphs)。
- 有向图:如果图中任意两个顶点之间的边都是有向边,则称该图为有向图(Directed graphs),图1.1就是一张有向图。
关于无向图与有向图,大家可以联想一下你家到超市的道路与高速公路:
- 从你家到超市假如只有一条路通道A,你从Home出发到达超市所要经过的道路和你从超市回Home所要经过的道路是同一条道路通道A。所以此时通道A是无向的道路。

- 我们假设在城市A与城市B之间有建设高速公路X、Y。当我们从城市A出发前往城市B的时候,我们只能选择高速公路X出发;当我们从城市B返回城市A的时候,我们也只能选择高速公路Y出发。此时高速公路X与高速公路Y就是两个有向的道路。类似的场景还有坐地铁,坐火车等等。
- 网:有些图的边/弧上具有与它相关的数字,我们称这些数字为权(Weight) ,这些权可以表示为从一个顶点到另一个顶点的距离或是耗费。而我们把带权的图称为网(Network)。如图1.5所示的带权有向图就是一张网。
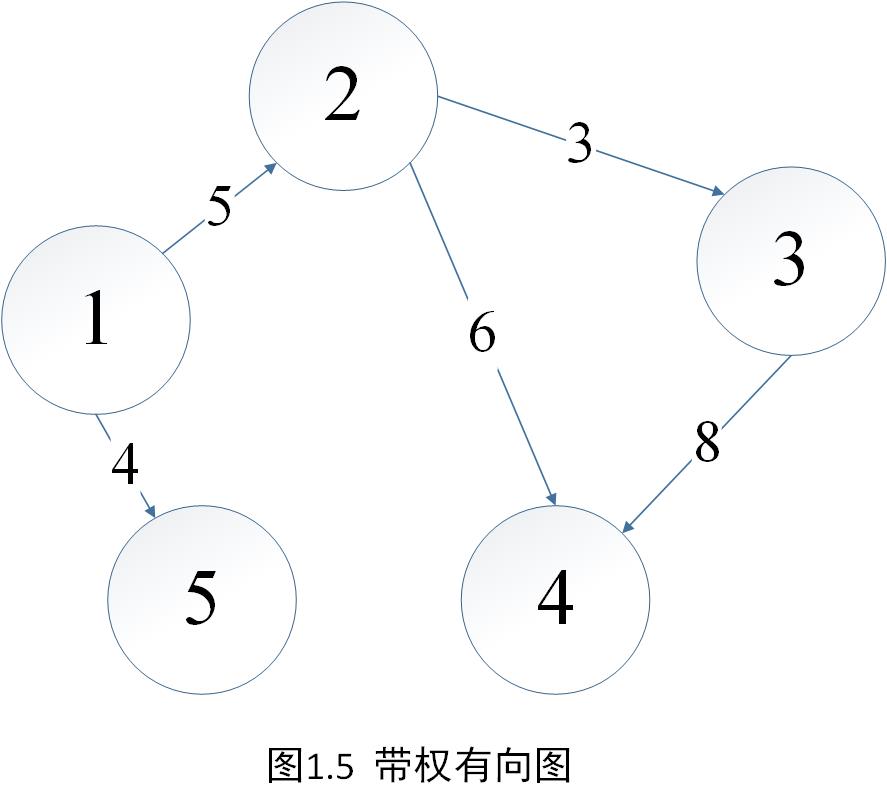
关于网的概念其实也并不难,我们在上面举例时将有向边比作高速公路,在这个比喻之上加上一些实际情况:上高速是要交钱的,而这个权值就代表这条高速公路的收费价格。

Ⅱ.进阶概念(连通,连通图,极大连通子图,极小连通子图)
①连通,连通图
- 连通:在无向图 G 中,如果我们从『顶点 i』出发,中途经过一些边之后可以到达『顶点 j』,我们认为『顶点 i』与『顶点 j』是连通的。
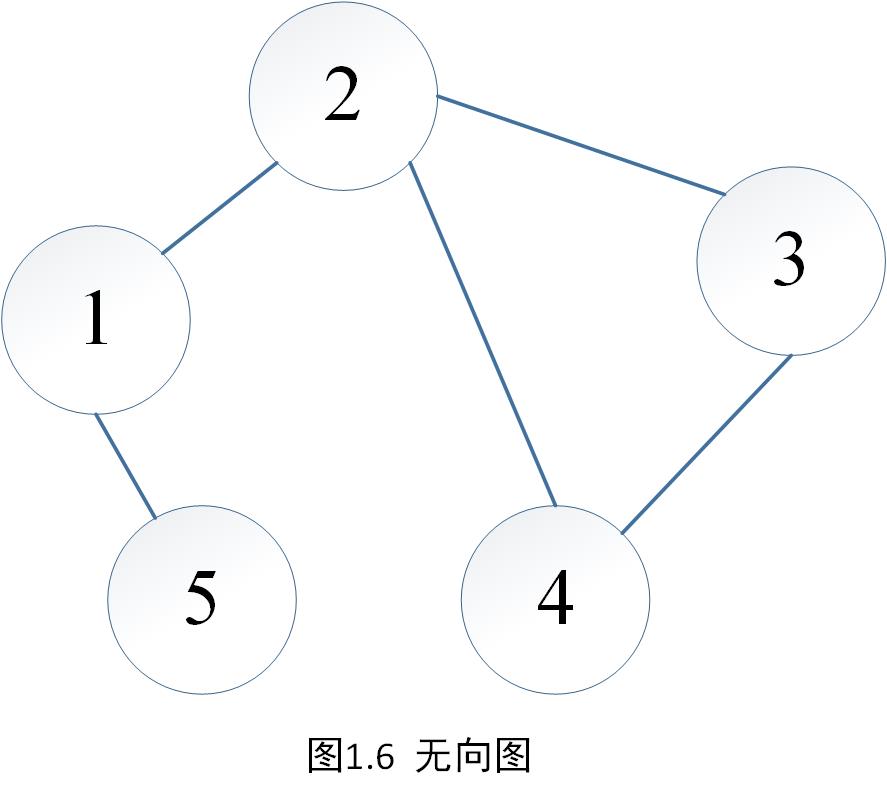
在无向图(图1.6)中,『顶点5』可以经过边<5,1>,<1,2>到达『顶点2』,我们就可以说:『顶点5』与『顶点2』是连通的。
- 连通图:如果在无向图 G 中任意两点都是连通的,我们称这张图为连通图。图1.6就是一张连通图。
连通与连通图的概念是对于无向图而言的,而对于有向图我们还有其他的说法。(有机会再说)
②极大连通子图(又称连通分量),极小连通子图(又称生成树)
- 极大连通子图(又称连通分量):对于无向图G如果满足以下条件,则我们说无向图图G是自身的极大连通子图(或者连通分量)。
- 图G是一张连通图;
- 对于当前的图G来说,如果我们此时在图G加入一个原本不存在的点,会使得图G不再连通;
我们将图1.6中的连通图称为图 G 。
此时,我们现在再向图 G 中加入一个新的顶点——『顶点6』形成图1.7:

现在由于『顶点6』的加入,使得原本连通的图 G 不再满足连通图的条件,破坏了连通的条件。
此时我们称:图 G 是它自身的一张极大连通子图。
- 极小连通子图(又称生成树):对于连通图 G,图 G存在一个子图 G',满足以下条件,我们称子图G'为图G的极小连通子图(又称生成树)。
- 图G'是一张连通图;
- 如果任意删除图G'上的一条边都会使得图G'不再连通;
还是拿图1.6说事,对于图1.6,我们能找到它的一张子图(删去原图的部分点和边):
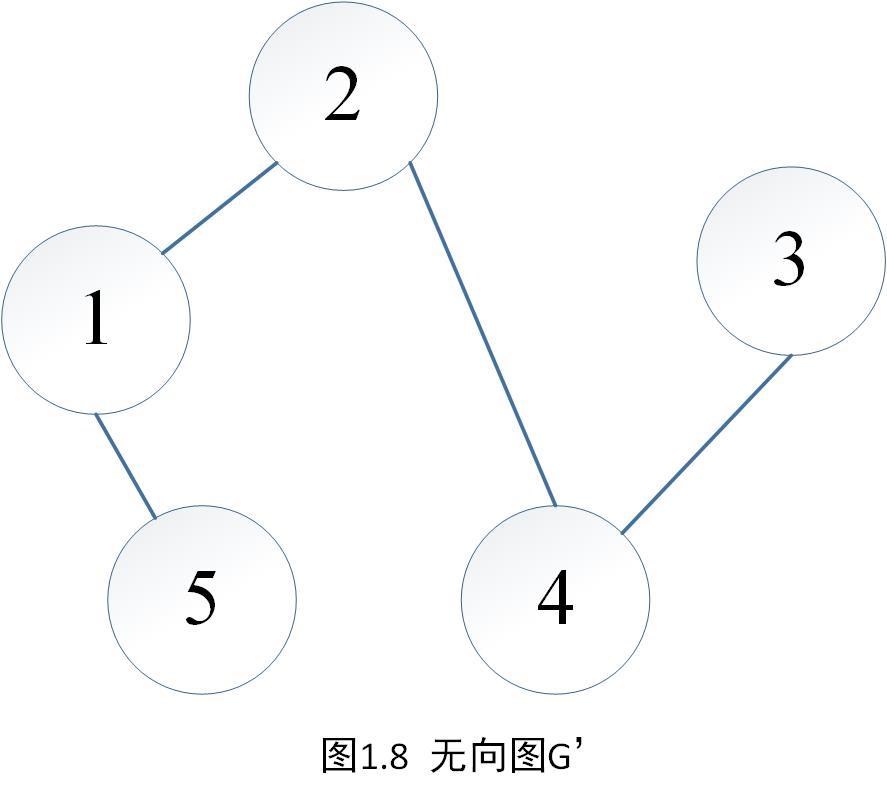
对于这张图G',图G'是一张连通图。并且此时我们发现,我们无论怎么去抹除图G'的边或者点,都会使得结果不再连通,我们说图G'是图G的一张极小连通子图(或者生成树)。
对进阶概念部分做个总结:
- 连通与连通图是基于无向图的概念衍生的。
- 极大连通子图是基于无向图的概念衍生的。(既包含连通图也包含非连通图)
- 极小连通子图是基于连通图的概念衍生的。
- 连通图只有一张极大连通子图,即自身;非连通图有很多张极大连通子图。
- 一张连通图不止一张极小连通子图。
今天就先介绍这些,明天继续,各位晚安~
吾日三省吾身:日更否?刷题否?快乐否?
已更,已刷,快乐滴很!
吾心满意足。

这篇关于废柴日记4:迟到的『构造最小生成树算法』①的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!